Polygonkonstruktionen

(Planimetrie/ Polygonkonstruktionen)

Inhaltsverzeichnis

Einleitung

Viereckskonstruktionen

Inhalt „Polygonkonstruktionen“

Kreiskonstruktionen

Verschiedenes

Einführung

Die Konstruktion von Polygonen hängt nicht nur von der Eckenzahl, sondern auch von den Symmetrien ab. So benötigt man z.B. für die Konstruktion eines Quadrates nur eine Größe (Länge der Seite oder Diagonale), da die große Symmetrie festschreibt, dass a) alle Winkel rechte Winkel sind und b) alle Seiten gleich lang sind. Nimmt man eine Symmetrie weg, z.B. das Rechteck, so dass sich die generelle Unbestimmtheit erhöht (Seiten können verschieden lang sein) so benötigt man bereits zwei Werte. Geht man zum Parallelogramm über (Winkel sind paarweise variabel) , so benötigt man drei Werte u.s.w. Die Zusatzbedingungen, wie z.B. gleiche Werte, sorgen dafür, dass man zusätzliche Werte als ursprünglich gegeben erhält.

Beispiel

Bei einem Dreieck ist nur eine Seite gegeben. Das reicht im allgemeinen Fall nicht für die Konstruktion aus. ist aber noch angegeben, dass es sich um ein gleichseitiges Dreieck handelt, so kann aus den Formeln

α + β + γ = 180°

und

a = b = c (gleichseitig)

die Angabe

α = β = γ = 60°

gewonnen werden. Hier ergeben sich also vier Werte, davon sind drei voneinander unabhängig. Diese Werte reichen für die Konstruktion aus.

Allgemeines Polygon

Ein unregelmäßigen N-Eck ist konstruierbar, wenn:

N-1 Seiten und die dazwischenliegenden N-2 Winkel bekannt sind.

Regelmäßiges Polygon

Animationen

Alternative Konstruktionen (bei gegebenem Umkreis) zu Quadrat, Fünfeck, Achteck und Zehneck sind auf einer Extraseite zu finden.

Dreieck

Das "regelmäßige" Dreieck ist das gleichseitige Dreieck. Zur Konstruktion bei gegebener Seite siehe Konstruktion 1 (SSS) mit dem Sonderfall, dass alle Seiten gleich sind.

Die Konstruktion bei gegebenem Umkreis entspricht weitgehend der Konstruktion des Sechsecks, mit dem Unterschied, dass nur jeder zweite Punkt auf dem Kreis miteinander verbunden wird.

Viereck

Das regelmäßige Viereck ist das Quadrat. Siehe Konstruktion eines Quadrats.

Fünfeck

Fünfeck bei gegebenem Umkreis

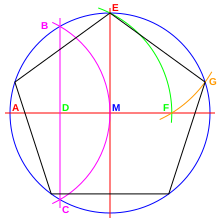
Zeichne einen Kreis (späterer Umkreis, blau) mit Radius r um dem Mittelpunkt M.
Zeichne zwei zueinander senkrechte Durchmesser (rot) ein.
Halbiere einen Radius (magenta, Punkt D).
Zeichne einen Kreis (grün) mit dem Radius DE um Punkt D. Er schneidet die Strecke AM im Punkt F. Die Strecke EF ist die Länge der Seite.
Zum Abtragen auf dem Umkreis einen weiteren Kreisbogen (orange) mit Radius EF um E zeichnen. Er schneidet den ersten Kreis (blau) in G. Vorgang entsprechend wiederholen.

Fünfeck bei gegebener Seitenlänge

Mit Anwendung des goldenen Schnitts, äußere Teilung.

Zeichne eine Strecke AB deren Länge die vorgegebene Seite des Fünfecks ist.
Verlängere die Strecke ab dem Punkt A um ca. drei Viertel der Strecke AB
Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB.
Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB, es ergibt sich der Schnittpunkt F.
Errichte eine Senkrechte zur Strecke AB durch den Punkt F, es ergibt sich der Punkt G
Zeichne eine Parallele zur Strecke FG ab dem Punkt A bis über den Kreisbogen um Punkt A, es ergibt sich der Schnittpunkt H.
Zeichne einen Kreisbogen um den Punkt G mit dem Radius GH bis zur Verlängerung der Strecke AB, es ergibt sich der Schnittpunkt J.
Zeichne einen Kreisbogen um den Punkt B mit dem Radius BJ bis über die Senkrechte die durch den Punkt F geht, es ergeben sich die Schnittpunkte D auf der Senkrechten und E mit dem Kreisbogen um Punkt A.
Zeichne einen Kreisbogen um den Punkt D mit dem Radius BA bis er den Kreisbogen um Punkt B schneidet, es ergibt sich der Schnittpunkt C.
Verbinde die Punkte B-C-D-E-A, somit ergibt sich das Fünfeck.

Wie in der Konstruktion bei gegebenem Umkreis, ist auch hier der Goldene Schnitt der maßgebende Baustein: ${\frac {\overline {BJ}}{\overline {AB}}}={\frac {\overline {AB}}{\overline {AJ}}}=\Phi \approx 1{,}618$

Sechseck

Sechseck bei gegebenem Umkreis

Ein reguläres Sechseck wird konstruiert, indem bei einem Kreis der Radius des Kreises sechsmal auf dem Kreisrand abgetragen wird. Die erhaltenen Punkte sind die Ecken des Sechsecks.

Sechseck bei gegebener Seitenlänge

Konstruktion eines Sechsecks, Seitenlänge gegeben

Ein reguläres Sechseck lässt sich ebenfalls konstruieren, wenn eine vorhandene Strecke als Seitenlänge verwendet werden soll.

Bezeichne die Endpunkte der Strecke mit A bzw. B.
Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB.
Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB, es ergibt sich der Schnittpunkt M, der Mittelpunkt vom späteren Umkreis.
Zeichne einen Kreis um den Punkt M mit dem Radius AM, dies ist der Umkreis des späteren Sechsecks.
Trage die Strecke AB ab dem Punkt B viermal mit dem Zirkel auf dem Umkreis ab.
Verbinde die benachbarten Eckpunkte miteinander, somit ergibt sich das Sechseck ABCDEF

Siebeneck

Nur mit Zirkel und Lineal kann das Siebeneck nicht exakt konstruiert werden. Es gibt jedoch Näherungen.

Näherung 1

**Siebeneck**, einfache Näherungskonstruktion mit gegebenem Umkreis bzw. gegebener Seite

Bei gegebenem Umkreis.

Konstruiere das dem Kreis einbeschriebene gleichseitige Dreieck, indem am Kreis der Radius sechsmal abgetragen wird (Sechseck) und jeder zweite Punkt miteinander verbunden wird.
Halbiere eine Dreieckseite, durch verbinden einer Ecke mit dem gegenüberliegenden Punkt auf dem Umkreis. Die halbe Dreieckseite ist eine Näherung für das Siebeneck.

s\approx r\cdot {\frac {1}{2}}{\sqrt {3}}\approx r\cdot 0{,}8660254

Relativer Fehler:

f={\frac {0{,}8660254037844386-0{,}8677674782351162}{0{,}8677674782351162}}\cdot 100\%\approx -0{,}2\%

Bei einem Radius von 1 m ist die Seite 1,7 mm zu kurz.

Als Ergänzung nebenan eine Konstruktion, die zwar vom 1. Punkt der Beschreibung etwas abweicht, aber mit deren 2. Punkt im Wesentlichen übereinstimmt. Sie bedarf deshalb keiner weiteren Erklärung.

Bei gegebener Seitenlänge.

Das Besondere der nebenstehenden Darstellung ist: Sie zeigt alternativ die Umkehrung, nämlich wie aus einer gegebener Seite, mithilfe eines gleichseitigen Dreiecks mit zwei halbierten Seiten, eine Näherung für das Siebeneck entsteht.

Näherung 2

Diese sehr genaue Näherung ist wegen des Aufwands auf einer Extraseite zu finden.

Achteck

Achteck bei gegebenem Umkreis

Konstruiere das zum gegebenen Umkreis gehörende Quadrat, ohne jedoch seine Seiten einzuzeichnen (also nur die Ecken).
Halbiere einen Zentriwinkel und übertrage ihn auf die anderen rechten Winkel.
Verbinde die Ecken.

Achteck bei gegebener Seite

Siehe Achteck.

Neuneck

Nur mit Zirkel und Lineal kann das regelmäßige Neuneck nicht exakt konstruiert werden. Es gibt jedoch Näherungen. Eine sehr genaue Näherung ist wegen des Aufwands auf einer Extraseite zu finden.

Zehneck

Konstruiere ein regelmäßiges Fünfeck, entsprechend der Konstruktion eines regelmäßigen Fünfecks mit Zirkel und Lineal (s.o.).
Ziehe eine Linie von jeder Ecke des Fünfecks durch den Mittelpunkt des Kreises, der in Schritt 1 gemacht wurde, zur anderen Seite des gleichen Kreises.
Die fünf Ecken des Fünfecks legen jede zweite Ecke des Zehnecks fest. Die verbliebenen fünf Ecken sind die Punkte, die durch Schritt 2 auf der anderen Seite des Kreises konstruiert wurden.

Elfeck

Das regelmäßige Elfeck ist als klassische Konstruktion mit Zirkel und Lineal nicht darstellbar. Erlaubt man jedoch ein zusätzliches Hilfsmittel für die Teilung des 90-Grad-Winkels in elf gleich große Winkel, z. B. die archimedische Spirale oder die Quadratrix des Hippias, führt dies zu einer exakten Seitenlänge $a$ des Elfecks.

Eine Exakte Konstruktion mit der Quadratrix des Hippias als zusätzliches Hilfsmittel sowie eine Näherungskonstruktion bei gegebenem Umkreis sind wegen des Platzbedarfs auf einer Extraseite zu finden.

Zwölfeck

Für die Konstruktion eines regelmäßigen Zwölfecks konstruiert man die Ecken des regelmäßigen Sechsecks und halbiert die Zentriwinkel.

Dreizehneck

Nur mit Zirkel und Lineal kann das regelmäßige Dreizehneck nicht exakt konstruiert werden.

Eine Exakte Konstruktion bei gegebenem Umkreis mit Hilfsmittel sowie eine Näherung ist wegen des Platzbedarfs auf einer Extraseite zu finden.

Vierzehneck

Nur mit Zirkel und Lineal kann das regelmäßige Vierzehneck nicht exakt konstruiert werden. Eine Exakte Konstruktion bei gegebenem Umkreis mit Hilfsmittel sowie eine Näherung ist wegen des Platzbedarfs auf einer Extraseite zu finden.

Fünfzehneck

Das regelmäßige Fünfzehneck ist mit Zirkel und Lineal konstruierbar. Die Konstruktionen zu "Bei gegebenem Umkreis" bzw. "Bei gegebener Seitenlänge" sind im Artikel Fünfzehneck beschrieben.

Siebzehneck

Das regelmäßige Siebzehneck ist mit Zirkel und Lineal konstruierbar.

Die Konstruktionen zu "Bei gegebenem Umkreis" bzw. "Bei gegebener Seitenlänge" sind auf einer Extraseite zu finden.

Eigenschaften, Mathematischer Hintergrund u. a. m. ist im Artikel Siebzehneck beschrieben.

257-Eck

Exakte Konstruktion

Eine exakte Konstruktion mit gegebenem Umkreis ist in 257-Eck beschrieben. Ein Zitat aus dem Artikel: "Die praktische Durchführung der Konstruktion ist per Hand kaum möglich, da die Anforderungen an Präzision bei der notwendigen Größe sehr schwer einzuhalten sind."

Näherungskonstruktion der 1. Seite

Da die exakte Konstruktion des 257-Ecks sehr umfangreich ist und nicht übersichtlich dargestellt werden kann, macht es Sinn auch eine pragmatische Lösung darzustellen. Diese Näherung ist wegen des Aufwands auf einer Extraseite zu finden.

Exakte Konstruktion der 1. Seite mit der Quadratrix des Hippias als zusätzliches Hilfsmittel

Erlaubt man jedoch neben Zirkel und Lineal ein zusätzliches Hilfsmittel für die Teilung des 90-Grad-Winkels in n gleich große Winkel, z. B. die archimedische Spirale oder die Quadratrix des Hippias, ist eine gut nachvollziehbare exakte Konstruktion der ersten Ecke E₁ des 257-Ecks darstellbar. Diese Konstruktion ist auf der gleichen Extraseite zu finden.

65537-Eck

Näherungskonstruktion der 1. Seite

Im Folgenden wird die erste Seite als Näherungskonstruktion mit zwei Hauptschritten, in vergrößerter Ansicht, dargestellt. Diese Näherung ist wegen des Aufwands auf einer Extraseite zu finden.

Exakte Konstruktion der 1. Seite mithilfe der Quadratrix des Hippias und GeoGebra als zusätzliche Hilfsmittel