Die Himmelstafel von Tal-Qadi/ Mondzyklen

Kapitelnavigation - Die Himmelstafel von Tal-Qadi

Hauptteil | Exkurs „Tarxien“| Exkurs „Die Plejaden“ | Exkurs „Astronomische Bezugssysteme“ | Exkurs „Mondzyklen“ | Exkurs „Konjunktionen“ | Java-Programm zur Berechnung der ekliptikalen Koordinaten von Mond und Sonne

 

Ein bei Vollmond während einer Mondfinsternis aus dem Kernschatten der Erde tretender Blutmond.

Die Bezeichnung Monat stammt etymologisch von unserem Erdmond ab. Es handelt sich um ein Erbwort, das auf die seit dem 8. Jahrhundert bezeugten althochdeutschen Formen mānōd beziehungsweise mānōth zurückgeht. Diese wiederum stammt vom indoeuropäischen Wort mēnōt ab, das sowohl Monat als auch Mond bedeuten kann.

Mondzyklen

Die zu beobachtende scheinbare Mondbahn kann im Verlauf verschiedener Perioden durch zahlreiche Mondzyklen beschrieben werden. Die kürzesten Zyklen dauern ungefähr einen Monat im Sonnenkalender, sie längeren Mondzyklen können aber auch mehrere Jahre umfassen.

Der Mond hat ähnlich wie die Sonne einen scheinbaren Winkeldurchmesser von ungefähr 30 Bogenminuten beziehungsweise 0,5 Bogengrad. Dies entspricht bei Betrachtung des eigenen Fingers mit ausgestrecktem Arm in etwa einem Viertel der Fingerdicke.

Synodischer Monat

Der synodische Monat ist durch den Verlauf der Elongation des Mondes in Bezug zur Sonne beschrieben.

Der Mond umrundet die Erde ungefähr zwölfmal schneller als die Erde die Sonne und benötigt für einen Umlauf einen Monat. Die einfachste Wahrnehmung des Mondlaufs ergibt sich durch die Beobachtung der Mondphasen beziehungsweise der Elongationen des Mondes. Der synodische Monat (altgriechisch σύνοδος (synodos) = Zusammentreffen) beschreibt die Dauer zwischen zwei gleichen Mondphasen, also von Neumond zu Neumond beziehungsweise von Vollmond zu Vollmond. Hier wird gemeinhin das Zusammentreffen von Neumond und Sonne am Himmel als Referenzzeitpunkt betrachtet. Ein synodischer Monat dauert etwa 29,53 Tage, und zwölf synodische Monate dauern demzufolge rund 354,37 Tage - das sind gut fünfeinhalb Tage weniger als 360. Dieser Zyklus ist dies Basis für die gängigen Mondkalender (Lunarkalender) mit der gegenüber dem am Sonnenjahr orientierten Solarkalender um zirka 11 Tagen kürzeren Jahreslänge. Bei Lunisolarkalendern wird durchschnittlich alle drei Jahre ein dreizehnter synodischer Monat eingeschaltet, damit der Frühlingspunkt der Sonne ungefähr in der gleichen Jahreszeit bleibt.

→ Zur Zahl Zwölf siehe auch Exkurs Zur Zwölf.

Das altägyptische Horusauge als Folge von Rechtecken mit jeweils der Hälfte der Fläche des Vorgängers in einem Rechteck mit dem Flächeninhalt eins.

Deckenrelief im altägyptischen Tempel von Dendera mit der Darstellung von 15 Mondphasen von links (Neumond) nach rechts (Vollmond) mit den Göttern Junit, Sopdet-Tjenenet, Hor-Behdeti, Hathor, Nephthys, Harsiese, Isis, Osiris, Nut, Geb, Tefnut, Schu, Atum und Month. Im Vollmond vor dem Gott des Mondes Thot ist das von ihm geheilte linke Auge („Mondauge“) des Lichtgottes Horus dargestellt.

Die Ägypter haben ihre Kalender nicht mit einer Siebentagewoche, sondern sowohl mit einer Fünftagewoche als auch mit einer Zehntagewoche geführt. Damit besteht ein synodischer Monat auf weniger als einen halben Tag genau aus sechs Fünftagewochen beziehungsweise aus drei Zehntagewochen. Es wird in der Literatur manchmal darauf hingewiesen, dass das Verhältnis der Länge eines synodischen Monats zu dreißig vollen Tagen

${\frac {29,530589{\text{d}}}{30{\text{d}}}}=0,984353$

fast identisch mit dem folgenden Verhältnis ist (siehe auch Horusauge und Heqat in der altägyptischen Geschichte):

${\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+{\frac {1}{32}}+{\frac {1}{64}}$

$={\frac {32}{64}}+{\frac {16}{64}}+{\frac {8}{64}}+{\frac {4}{64}}+{\frac {2}{64}}+{\frac {1}{64}}$

$={\frac {63}{64}}={\frac {2^{6}-1}{2^{6}}}=1-2^{-6}=0,984375$

Die Abweichung der beiden Verhältnisse beträgt nur 0,022 Promille. Erst nach rund 44700 Monaten oder 3700 Jahren hat sich diese Abweichung auf einen Tag aufsummiert.

Die verschiedenen Mondphasen waren für die Menschen schon immer sichtbar und konnten im Laufe eines synodischen Monats verfolgt werden. Es wird davon ausgegangen, dass zum Beispiel auch auf der Himmelsscheibe von Nebra mindestens eine Mondsichel dargestellt ist, eventuell auch der Vollmond und nach dem österreichischen Ur- und Frühgeschichtler Paul Gleirscher zusätzlich das Altlicht des Mondes:

• Verschiedene möglicherweise auf der Himmelsscheibe von Nebra dargestellte Mondphasen
• 
  Ein im Dezember um Mitternacht fast im Zenit stehender, sehr heller Vollmond.
• 
  Ein zunehmender Mond drei Tage nach Neumond beim akronychischen Untergang am westlichen Abendhimmel drei Wochen vor der Tag-und-Nacht-Gleiche im Herbst. Die rötliche Färbung entstand genauso wie bei der untergehenden Sonne durch die Rayleigh-Streuung in der Erdatmosphäre.
• 
  Das Altlicht eines abnehmenden Mondes (Morgenletzt, vier Prozent beleuchtet) beim heliakischen Aufgang am südöstlichen Morgenhimmel der nördlichen Hemisphäre während der bürgerlichen Dämmerung einen Monat nach der Tag-und-Nacht-Gleiche im Herbst mit Erdschein.
• 
  Vollständig rekonstruiertes Modell der bronzenen und mit Gold tauschierten Himmelsscheibe von Nebra.

Siderischer Monat

Der siderische Monat ist durch den Verlauf der ekliptikalen Länge des Mondes in Bezug zum Frühlingspunkt beschrieben.

Es kann also auch die Zeitspanne betrachtet werden, in der der Mond in Bezug auf den Fixsternhimmel entlang der Ekliptik wieder an der gleichen Stelle erscheint. Dies wird üblicherweise an seinem Erscheinen beim Frühlingspunkt festgemacht. Diese Zeitspanne wird siderischer Monat (lateinisch sideris = des Sterns) genannt und beträgt 27,322 Tage. Dies ist auch die Dauer zwischen zwei aufeinanderfolgenden Erscheinungen des Mondes im Goldenen Tor der Ekliptik, da dessen Lage durch Sterne des Fixsternhimmels bestimmt ist.

→ Siehe auch Exkurs Das Goldene Tor der Ekliptik.

Die Einteilung der 360 Bogengrad langen Ekliptik in 28 gleiche Teile ist in der Bronzezeit verbreitet gewesen. Daraus ergibt sich ein grobes Koordinatenraster für die ekliptikale Länge des Mondes.

Auf der Stachelscheibe von Platt aus der Bronzezeit (um 1500 vor Christus) werden die 28 Mondorte der Tage eines Monats beispielsweise durch eine Kreisreihe dargestellt. Die Hohlform diente zur Herstellung von Schmuckscheiben und hat insgesamt sieben konzentrische Kreise. Davon bestehen zwei aus 12 (innen) beziehungsweise aus 28 (außen) gleichmäßig verteilten Mulden. Die zwölf inneren Mulden entsprechen entlang der Ekliptik den 12 Sonnenorten (Monaten) in einem tropischen Jahr beziehungsweise den 12 Jupiterorten (Jahren) in zwölf Jahren. Die 28 äußeren Mulden entsprechen entlang der Ekliptik den 28 Mondorten (respektive Mondhäusern beziehungsweise Mondstationen) und somit den Tagen in einem siderischen Monat. Der große kreisförmige Stachel im Zentrum der Scheibe könnte als Symbol für die Sonne stehen. Auf ihm konnte die Scheibe von unten zentrisch und drehbar gelagert werden. Mit der Scheibe konnte (abgesehen von den erforderlichen siderischen Schaltmonaten) zwölf Jahre lang in täglich wechselnden Kombinationen in den beiden Lochreihen die Lagen von Mond und Jupiter abgelesen und markiert werden. Damit konnte nach einer Einmessung der Ost-West-Richtung zum Beispiel bei der Tag-und-Nacht-Gleiche zur Jupiterrichtung im Frühlingspunkt der gesamte Lebewesenkreis (Zodiak) jederzeit mit dem täglich ein Mondhaus weiterwandernden Mond vollständig bestimmt werden, auch ohne dass der Jupiter sichtbar sein musste. Mit dieser Information ist es dann auch ohne weiteres möglich, das nicht sichtbare Lebewesenzeichen zu bestimmen, in welchem die Sonne sich aufhält.

Im der indischen Astronomie wurden zu diesem Zweck spätestens 500 Jahre danach die 27 Mondhäuser (oder Mondstationen) eingeführt. Da sich die siderische und die synodische Periode um gut zwei Tage unterscheiden, liegen aufeinanderfolgende Neumonde oder Vollmonde in verschiedenen Mondhäusern, nach denen im hinduistischen Lunisolarkalender die Monate benannt werden.

Dieses System wurde etwas später von den Arabern mit 28 Mondhäusern modifiziert. Das erste Mondhaus liegt bei beiden Einteilungen im Frühlingspunkt in der Epoche um Christi Geburt im Kopf des Lammes beziehungsweise des Widders (Aries) bei den nördlich der Ekliptik liegenden Sternen Scheratan und Hamal (indisch Ashvini = die beiden Rosseschirrenden und arabisch aš-šaraṭān = Die beiden Zeichen). Für das zweite Mondhaus folgt der Bauch des Lammes (indisch Bharani = der Wegtragende und arabisch al-buṭayn = das Bäuchlein). Die Plejaden (indisch Krittika und arabisch aṯ-ṯurayyā) im fetten Schwanz des Lammes markieren im Anschluss das dritte Mondhaus. Das vierte Mondhaus ist durch den roten Riesenstern Aldebaran (arabisch al-dabarān = der Nachfolgende, indisch Rohini = der Rötliche) im Sternbild Stier (Taurus) gekennzeichnet.

• Mondstationen
• 
  Die in eine ringförmige Darstellung projizierten 28 Mondhäuser (von 1 bis 28 entgegen dem Uhrzeigersinn) mit den wichtigsten Sternen entlang der Ekliptik (rote gestrichelte Linie zur Epoche J0000.0). Der Beobachter befindet sich auf der Erde im Zentrum der Darstellung. Nach innen werden die südlichen und nach außen die nördlichen ekliptikalen Breiten gemessen. Die scheinbare Mondbahn pendelt zwischen den beiden zur Ekliptikline benachbarten Hilfslinien. Der Abstand der Hilfslinien beträgt senkrecht zur Ekliptiklinie immer fünf Bogengrad und entlang der Ekliptiklinie immer knapp dreizehn Bogengrad. Mit bis zum Nordpol zunehmender geographischer Breite des Beobachtungspunktes können auch noch knapp ein Bogengrad südlichere ekliptikale Breiten von der Mondscheibe erreicht werden, am Südpol auch noch entsprechend nördlichere ekliptikale Breiten.
• 
  Die in Niederösterreich gefundene und aus Sandstein gefertigte Gussform für die Stachelscheibe von Platt.
  Von innen nach außen gibt es sieben konzentrische Kreise, die folgendermaßen zugeordnet werden können:
  - Eine große zentrische Bohrung (im Gußteil eine große stachelartige Erhebung für die Sonne).
  - Zwölf gleichmäßig verteilte kleine Bohrungen (Zodiak mit zwölf Sternzeichen sowie für die Umlaufzeit des Planeten Jupiter in Jahren).
  - Drei äquidistante Kreislinien (die drei inneren Planeten Merkur, Venus und Mars).
  - Achtundzwanzig gleichmäßig verteilte kleine Bohrungen (Mondhäuser).
  - Ein großer abschließender Kreis (Saturn als der Langsame und Beständige).
• 
  Die älteste belegte kreisförmige Struktur in Stonehenge 1 (zirka 3100 bis 2900 vor Christi) besteht aus den 56 Aubrey-Löchern (in der Abbildung weiße Kreise). Diese können unter Verwendung von Quadranten, die geographisch durch die vier Himmelsrichtungen in jeweils 14 Mondstationen geteilt sind, dazu verwendet worden sein, die ekliptikale Länge des Mondes in Bezug zum Frühlingspunkt oder zum Herbstpunkt beziehungsweise in Bezug zur Jupiterposition täglich zu markieren (der Mond erreicht den Jupiter ungefähr alle 27,5 Tage). In dieser Zählung wären alle 28 Mondhäuser halbiert, in eine Tagesstation und eine Nachtstation.

Zwischen dem dritten und vierten Mondhaus liegt das Goldene Tor der Ekliptik, wo der Frühlingspunkt zu Beginn der maltesischen Tarxien-Phase lag. Man beachte die fehlenden helleren ekliptiknahen Sterne im Trichter der Thuraya westlich davon, also rechts der Plejaden (ekliptikale Länge ungefähr 32 Bogengrad) bis hin zum Stern Hydor heutigen Sternbild Wassermann (Aquarius, ekliptikale Länge ungefähr 314 Bogengrad). Die hellsten ekliptiknahen Sterne in diesem Gebiet des Sternenhimmels Alpherg im Sternbild Fische (Pisces) sowie Hydor und Ancha im Sternbild Wassermann (Aquarius) erreichen lediglich die vierte Größenklasse (4^m), so dass zwischen dem auffälligen offenen Sternhaufen der Plejaden und Deneb Algedi, dem hellsten Stern im Sternbild Steinbock (Capricornus), auf einer Länge von 90 Bogengrad keine hellen ekliptiknahen Sterne vorhanden sind.

→ Zur Einteilung der Ekliptik nach den monatlichen Mondstationen siehe auch Exkurs Mondhäuser

→ Zum dunklen Himmelsquadranten entlang der Ekliptik siehe auch Exkurs Der Trichter der Thuraya

Drakonitischer Monat

Schematische Darstellung der Mondbahn (gelb) im Laufe eines drakonitischen Monats in Bezug auf die Ekliptiklinie (rot). Nach dem Erreichen der südlichsten Lage in Bezug zur Ekliptiklinie wird die Mondbahn aufsteigend, und von der nördlichsten Lage in Bezug auf die Ekliptiklinie wird die Mondbahn dann wieder absteigend. In der deutschsprachigen Schweiz gibt es für diese im Laufe eines drakonitischen Monats täglich mehr oder weniger deutlich wahrnehmbaren Änderungen der ekliptikalen Breite sogar eigene Adjektive. Das Ansteigen der ekliptikalen Breite des Mondes nach Norden wird obsigend und das Abfallen des Mondes nach Süden nidsigend genannt. Direkt auf der Ekliptik befinden sich der aufsteigende und der absteigende Knoten der Mondbahn.

Der drakonitische Monat ist durch den Verlauf der ekliptikalen Breite des Mondes in Bezug zur Ekliptiklinie beschrieben.

Deswegen gibt es noch den drakonitischen Monat (altgriechisch δράκων (drakon) beziehungsweise lateinisch draco = Drache), der eine Dauer von 27,212 Tagen hat. Diese Dauer beschreibt die Zeitpunkte, an denen die um gut 5 Bogengrad zur Ekliptik geneigte Mondbahn die Ekliptik kreuzt; die ekliptikale Breite des Mondes ist dann exakt null. Diese Schnittpunkte werden Mondknoten genannt und werden einmal im Monat im aufsteigenden Mondknoten und einmal im absteigenden Mondknoten erreicht. Befindet sich der Mond auf der Ekliptik, also in der Nähe dieser Mondknoten, kommt es bei dessen Sonnennähe (wenn der Neumond also in Konjunktion mit der Sonne steht) zu einer Sonnenfinsternis und bei dessen Sonnenferne (wenn der Vollmond also in Opposition zur Sonne steht) zu einer Mondfinsternis. Diese Mondpunkte wurden früher als Drachenpunkte bezeichnet, was sich aus der Vorstellung ableitete, dass ein Drache bei einer Mondfinsternis den Mond beziehungsweise bei einer Sonnenfinsternis die Sonne verschlingen würde.

Mit dem folgenden Java-Programm können die ekliptikalen Koordinaten der Sonne und des Mondes für jeden beliebigen Zeitpunkt eines Julianischen Datums in Julianischen Jahrhunderten in Bezug auf die astronomische Standardepoche J2000 berechnet werden:

→ Java-Programm "EkliptikaleKoordinatenMondSonne"

Die ekliptikalen Breiten des Mondes im Verlauf eines drakonitischen Monats beziehungsweise eines nur gut zweieinhalb Stunden längeren siderischen Monats mit gut 27 Tagen.

Die täglichen Änderungen der ekliptikalen Breite des Mondes in Bogengrad innerhalb eines Mondviertels

Tage nach aufsteigendem Knoten	Änderung der ekliptikalen Breite zum Vortag
1	1,2°
2	1,1°
3	1,0°
4	0,9°
5	0,6°
6	0,3°
7	0,0°

Simulation des Himmelsausschnitts beim Stern Regulus kurz vor der Bedeckung des Planeten Mars durch den Mond am 4. Mai 357 vor Christus von Athen aus gesehen.

Der Mond kann auf seiner Bahn im Laufe der Zeiten alle ekliptiknahen Himmelsobjekte inklusive aller Planeten und der Sonne bedecken und innerhalb einer Stunde wieder freigeben, die sich in einem Band bis zu gut ±5 Bogengrad nördlich oder südlich neben der Ekliptiklinie befinden.  Aristoteles (384 bis 322) hat dies in seiner Schrift "Über den Himmel" (altgriechisch: Περὶ οὐρανοῦ / Peri uranu) anhand der von ihm beobachteten Bedeckung des Planeten Mars durch den zunehmenden Halbmond in der Nähe des Sterns Regulus (α Leonis) beschrieben und darauf hingewiesen, dass die Babylonier und die Ägypter solche Phänomene über lange Zeit beobachtet und dokumentiert hatten.

Solche Ereignisse fanden zu Lebzeiten von Aristoteles von Griechenland aus gesehen nicht häufig statt:

• Am 6. April 357 vor Christus passierte der zunehmende Halbmond im Sternbild Löwe (Leo) nahe dem Stern Regulus (α Leonis) den Planeten Mars noch im Abstand von etwa einem Mondradius. Dieses Ereignis fand allerdings am Vormittag beim Aufgang der beiden Himmelskörper am östlichen Horizont statt, so dass dies von Griechenland aus nicht zu sehen war.
• Einen Monat später, am 4. Mai 357 vor Christus, bedeckte der zunehmende Halbmond den Planeten Mars abends gut sichtbar fast 60 Bogengrad über dem westsüdwestlichen Horizont sowie 4,5 Bogengrad östlich von Regulus über eine Stunde lang. Dies dürfte das Ereignis gewesen sein, über das der 27-jährige Aristoteles berichtet hat und das er in Athen selbst gesehen haben könnte.
• In den frühen Morgenstunden des 10. Mais 344 vor Christus bedeckte der zunehmende Mond im Sternbild Krebs (Cancer) westlich vom Stern Regulus (α Leonis) den Planeten Mars von seiner Schattenseite her gut eine halbe Stunde lang. Die beiden Sternbilder standen zu dieser Nachtzeit von Griechenland aus gesehen allerdings unterhalb des Horizonts.
• Am späten Abend des 31. Dezembers 343 verdeckte der Vollmond den Mars hoch am Himmel zwischen den Sternbildern Löwe und Krebs, was jedoch nicht zu der Beschreibung des zunehmenden Halbmonds von Aristoteles passt.
• Am Nachmittag des 4. März 340 verdeckte der fast volle Mond den Mars am Tageshimmel, was nicht beobachtet werden konnte.
• Die Bedeckung am 31. Mai 327 vor Christus fand ebenfalls nicht beobachtbar am Nachmittag statt.
• In der Morgendämmerung des 6. Septembers 326 vor Christus fand hoch am Himmel eine Bedeckung durch den abnehmenden Mond statt.
• Zwei Stunden nach Mitternacht am 27. Dezember 326 vor Christus fand hoch am Himmel eine Bedeckung durch den abnehmenden Mond statt.
• Die Bedeckung am 16. März 325 vor Christus durch den zunehmenden Mond war nur streifend und fand am Terminator des Mondes statt.

Der ekliptiknahe Hauptstern Pollux im Sternbild Zwillinge (Gemini) hat sich aufgrund seiner Eigenbewegung im Laufe der letzten zehntausend Jahre so weit von der Ekliptiklinie entfernt, dass er inzwischen nicht mehr vom Mond bedeckt werden kann.

→ Für die sieben hellsten Objekte siehe Exkurs Die sieben hellsten Objekte der Ekliptik.

Siderische Mondperioden

Der Mond erscheint innerhalb eines tropischen Jahres dreizehn- oder vierzehnmal an einer bestimmten Stelle des Fixsternhimmels, wobei er wegen der unterschiedlichen Periodendauern von siderischen und synodischen Monaten immer ein anderes Mondalter (die Anzahl der Tage seit dem letzten Neumond) und wegen der unterschiedlichen Periodendauern von siderischen und drakonitischen Monaten immer eine andere ekliptikale Breite aufweist.

Die beiden folgenden Diagramme sollen den zeitlichen Verlauf der Mondphasen und der ekliptikalen Breiten des Mondes bei seinem Erscheinen im Goldenen Tor der Ekliptik während 254 aufeinanderfolgender siderischer Perioden mit jeweils 27,322 Tagen (insgesamt 6940 Tage beziehungsweise 19 Jahre) veranschaulichen:

Die Mondphasen bei aufeinanderfolgenden Erscheinungen des Mondes im Goldenen Tor der Ekliptik innerhalb von 254 siderischen Perioden (insgesamt 19 Jahre). Da der synodische Monat (von Neumond zu Neumond) über zwei Tage länger ist als der siderische Monat, kommt es hierbei zu Verschiebungen, weil der Mond nach Ablauf eines siderischen Monats beim Erreichen derselben ekliptikalen Länge noch nicht ganz wieder sein maximales Mondalter erreicht hat.

In der oberen Hälfte des Diagramms sind zunehmende und in der unteren Hälfte abnehmende Monde zu beobachten. Eine Mondphase von 0 Prozent steht für einen Neumond und eine Mondphase von ±100 Prozent für einen Vollmond.

Der Startpunkt (Tag 0 im Monat 0) kann zum Beispiel mit dem 22. Mai 2020 am Abend (UTC) angesetzt werden, an dem der Neumond zusammen mit der Sonne im Goldenen Tor der Ekliptik stand. Dies geschieht dann nach 19 Jahren am 23. Mai 2039 kurz nach Mitternacht (UTC) erneut.

Die ekliptikalen Breiten des Mondes bei aufeinanderfolgenden Erscheinungen des Mondes im Goldenen Tor der Ekliptik innerhalb von 254 aufeinanderfolgenden siderischen Perioden (insgesamt 19 Jahre). Da der drakonitische Monat (von einem aufsteigendem Mondknoten bis zum nächsten aufsteigenden Mondknoten) gut zweieinhalb Stunden kürzer ist als der siderische Monat, kommt es hierbei zu Verschiebungen, weil der Mond nach Ablauf eines siderischen Monats den aufsteigenden Knoten bereits wieder hinter sich gelassen hat.

Bei großen ekliptikalen Breiten (oben) kommt es im Goldenen Tor der Ekliptik zu Bedeckungen der Plejaden und bei kleinen ekliptikalen Breiten (unten) kommt es zu Bedeckungen der Hyaden oder des Sterns Aldebaran durch die Mondscheibe.

Der Startpunkt (Tag 0 im Monat 0) kann beispielsweise ebenfalls mit dem 22. Mai 2020 angesetzt werden, an dem der Neumond vom Erdmittelpunkt aus gesehen bei einer ekliptikalen Breite von zirka -2,5 Bogengrad unterhalb der Sonne, deren ekliptikale Breite definitionsgemäß 0 Bogengrad beträgt, im Goldenen Tor der Ekliptik stand.

Nach 18,61 Jahren (beziehungsweise 6793,5 Tagen oder gut 230 synodischen Monaten, in dieser Abbildung also nach gut 248,6 siderischen Monaten) erreicht der Mond dieselbe ekliptikale Breite und fast die gleiche Mondphase, befindet sich dann allerdings bei einer anderen ekliptikalen Länge.

Die kurzperiodische kleine Wellenbewegung kommt durch die Nutation der Erdachse im Bezug zur Ekliptik beziehungsweise zum Fixsternhimmel zustande; sie hat eine Periodendauer von 35 Tagen und überlagert sich mit den zirka eine Woche kürzeren siderischen Mondperiode.

Der Meton-Zyklus

Nicht nur die Bestimmung und Vorhersage der Auf- und Untergänge der Venus haben die Aufmerksamkeit der Astronomen des Altertums auf sich gezogen, sondern auch der Mondzyklus mit den verschiedenen Mondphasen sowie das Auftreten von Mondfinsternissen bei Vollmond und von Sonnenfinsternissen bei Neumond. Es gibt einen Zyklus, der die Zeit beschreibt, nachdem die Sonne und der Mond die gleiche Konstellation erreichen. Nach 19 Jahren (beziehungsweise knapp 6940 Tagen) hat nicht nur die Sonne dieselbe ekliptikale Länge erreicht, sondern auch der der Mond (nach 254 siderischen Monaten), und er hat daher auch dieselbe Mondphase (nach 235 synodischen Monaten). Außerdem hat er dann auch noch annährend die gleiche ekliptikale Breite (nach 255 drakonitischen Monaten), so dass er fast wieder an derselben Stelle des Fixsternhimmels steht.

Der Zyklus beruht also im Wesentlichen auf der zwar nur langfristig, bei entsprechender Ausdauer jedoch verhältnismäßig einfach zu beobachtenden Tatsache, dass 19 tropische Sonnenjahre, 235 synodische Monate, 254 siderische Monate und 255 drakonitische Monate fast die gleiche Länge haben. Der Unterschied zwischen den ersten beiden beträgt nur rund zwei Stunden:

• 19 Jahre = 6939,6 Tage, bestimmt durch die ekliptikale Länge der Sonne mit ihren Äquinoktien und Sonnenwenden.
• 235 synodische Monate = 6939,7 Tage, bestimmt durch die Mondphasen mit Neumonden und Vollmonden.
• 254 siderische Monate = 6939,7 Tage, bestimmt durch die ekliptikale Länge des Mondes.
• 255 drakonitische Monate = 6939,1 Tage, bestimmt durch die auf- und absteigenden Knoten der Mondbahn.

Legende zum Diagramm "Meton-Zyklus".

• Der Meton-Zyklus
• 
  Der Meton-Zyklus anhand der Frühlingsvollmonde (weiße Kreise) am 21. März 2019 (laufende Nummer 0) und am 21. März 2038 (laufende Nummer 235).
• 
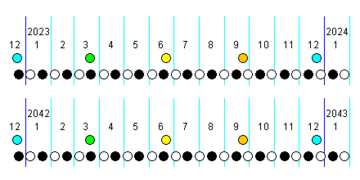
  Der Meton-Zyklus vom Vollmond am 6. Januar 2023 bis zum Vollmond am 6. Januar 2042. Die farbigen Kreise symbolisieren die Äquinoktien und Sonnenwenden.

Der 19-jährige Meton-Zyklus vom Januar 2023 bis zum Januar 2042. Die Zeit schreitet in horizontaler Richtung jeweils um einen halben Tag pro Bildpunkt voran. Der Vollmond (weißer Kreis) erscheint sowohl am 6. Januar 2023 als auch am 6. Januar 2042 im Sternbild Zwillinge (Gemini) nördlich vom Stern Mebsuta (ε Geminorum). Unten sind die kleinen und großen Mondwenden für die geographische Breite 52,5 Bogengrad (zum Beispiel in Berlin) im Laufe der Zeit dargestellt.

Dieser 19-jährige nach dem antiken griechischen Astronomen  Meton (5. Jahrhundert vor Christus) benannte Meton-Zyklus sowie auch der unten erwähnte Saros-Zyklus waren im Altertum spätestens schon den Babyloniern bekannt und dienten als Grundlage für ihren Mondkalender. Meton ist davon ausgegangen, dass 19 Jahre exakt mit 6940 Tagen sowie mit 235 synodischen Monaten übereinstimmen. Dadurch, dass das Jahr nach dieser Annahme genau fünf Neunzehntel Tage länger ist als 365 Tage, sind neunzehn Jahre nach dieser Berechnung genau fünf Tage länger ist als neunzehn Mal 365 Tage, also 6935 Tage. Aus der Annahme einer festen ganzrationalen Kopplung der Umlaufzeiten der Erde um Ihre Achse (Tag) und um die Sonne (Jahr) sowie der Umlaufzeit des Mondes um die Erde (Monat) ergeben sich die folgenden Zusammenhänge:

• Abgerundet auf ganze Zahlen:
  • Die Jahreslänge in ganzen Tagen:

    ${\frac {6940}{19}}=365{\text{ Rest }}5$, das heißt, dass für 19 Jahre mit der Länge 365 Tage fünf Schalttage (Jahreslänge dann 366 Tage) erforderlich sind, damit der Frühlingspunkt mit dem tropischen Sonnenjahr synchron bleibt (Solarkalender).

  • Die Monatslänge in ganzen Tagen:

    ${\frac {6940}{235}}=29{\text{ Rest }}125$, das heißt, dass für 235 synodische Monate mit der Länge 29 Tage 125 Schalttage (Monatslänge dann 30 Tage) erforderlich sind, damit ein tropisches Sonnenjahr immer zwölf Monate umfasst (Solarkalender).

  • Die Jahreslänge in ganzen Monaten:

    ${\frac {\frac {6940}{19}}{\frac {6940}{235}}}={\frac {235}{19}}=12{\text{ Rest }}7$, das heißt, dass in 19 Jahren mit 235 synodischen Monaten sowie 6490 Tagen sieben synodische Schaltmonate (Jahreslänge dann 13 Monate) erforderlich sind, um das Kalenderjahr mit dem tropischen Sonnenjahr synchron zu halten (Lunisolarkalender).

• Exakt mit Brüchen (ganzrationale Zahlen):
  • Die Jahreslänge $d_{a}$ in Tagen (in einem Sonnenjahr):

    $d_{a}={\frac {6940{\text{ d}}}{19{\text{ a}}}}=365{\frac {\text{d}}{\text{a}}}+{\frac {5}{19}}{\frac {\text{d}}{\text{a}}}=365{\frac {\text{d}}{\text{a}}}+{\frac {20}{76}}{\frac {\text{d}}{\text{a}}}=365{\frac {\text{d}}{\text{a}}}+{\frac {1}{4}}{\frac {\text{d}}{\text{a}}}+{\frac {1}{76}}{\frac {\text{d}}{\text{a}}}=365,25{\frac {\text{d}}{\text{a}}}+{\frac {1}{76}}{\frac {\text{d}}{\text{a}}}\approx 365,263158{\frac {\text{d}}{\text{a}}}$

  • Die Länge eines synodischen Monats $d_{m}$ in Tagen:

    $d_{m}={\frac {6940{\text{ d}}}{235{\text{ m}}}}={\frac {1388}{47}}{\frac {\text{d}}{\text{m}}}=29{\frac {\text{d}}{\text{m}}}+{\frac {125}{235}}{\frac {\text{h}}{\text{m}}}=29{\frac {\text{d}}{\text{m}}}+{\frac {25}{47}}{\frac {\text{h}}{\text{m}}}\approx 29,531915{\frac {\text{d}}{\text{m}}}$

  • Länge von zwölf synodischen Monaten $d_{m_{12}}$ in Tagen (in einem Mondjahr):

    $d_{m_{12}}=12{\frac {\text{m}}{\text{a}}}\cdot d_{m}=12{\frac {\text{m}}{\text{a}}}\cdot {\frac {1388}{47}}{\frac {\text{d}}{\text{m}}}={\frac {16656}{47}}{\frac {\text{d}}{\text{a}}}\approx 354,382979{\frac {\text{d}}{\text{a}}}\approx d_{a}-11{\frac {\text{d}}{\text{a}}}$

  • Die Jahreslänge $m_{a}$ in synodischen Monaten (in einem Sonnenjahr):

    $m_{a}={\frac {d_{a}}{d_{m}}}={\frac {\frac {6940{\text{ d}}}{19{\text{ a}}}}{\frac {6940{\text{ d}}}{235{\text{ m}}}}}={\frac {235}{19}}{\frac {\text{m}}{\text{a}}}=12{\frac {\text{m}}{\text{a}}}+{\frac {7}{19}}{\frac {\text{m}}{\text{a}}}\approx 12,368421{\frac {\text{m}}{\text{a}}}$

Anmerkung: Man nehme zur Kenntnis, dass das der Mittelwert der Dauern vom Sonnenjahr $d_{a}$ und vom Mondjahr $d_{m_{12}}$ fast genau 360 Tage pro Jahr beträgt, also so viele Tage wie für einen vollständigen Kreis in Bogengrad gerechnet wird:

${\frac {d_{a}+d_{m_{12}}}{2}}={\frac {{\frac {6940{\text{ d}}}{19{\text{ a}}}}+{\frac {16656}{47}}{\frac {\text{d}}{\text{a}}}}{2}}={\frac {321322}{893}}{\frac {\text{d}}{\text{a}}}\approx 359,823{\frac {\text{d}}{\text{a}}}\approx 360{\frac {\text{d}}{\text{a}}}$

Mit den heutigen, jeweils rund eine halbe Stunde kürzeren Messwerten für die beiden Jahresdauern (tropisches Sonnenjahr mit 365,241 Tagen und Mondjahr mit zwölf Lunationen und 354,367 Tagen) zur Epoche J2000.0 ergibt sich ein nur geringfügig anderer Mittelwert, der ebenfalls nur um zirka eine Dreiviertelstunde von der Dauer von 360 Tagen abweicht:

${\frac {d_{a}+d_{m_{12}}}{2}}={\frac {365,241{\frac {\text{d}}{\text{a}}}+354,367{\frac {\text{d}}{\text{a}}}}{2}}\approx 359,804{\frac {\text{d}}{\text{a}}}\approx 360{\frac {\text{d}}{\text{a}}}$

Für diese Erkenntnisse ist entweder die Weitergabe von beobachteten astronomischen Ereignissen, wie der Bedeckung der Plejaden durch den Mond oder die Messung der ekliptikalen Koordinaten des Mondes, an die nächste Generation erforderlich oder ein Lebensalter, das die Beobachtung von mindestens zwei solcher Zyklen umfasst – je nach Zeitpunkt der Geburt also rund 25 bis über 40 Jahre.

Da der Meton-Zyklus mit den aufgerundeten ganzzahligen 6940 Tagen einen Vierteltag länger dauert als 19 Sonnenjahre, summiert sich diese Differenz nach vier Meton-Zyklen auf einen ganzen Tag. Der entsprechende nach  Kallippos von Kyzikos (viertes vorchristliches Jahrhundert) benannte Kallippische Zyklus von 76 Jahren ($=4\cdot 19$ Jahre) oder 27759 Tage ($=(4\cdot 6940)-1$ Tage) wird auch als verbesserter Meton-Zyklus bezeichnet:

• 76 Jahre = 27758,4 Tage
• 940 synodische Monate = 27758,8 Tage
• 1016 siderische Monate = 27758,8 Tage
• 1020 drakonitische Monate = 27756,5 Tage

Nach ungefähr 48 Sonnenjahren betrug die Differenz zwischen Meton-Zyklus und Sonnenjahr einen Tag, aber erst nach ungefähr 128 Sonnenjahren erreicht die Differenz zwischen Kallippischen Zyklus und Sonnenjahr so groß. Da der Kallippische Zyklus mit genau 27759;Tagen einen Vierteltag länger dauert als 76 Sonnenjahre, summiert sich diese Differenz nach vier Kallippischen Zyklen auf einen ganzen Tag. Der entsprechende nach  Hipparchos von Nicäa (zweites vorchristliches Jahrhundert) benannte Hipparchos-Zyklus von 304 Jahren ($=4\cdot 76=16\cdot 19$ Jahre) = 111035 Tage ($=(4\cdot 27759)-1$ Tage) ist also wiederum ein verbesserter Kallippischer Zyklus:

• 304 Jahre = 111033,6 Tage
• 3760 synodische Monate = 111035,0 Tage
• 4064 siderische Monate = 111035,2 Tage
• 4080 drakonitische Monate = 111025,9 Tage

Nach einer Kallippischen Periode beträgt die Differenz zwischen 111035 ganzen Tagen und der Dauer von 3760 synodischen Monaten nur eine dreiviertel Stunde.

Die folgende Tabelle gibt einen Überblick über die Dauern im Meton-Zyklus, im Kallippischen Zyklus und im Hipparchos-Zyklus:

	Tropische Perioden	Synodische Perioden	Siderische Perioden	Ganzzahlige Tage
Dauer einer Periode in Tagen	365,2422	29,53059	27,32166	1
Anzahl der Perioden im Meton-Zyklus	19	235	254	6940
Anzahl der Tage im Meton-Zyklus	6939,6018	6939,6887	6939,7016	6940
Differenz zu tropischen Perioden in Tagen	0,0000	0,0868	0,0998	0,3982
Differenz zu synodischen Perioden in Tagen	-0,0868	0,0000	0,0130	0,3113
Differenz zu siderischen Perioden in Tagen	-0,0998	-0,0130	0,0000	0,2984
Differenz zu tropischen Perioden in Stunden	0,00	2,08	2,40	9,56
Differenz zu synodischen Perioden in Stunden	-2,08	0,00	0,31	7,47
Differenz zu siderischen Perioden in Stunden	-2,40	-0,31	0,00	7,16
Anzahl der Perioden im Kallippischen Zyklus	76	940	1016	27759
Anzahl der Tage im Kallippischen Zyklus	27758,4072	27758,7546	27758,8066	27759
Differenz zu tropischen Perioden in Tagen	0,0000	0,3474	0,3994	0,5928
Differenz zu synodischen Perioden in Tagen	-0,3474	0,0000	0,0520	0,2454
Differenz zu siderischen Perioden in Tagen	-0,3994	-0,0520	0,0000	0,1934
Differenz zu tropischen Perioden in Stunden	0,00	8,34	9,58	14,23
Differenz zu synodischen Perioden in Stunden	-8,34	0,00	1,25	5,89
Differenz zu siderischen Perioden in Stunden	-9,58	-1,25	0,00	4,64
Anzahl der Perioden im Hipparchos-Zyklus	304	3760	4064	111035
Anzahl der Tage im Hipparchos-Zyklus	111033,6288	111035,0184	111035,2262	111035
Differenz zu tropischen Perioden in Tagen	0,0000	1,3896	1,5974	1,3712
Differenz zu synodischen Perioden in Tagen	-1,3896	0,0000	0,2078	-0,0184
Differenz zu siderischen Perioden in Tagen	-1,5974	-0,2078	0,0000	-0,2262
Differenz zu tropischen Perioden in Stunden	0,00	33,35	38,34	32,91
Differenz zu synodischen Perioden in Stunden	-33,35	0,00	4,99	-0,44
Differenz zu siderischen Perioden in Stunden	-38,34	-4,99	0,00	-5,43

Vor gut 2000 Jahren betrug die Differenz zwischen Kallippischem Zyklus und Sonnenjahr nach ungefähr 227 Sonnenjahren einen Tag. Durch die inzwischen etwas verkürzte Dauer eines tropischen Jahres ist dies heute bereits nach etwa 221 Jahren der Fall.

Die Goldene Zahl gibt an, das wievielte von diesen 19 Jahren ein bestimmtes Jahr ist, und sie spielt auch heute noch eine wichtige Rolle bei der Bestimmung des Datums von Pessach oder Ostern, zum Beispiel mit Hilfe der Formeln zur Berechnung von  Carl Friedrich Gauß (* 1777; † 1855):

• → siehe auch Wikibook Osterdatum
•  Gaußsche Pessach-Formel
•  Gaußsche Osterformel

Der Name Goldene Zahl rührt möglicherweise davon her, dass der diesem Zyklus zugrundeliegende Kalender (Parapegma) des Meton auf den Steinmauern seiner Sonnenuhr (heliotropion) am Pnyx-Hügel in Athen in goldener Schrift zu sehen war.

Heute ist in den Monaten um die Wintersonnenwende alle 19 Jahre morgens am westlichen Horizont der untergehende Vollmond im Goldenen Tor der Ekliptik zu sehen, wie zuletzt im Dezember 2018. Die untere Hälfte des Mondes wird dann während des Untergangs vom Horizont verdeckt und der sichtbare leuchtende Teil bildet somit einen Halbkreis, wie er im mittleren Segment der Himmelstafel angedeutet ist. In diesem Fall liegen Hyaden und Plejaden im Westen auf einer Linie parallel zum Horizont und der dazwischenliegende, beim Untergang noch halb zu sehende Vollmond würde der Abbildung auf der Steintafel von Tal-Qadi entsprechen. Vor 4500 Jahren ergab sich diese Himmelsansicht wegen der Verschiebung des Frühlingspunktes bereits um die Tag-und-Nacht-Gleiche im Herbst.

Die 19 Megalithe des Blaustein-Hufeisens von Stonehenge (2270 bis 1930 vor Christus) werden ebenfalls mit dem Meton-Zyklus in Zusammenhang gesehen. Im Übrigen werden beispielsweise auch die Goldhüte aus der Bronzezeit mit diesem Zyklus in Verbindung gebracht.

Detail mit den linken drei der insgesamt neunzehn Göttinnen der Bilderreihe in der Kammer A des hethitischen Heiligtums Yazılıkaya.

An der östlichen Wand in der Kamme A des hethitischen Heiligtums Yazılıkaya (türkisch für „beschriebener Fels“) aus dem 13. vorchristlichen Jahrhundert existiert eine Reliefbilderreihe, die eine Prozession von neunzehn nach links schauenden Göttinnen im Ganzkörperprofil darstellt. Auch hier wird vermutet, dass diese Reihe als Zählwerk für den Meton-Zyklus eine Kalenderfunktion innehatte.

Schmatische Darstellung der neunzehn weiblichen Gottheiten im hethitischen Heiligtum Yazılıkaya. Im Original variieren die Darstellungen der einzelnen Figuren, die in unterschiedlichem Zustand erhalten sind. Über den Händen einzelner Figuren konnten verschiedene hieroglyphische Darstellungen festgestellt werden. Die erste Figur (ganz links) konnte hierdurch nur indirekt rekonstruiert werden.

Die auf den MUL.APIN-Tafeln schriftlich überlieferten babylonischen Plejaden-Schaltregeln beziehen sich zweifelsfrei auf einen Zeitpunkt, als der offene Sternhaufen der Plejaden im Sternbild Stier (Taurus) die gleiche ekliptikale Länge wie der Frühlingspunkt gehabt hat. Dies bedeutet, dass die Sonne zur Tag-und-Nacht-Gleiche direkt neben den Plejaden stand, und dies war um 2600 vor Christus der Fall. Aus beiden Schaltregeln ergibt sich, dass innerhalb von 19 Sonnenjahren sieben zusätzliche synodische Monate eingeschaltet werden müssen, damit Sonnen- und synodisches Mondjahr synchron bleiben. Die Differenz zwischen Mondlauf und Sonnenlauf beträgt nach diesen 19 Sonnenjahren nur gut zwei Stunden. Diese Abweichung beträgt nur gut zwei Promille beziehungsweise 238 parts per million:

• Tropisches Sonnenjahr (von Frühlingspunkt zu Frühlingspunkt): $J_{S}=365,2422{\text{ d}}=8765,813{\text{ h}}$
• Synodischer Monat (von Neumond zu Neumond): $M_{syn}=29,53059{\text{ d}}=708,7342{\text{ h}}$
• Synodisches Mondjahr (zwölf synodische Monate): $J_{syn}=12\cdot M_{syn}=354,3671{\text{ d}}=8504,810{\text{ h}}$
• Jahresdifferenz zwischen tropischem Sonnenjahr und synodischem Mondjahr: $\Delta J=J_{S}-J_{syn}=10,8751{\text{ d}}=261,003{\text{ h}}$
• Meton-Zyklus: $19\cdot \Delta J=206,627{\text{ d}}=4959,046{\text{ h}}$ beziehungsweise $7\cdot M_{syn}=206,714{\text{ d}}=4961,139{\text{ h}}$
• Genauigkeit des Meton-Zyklus: $\Delta M=7\cdot M_{syn}-19\cdot \Delta J=0,087{\text{ d}}\approx 2,09{\text{ h}}=235\cdot M_{syn}-19\cdot J_{S}$
• Arithmetische Zusammensetzung und Primfaktorenzerlegung der Anzahl synodischer Mondzyklen: $235=7+19\cdot 12=5\cdot 47$

Mit anderen Worten war der Meton-Zyklus bereits über zwei Jahrtausende lang bekannt, bevor sich der griechische Astronom Meton damit beschäftigte.

Es ist äußerst bemerkenswert, dass eine entsprechende Berechnung auch für dreizehn siderische Monate durchgeführt werden kann, bei denen der Mond jeweils einmal vollständig die Ekliptik mit ihren zwölf Ekliptiksternbildern beziehungsweise den 27 oder 28 Mondstationen (auch Mondhäuser genannt, siehe auch Exkurs Mondhäuser) durchläuft:

• Tropisches Sonnenjahr (von Frühlingspunkt zu Frühlingspunkt): $J_{S}=365,2422{\text{ d}}=8765,813{\text{ h}}$
• Siderischer Monat (von Fixstern zu Fixstern): $M_{sid}=27,32166{\text{ d}}=655,720{\text{ h}}$
• Siderisches Mondjahr (13 siderische Monate): $J_{sid}=13\cdot M_{sid}=355,1816{\text{ d}}=8524,358{\text{ h}}$
• Jahresdifferenz zwischen tropischem Sonnenjahr und siderischem Mondjahr: $\Delta J=J_{S}-J_{sid}=10,0606{\text{ d}}=241,454{\text{ h}}$
• Meton-Zyklus: $19\cdot \Delta J=191,151{\text{ d}}=4587,634{\text{ h}}$ beziehungsweise $7\cdot M_{sid}=191,252{\text{ d}}=4590,040{\text{ h}}$
• Genauigkeit des Meton-Zyklus: $\Delta M=7\cdot M_{sid}-19\cdot \Delta J=0,100{\text{ d}}\approx 2,40{\text{ h}}=254\cdot M_{sid}-19\cdot J_{S}$
• Arithmetische Zusammensetzung und Primfaktorenzerlegung der Anzahl siderischer Mondzyklen: $254=7+19\cdot 13=2\cdot 127$

Auch hier beträgt die Differenz zwischen Mondlauf und Sonnenlauf nur gut zwei Stunden. Und innerhalb der 19 Sonnenjahre eines Meton-Zyklus müssen auch hier sieben zusätzliche (vierzehnte) siderische Monate eingeschaltet werden, damit Sonnen- und siderisches Mondjahr synchron bleiben.

Zur Differenz von knapp elf Tagen zwischen Sonnen- und Mondjahr siehe auch das babylonische Neujahrsfest Akiti. Dieses elftägige Fest wurde am Ende des Mondjahres gefeiert.

Der drakonitische Zyklus

Ferner existiert ein zirka 18,61-jähriger Mondzyklus, der darauf beruht, dass bedingt durch die Präzession der Mondbahn der aufsteigende und der absteigende Mondknoten nach dieser Zeit die Ekliptik entgegen der rechtläufigen (prograden) Umlaufrichtung des Mondes genau einmal vollständig rückläufig (retrograd) durchlaufen haben. Dieser Zyklus besteht aus 249,83 drakonitischen Monaten, die insgesamt 6798,38 Tagen beziehungsweise 18,61 tropischen Sonnenjahren entsprechen. Die ekliptikalen Längen der Mondknoten vermindern sich hierbei um einen Winkel von 19,34 Bogengrad pro Jahr.

Dieser drakonitische Zyklus ist zum Beispiel anhand der Abweichungen der ekliptikalen Breiten des Mondes und somit der Azimute bei den monatlichen Mondauf- und -untergängen am Horizont zu beobachten, die sich nach 18,61 Jahren wiederholen und dabei um die Punkte der Wintersonnenwende im Südosten und Südwesten sowie die Punkte der Sommersonnenwende im Nordosten und Nordwesten entlang dem Horizont pendeln. Die Zeitpunkte an dem die entsprechenden Auf- und Untergangspunkte zwischen dem nördlichen und dem südlichen Horizont um die Punkte der Tag-und-Nacht-Gleichen im Osten und Westen, die definitionsgemäß bei der ekliptikalen Breite null genau in der Ekliptik liegen, am engsten beziehungsweise am weitesten auseinanderliegen, heißen große und kleine Mondwenden. Diese Mondwenden wiederholen sich also alle 18,61 Jahre. Hierbei treten auch extrem große und extrem kleinen Mondwenden auf. Um die Wintersonnenwenden der Jahre 2023, 2042, 2061 und so weiter treten beispielsweise größte Mondwenden auf, bei denen die Auf- und Untergangspunkte weit in Richtung Norden von den genau im Osten und im Westen liegenden Äquinoktialpunkten entfernt sind. Und um die Sommersonnenwenden der Jahre 2024, 2043, 2062 und so weiter treten kleinste Mondwenden auf, bei denen die Auf- und Untergangspunkte weit in Richtung Süden von den genau im Osten und im Westen liegenden Äquinoktialpunkten entfernt sind.

Die sieben hellsten feststehenden Himmelsobjekte in der Nähe der Ekliptik liegen zwischen den Sternbildern Stier (Taurus, rechts) und Skorpion (Scorpio, links). Der Bogen der Ekliptik wird von den Wandelgestirnen entgegen dem Uhrzeigersinn vom Frühlingspunkt rechts zum Herbstpunkt links durchlaufen. In der Nähe unteren Bogenhälfte befinden sich keine hellen Fixsterne in der Nähe der Ekliptik, der helle Stern Fomalhaut (α Piscis Austrini) im Sternbild Südlicher Fisch (Piscis Austrinus) dient lediglich zur Orientierung. Außerhalb des Bogens liegende Punkte befinden sich nördlich der Ekliptik und innen liegende südlich.

Aufgrund dieser Zusammenhänge werden alle möglichen Positionen des Mondes in Bezug auf die Ekliptik bei den ekliptikalen Längen von -180 bis +180 Bogengrad und den ekliptikalen Breiten von ungefähr -6 bis +6 Bogengrad innerhalb dieser 18,61-jährigen Periode erreicht. Somit erfolgen auch alle möglichen Sternbedeckungen (Okkultationen) oder nahe Konjunktionen innerhalb dieser Periodendauer und wiederholen sich danach im drakonitischen Zyklus. Die Bedeckungen hellsten ekliptiknahen Himmelsobjekte sind hierbei besonders spektakulär und gut zu beobachten. Dies gilt insbesondere für:

• die Plejaden (Messier 45, 1,5^m) im Sternbild Stier (Taurus)
• die Hyaden (0,5^m) im Sternbild Stier (Taurus)
• den Roten Riesen Aldebaran (α Tauri, 1,0^m) im Sternbild Stier (Taurus)
• den Roten Überriesen Antares (α Scorpii, 1,0^m) im Sternbild Skorpion (Scorpio),
• den Stern Spica (α Virginis, 1,0^m) im Sternbild Jungfrau (Virgo)
• den Stern Regulus (α Leonis, 1,5^m) im Sternbild Löwe (Leo)

Wenn der Mond bei der Bedeckung der Plejaden seine maximale nördliche ekliptikale Breite bereits zuvor erreicht hatte und sich also bereits wieder in Richtung seines absteigenden Knotens bewegt, befindet sich in der Nähe des absteigenden Knotens der Königsstern Regulus im Sternbild Löwe (Leo), so dass es ungefähr eine Woche später ebenfalls zu dessen Bedeckung durch den Mond kommen kann. Da der Stern Antares α Scorpii) im Sternbild Skorpion (Scorpio) in etwa die gleiche südliche ekliptikale Breite hat wie die Plejaden eine nördliche ekliptikale Breite haben und beide auf gegenüberliegenden Punkten der Ekliptiklinie liegen, kommt es im Rhythmus des drakonitischen Zyklus innerhalb eines halben Monats gehäuft zu der Bedeckung beider Himmelsobjekte durch die Mondscheibe. Beide Ereignisse wären wegen der gegenüberliegenden Lage auf der Ekliptik heute allerdings nur während der langen Nächte im Winterhalbjahr zu sehen, wenn Antares praktisch nicht zu beobachten ist, weil er von der Sonne überstrahlt wird. Als der Frühlingspunkt im Altertum jedoch im Sternbild Stier stand, war die aufeinanderfolgende Bedeckung von Plejaden und Antares jedoch durchaus ein zu beobachtendes Doppelereignis.

Das nächste Mal werden die beiden eng benachbarten Elternsterne der Plejaden (der Titan Atlas und die Okeanide Pleione) von Mitteleuropa aus gesehen in den Morgenstunden des 8. Augusts 2024 von der Scheibe des abnehmenden Halbmonds bedeckt. Am 1. April 2025 werden gegen Mitternacht dann sogar mehrere helle Sterne des Sternhaufen durch die nur vier Tage alte Mondsichel bedeckt.

Auch im alten chinesischen, mündlich überlieferten Volksmärchen „Morgenhimmel“ wird der Zyklus vom Stern des großen Jahres erwähnt, der sich erst nach 18 Jahren, also im 19. Jahr wiederholt:

Als Morgenhimmel gestorben war, berief der Kaiser den Sterndeuter und fragte: „Kanntest du Morgenhimmel?“
Der sagte: „Nein.“
Der Kaiser fragte: „Was verstehst du denn?“
Der Sterndeuter sagte: „Ich kann nach den Sternen sehen.“
„Sind alle Sterne an ihrem Platz?“ fragte der Kaiser.
„Ja. Nur den Stern des großen Jahres habe ich achtzehn Jahre nicht gesehen. Jetzt aber ist er wieder sichtbar.“
Da blickte der Kaiser zum Himmel auf und seufzte: „Achtzehn Jahre lang war Morgenhimmel mir zur Seite, und ich wusste nicht, dass er der Stern des großen Jahres war.“

Mit "Stern des großen Jahres" könnte ein Ereignis gemeint sein, bei dem der Mond alle 18,61 Jahre einen bestimmten hellen und ekliptiknahen Stern bedeckt, wie zum Beispiel einen der drei Königssterne Aldebaran (α Tauri) im Sternbild Stier (Taurus), Regulus (α Leonis) im Sternbild Löwe (Leo), Antares (α Scorpii) im Sternbild Skorpion (Scorpio) oder auch Spica (α Virginis) im Sternbild Jungfrau (Virgo).

Auch für den drakonitischen Zyklus kann für dreizehn drakonitische Monate eine Berechnung in Bezug auf den 19-jährigen Meton-Zyklus durchgeführt werden:

• Tropisches Sonnenjahr (von Frühlingspunkt zu Frühlingspunkt): $J_{S}=365,2422{\text{ d}}=8765,813{\text{ h}}$
• Drakonitischer Monat (von Mondknoten zu Mondknoten): $M_{dra}=27,21222{\text{ d}}=653,093{\text{ h}}$
• Drakonitisches Mondjahr (13 drakonitische Monate): $J_{dra}=13\cdot M_{dra}=353,7589{\text{ d}}=8490,213{\text{ h}}$
• Jahresdifferenz zwischen tropischem Sonnenjahr und drakonitischem Mondjahr: $\Delta J=J_{S}-J_{dra}=11,4833{\text{ d}}=275,600{\text{ h}}$
• Meton-Zyklus: $19\cdot \Delta J=218,1835{\text{ d}}=5236,403{\text{ h}}$ beziehungsweise $8\cdot M_{sid}=217,6978{\text{ d}}=5224,746{\text{ h}}$
• Genauigkeit des Meton-Zyklus: $\Delta M=8\cdot M_{dra}-19\cdot \Delta J=-0,486{\text{ d}}\approx -11,66{\text{ h}}=-(255\cdot M_{dra}-19\cdot J_{S})$
• Arithmetische Zusammensetzung und Primfaktorenzerlegung der Anzahl drakonitischer Mondzyklen: $255=8+19\cdot 13=3\cdot 5\cdot 17$

Hier beträgt die Differenz zwischen Mondlauf und Sonnenlauf knapp einen halben Tag. Innerhalb der 19 Sonnenjahre eines Meton-Zyklus müssen hier acht zusätzliche (vierzehnte) drakonitische Monate eingeschaltet werden, damit Sonnen- und drakonitisches Mondjahr synchron bleiben.

Der Saros-Zyklus

Der Saros-Zyklus umfasst sowohl eine Periode von 242 drakonitischen Monaten als auch eine Periode von 223 synodischen Monaten. Das sind gut 6585 Tage oder 18,03 tropische Sonnenjahre, also 18 Jahre und knapp 11 Tage). In der Graphik ist die Zeit vom aufsteigenden Knoten (rot) am 1. Januar 2023 bis zum aufsteigenden Knoten (rot) am 11. Januar 2041 dargestellt. Man beachte die gleichzeitige zyklische Wiederholung der jeweiligen Mondphasen sowie daraus folgend der Finsternisse im April und Mai sowie im Oktober und November mit einer Verschiebung von elf Kalendertagen im Sonnenjahr.
Die Mondwenden (die tagesaktuellen Auf- und Untergangsazimute des Mondes sind im unteren Bereich für die geographische Breite 52,5 Bogengrad (zum Beispiel in Berlin) dargestellt) haben ihr Minimum und Maximum demzufolge zu den entsprechenden Zeitpunkten, die Ausprägung dieser Extrema unterscheidet sich jedoch ein wenig, weil der Mond dort geringfügig abweichende minimale und maximale ekliptikale Breiten hat. Die kleinen Mondwenden beim Sommervollmond im Juli und die großen Mondwenden beim Wintervollmond (Jahreswechsel) sind in der Graphik ebenfalls nachvollziehbar.

Legende

Über die weiter oben beschriebenen Koinzidenzen hinaus kann beobachtet werden, dass der Mond nach 18,03 Jahren (also nach 242 drakonitischen Monaten beziehungsweise 6585,3 Tagen) denselben auf- oder absteigenden Knoten erreicht, wobei Sonne und Mond dann die gleiche Elongation haben (nach 223 synodischen Monaten beziehungsweise 6585,2 Tagen). Sie befinden sich dann allerdings nur fast bei den gleichen ekliptikalen Längen beziehungsweise an den gleichen Stellen des Fixsternhimmels, da diese Dauer nur mit ungefähr einem halben Tag Differenz mit 241 siderischen Perioden übereinstimmt (6584,6 Tage). Innerhalb dieses halben Tages hat sich die Sonne um zirka ein halbes Bogengrad und der Mond sogar um ungefähr sechseinhalb Bogengrad weiterbewegt.

Dieser Zyklus wird Saros-Zyklus genannt. Innerhalb dieser Zeitspanne ergibt sich eine Reihe von Sonnen- und Mondfinsternissen, die sich in ihrer Abfolge immer wieder ähneln. Der Saros-Zyklus war bei den Babyloniern bereits im Altertum bekannt, was in Keilschrift geschrieben auf Tontafeln aus der Mitte des achten vorchristlichen Jahrhunderts überliefert ist.

Heute werden die sich wiederholenden Sonnen- und Mondfinsternisse, die sich auf einen bestimmten auf- oder absteigenden Knoten der Mondbahn beziehen und jeweils eine Lebensdauer von mehreren Jahrhunderten haben, zum Zwecke der Unterscheidung mit Nummern versehen. Zu einem bestimmten Zeitpunkt der Weltgeschichte sind immer mehrere Dutzend Saros-Zyklen gleichzeitig aktiv.

Die anomalistische Periode steht für die Dauer, bis der Mond auf seiner elliptischen Bahn um die Erde erneut eines seiner beiden Apogäen erreicht, also das Perigäums (erdnächster Punkt) oder das Apogäum (erdfernster Punkt). Nach einer ganzzahligen vielfachen Dauer der anomalistischen Periode hat der Mond also stets fast die gleiche Entfernung zur Erde und somit auch die gleiche scheinbare Größe, so dass die Dauer und Art (totale oder ringförmige Sonnenfinsternis) einer Finsternis sich wiederholt.

Wegen der gleichen ekliptikalen Breiten des Mondes nach einer ganzzahligen vielfachen Dauer der drakonitischen Periode erscheint der Mondschatten auf der Erdoberfläche nach der Dauer einer Saros-Periode ungefähr beim gleichen Breitengrad. Durch die Differenz von rund einem drittel Tag ist der Längengrad allerdings nach einer Saros-Periode um knapp 120 Bogengrad nach Westen verschoben. Nach drei Saros Perioden, oder nach einem dadurch definierten Exeligmos-Zyklus, haben sich die drei Dritteltage fast auf einen Tag summiert, so dass nach der Mondschatten dann nicht nur wieder beim ähnlichen Breitengrad, sondern sogar beim ähnlichen Längengrad und zu einer ähnlichen Tageszeit auftaucht. Anders ausgedrückt: wenn an einem bestimmten Ort auf der Erdoberfläche eine Finsternis auftritt, so erfolgt in der Regel nach 19756 Tagen (54 Jahren und 33 Tagen) in dieser geographischen Region mit nur rund einer Stunde Verfrühung erneut eine solche Finsternis.

Exeligmos-Zyklus

Anzahl der Saros-Zyklen	Dauer in tropischen Jahren	Dauer in ganzen Tagen
1	18,03	6585
3	54,09	19756

Die folgende Tabelle gibt einen Überblick über die Dauern verschiedener Mondzyklen in einem Saros-Zyklus (18,03 tropische Jahre) sowie in einem dreimal so langen Zyklus Exeligmos-Zyklus (54,09 tropische Jahre) .

	Synodische Perioden	Drakonitische Perioden	Tage	Anomalistische Perioden
Dauer einer Periode in Tagen	29,53059	27,21222	1	27,53455
Anzahl der Perioden im Saros-Zyklus	223	242	6585	239
Anzahl der Tage im Saros-Zyklus	6585,3216	6585,3572	6585,0000	6580,7575
Differenz zu synodischen Perioden in Tagen	0,0000	0,0357	-0,3216	-4,5641
Differenz zu drakonitischen Perioden in Tagen	-0,0357	0,0000	-0,3572	-4,5998
Differenz zu ganzen Tagen	0,3216	0,3572	0,0000	-4,2425
Differenz zu synodischen Perioden in Stunden	0,00	0,86	-7,72	-109,54
Differenz zu drakonitischen Perioden in Stunden	-0,86	0,00	-8,57	-110,39
Differenz zu ganzen Tagen in Stunden	7,72	8,57	0,00	-101,82
Anzahl der Perioden im Exeligmos-Zyklus	669	726	19756	717
Anzahl der Tage im Exeligmos-Zyklus	19755,9647	19756,0717	19756,0000	19742,2724
Differenz zu synodischen Perioden in Tagen	0,0000	0,1070	0,0353	-13,6924
Differenz zu drakonitischen Perioden in Tagen	-0,1070	0,0000	-0,0717	-13,7994
Differenz zu ganzen Tagen in Tagen	-0,0353	0,0717	0,0000	-13,7277
Differenz zu synodischen Perioden in Stunden	0,00	2,57	0,85	-328,62
Differenz zu drakonitischen Perioden in Stunden	-2,57	0,00	-1,72	-331,18
Differenz zu ganzen Tagen in Stunden	-0,85	1,72	0,00	-329,46

Langfristige Beobachtungen

Da sich die Sonne definitionsgemäß immer in der Ekliptikebene befindet, wiederholen sich die Verhältnisse in Bezug auf ihre Auf- und Untergangspunkte sowie auf ihre südlichen und die nördlichen Kulminationshöhen in jedem tropischen Sonnenjahr. Zur Sommersonnenwende steht die Sonne am höchsten und am längsten über den Horizont, die Auf- und Untergangsazimute erreichen ihre nördlichsten Positionen und es ergibt sich der Kalendertag mit dem längsten Tagesslicht und der kürzesten Dunkelheit. Zur Wintersonnenwende steht die Sonne am niedrigsten und am kürzesten über den Horizont, die Auf- und Untergangsazimute erreichen ihre südlichsten Positionen und es ergibt sich der Kalendertag mit dem kürzesten Tagesslicht und der längsten Nacht. Bei den beiden Äquinoktien zum Frühlings- und Herbstbeginn herrscht die Tag-und-Nacht-Gleiche, zwölf Stunden Tag und zwölf Stunden Nacht .Die Sonne geht überall auf der Erde exakt im Osten auf beziehungsweise im Westen unter.

Mit dem Neumond verhält es sich ähnlich wie mit der Sonne, da er sich stets in Sonnennähe befindet. Die Mondbahn ist gegenüber der Ekliptik jedoch geneigt (Inklination der Mondbahn), so dass der Mond bis zu gut 5 Bogengrad höher oder niedriger stehen kann, als die Sonnenscheibe. Bei einer großen Mondwende steht die Ekliptik immer besonders hoch über dem Horizont und der Mond hat gleichzeitig seine maximale nördliche ekliptikale Breite erreicht. Wenn der Vollmond bei einer großen Mondwende auf dem südlichen Meridian kulminiert, findet dieses Ereignis als größte Mondwende um Mitternacht zur Wintersonnenwende statt (im Dezember 2023, 2042 und 2061).

Die Größte Mondwende bei der am höchsten stehenden Ekliptik auf der Nordhalbkugel sowie die Sommersonnenwende im Horizontsystem. Die blaue Mondbahn wird während der Sommersonnenwende nur bei Neumond gleichzeitig mit der orangefarbenen Sonnenbahn durchlaufen. Während der Wintersonnenwende findet diese große Mondwende statt, wenn der Mond in Opposition zur Sonne steht und somit Vollmond herrscht.

Bei einer kleinen Mondwende steht die Ekliptik immer besonders niedrig über dem Horizont und der Mond hat gleichzeitig seine minimale südliche ekliptikale Breite erreicht. Wenn der Vollmond bei einer kleinen Mondwende auf dem südlichen Meridian kulminiert, findet dieses Ereignis als kleinste Mondwende um Mitternacht zur Sommersonnenwende statt (im Juni 2024, 2043 und 2062).

Die kleinste Mondwende bei der am niedrigsten stehenden Ekliptik auf der Nordhalbkugel sowie die Wintersonnenwende im Horizontsystem. Die blaue Mondbahn wird während der Wintersonnenwende nur bei Neumond gleichzeitig mit der orangefarbenen Sonnenbahn durchlaufen. Während der Sommersonnenwende findet diese kleine Mondwende statt, wenn der Mond in Opposition zur Sonne steht und somit Vollmond herrscht.

Sonnenwenden

Der maximale Höhenwinkel über dem Horizont wird bei allen Himmelsobjekten grundsätzlich bei der Kulmination auf dem südlichen Meridian erreicht. Dieser Höhenwinkel ergibt sich aus dem zur Beobachtung gehörenden geographischen Breitengrad $\varphi$ und der Deklination $\delta$, also die Höhe eines Himmelsobjektes über dem Himmelsäquator. Der Zusammenhang zwischen dem maximalen Höhenwinkel auf dem südlichen Meridian $h_{max,S}$ und dem geographischen Breitengrad $\varphi$ der Beobachtung kann mit Hilfe der Deklination $\delta$ wie folgt hergestellt werden:

$h_{max,S}=(90^{\circ }-\varphi )+\delta$

Daraus ergibt sich, dass bei bekannter Deklination $\delta$ aus der Beobachtung des Höhenwinkels $h_{max,S}$ der Breitengrad $\varphi$ bestimmt werden kann:

$\varphi =90^{\circ }+\delta -h_{max,S}$

Ist der Breitengrad $\varphi$ bekannt, kann anhand der Beobachtung des Höhenwinkels ${max,S}$ die Deklination eines Himmelsobjekts $\delta$ bestimmt werden:

$\delta =\varphi +h_{max,S}-90^{\circ }$

Bei den Tag-und-Nacht-Gleichen geht die Sonne genau im Osten auf und genau im Westen unter. Im Laufe eines Jahres pendeln ihre Auf- und Untergangspunkte symmetrisch um diese diese beiden Äquinoktialpunkte. Die Winkel der Auf- und Untergangspunkte können auf dem Horizont mit ihrem Azimut $a$ angegeben werden, wobei die Azimute im horizontalen System von Norden (0 Bogengrad) aus über Osten (90 Bogengrad) nach Süden (180 Bogengrad) und dann weiter nach Westen (270 Bogengrad) gemessen werden:

$a=\arccos {\frac {\sin \delta }{\cos \phi }}$

Anmerkung: Die atmosphärische Refraktion vergrößert den von der Erdoberfläche aus beobachteten Höhenwinkel in der Nähe des Horizonts ein wenig. Dadurch gehen die Gestirne etwas früher auf und gehen etwas später unter als sich aus der hier durchgeführten, rein geometrischen Betrachtungsweise ergibt. Durch die Berücksichtigung der atmosphärischen Refraktion ergeben sich darüber hinaus in Abhängigkeit vom Winkel zwischen der Ekliptiklinie und der Horizontline auch geringfügig abweichende Azimute.

Durch Einsetzen der entsprechenden Deklinationen der Sonne können die maximalen Höhenwinkel bei ihrer Kulmination auf dem südlichen Meridian berechnet werden, wobei $\varepsilon$ für die Schiefe der Ekliptikebene (heute 23,44 Bogengrad) in Bezug auf das äquatoriale System steht: Für die Sonne ergeben sich demnach die in der folgende Tabelle angegebenen Werte:

Deklinationen, maximale Höhenwinkel sowie Auf- und Untergangsazimute der Sonne

Ereignis	Deklination der Sonne $\delta _{S}$	Maximaler Höhenwinkel der Sonne $h_{max,S}$	Azimut des Sonnenaufgangs $a_{A,S}$	Azimut des Sonnenuntergangs $a_{U,S}$
Wintersonnenwende	$-\varepsilon$	$(90^{\circ }-\varphi )-\varepsilon$	$180^{\circ }-\arccos {\frac {\sin \varepsilon }{\cos \varphi }}$	$180^{\circ }+\arccos {\frac {\sin \varepsilon }{\cos \varphi }}$
Tag-und-Nacht-Gleiche	0	$(90^{\circ }-\varphi )$	$90^{\circ }$	$270^{\circ }$
Sommersonnenwende	$+\varepsilon$	$(90^{\circ }-\varphi )+\varepsilon$	$\arccos {\frac {\sin \varepsilon }{\cos \varphi }}$	$360^{\circ }-\arccos {\frac {\sin \varepsilon }{\cos \varphi }}$

Mondwenden

Zunehmender Mond zum Herbst-Äquinoktium bei kleiner Mondwende mit flacher Ekliptik in Berlin mit fast senkrecht stehender Mondsichel (38% beleuchtet) im Sternbild Skorpion kurz vor Sonnenuntergang. Visuelle Helligkeit -9 mag, südliche ekliptikale Breite = -5°, Höhe über dem südlichen Horizont = 9°, Mondalter 6,2 Tage.

In der folgenden Übersicht sind die Mondaufgangspunkte am östlichen Horizont, die Kulminationspunkte auf dem südlichen Meridian und die Monduntergangspunkte am westlichen Horizont für die vier verschiedenen Jahreszeiten angegeben:

Die Lage des Bogens der Ekliptik über dem nächtlichen Horizont zu verschiedenen Jahreszeiten

Jahreszeit	Abends (Aufgang des Vollmonds in östlicher Richtung)	Um Mitternacht (Kulmination des Vollmonds auf dem südlichen Meridian)	Morgens (Untergang des Vollmonds in westlicher Richtung)
Frühlingsanfang Tag-und-Nacht-Gleiche
Sommeranfang Sommersonnenwende
Herbstanfang Tag-und-Nacht-Gleiche
Winteranfang Wintersonnenwende

Im Laufe eines drakonitischen Monats geht der Mond sowohl durch den aufsteigenden als auch durch den absteigenden Knoten (Drachenpunkte) seiner Mondbahn. Nach dem Durchqueren des aufsteigenden Knotens wird die ekliptikale Breite des Mondes positiv (nördliche ekliptikale Breite), er steigt in Bezug zur Ekliptiklinie nach Norden und bleibt entsprechend immer länger über dem Horizont. Nach dem Durchqueren des absteigenden Knotens wird die ekliptikale Breite des Mondes negativ (südliche ekliptikale Breite), er fällt in Bezug zur Ekliptiklinie nach Süden und bleibt entsprechend immer kürzer über dem Horizont. In der deutschsprachigen Schweiz gibt es für diese im Laufe eines drakonitischen Monats täglich mehr oder weniger deutlich wahrnehmbaren Änderungen der ekliptikalen Breite sogar eigene Adjektive. Das Ansteigen der ekliptikalen Breite des Mondes nach Norden wird obsigend, und das Abfallen der ekliptikalen Breite des Mondes nach Süden wird nidsigend genannt.

Verschiedene Mond- und Sonnenwenden auf dem südlichen Meridian im Laufe eines Jahres in Bezug zum Horizontsystem.

Im Laufe der Zeit pendelt der Mond immer wieder zwischen den kleinen und großen Mondwenden. Dieser Ablauf wiederholt sich nach einem vollständigen drakonitischen Zyklus, also nach 18,61 Jahren, innerhalb dessen die kleinste und die größte Mondwende im zeitlichen Abstand von rund 9,3 Jahren jeweils einmal erreicht wird.

Die Deklinationen des Mondes $\delta _{M}$ pendeln also um die Werte der Deklination der Sonne $\delta _{S}$. Die Deklination und der maximale Höhenwinkel bei der Kulmination des Mondes auf dem südlichen Meridian ergeben sich unter Berücksichtigung der Inklination der Mondbahn gegenüber der Ekliptikebene $i$ (heute 5,145 Bogengrad) wie folgt:

Deklinationen des Mondes

Ereignis	Deklination des Mondes $\delta _{M}$	Maximaler Höhenwinkel des Mondes $h_{max,M}$	Azimut des Mondaufgangs $a_{A,M}$	Azimut des Monduntergangs $a_{U,M}$
Kleinste Mondwende	$-(\varepsilon +i)$	$(90^{\circ }-\varphi )-(\varepsilon +i)$	$180^{\circ }-\arccos {\frac {\sin(\varepsilon +i)}{\cos \varphi }}$	$180^{\circ }+\arccos {\frac {\sin(\varepsilon +i)}{\cos \varphi }}$
Kleine Mondwende	$\delta _{S}-i$	$(90^{\circ }-\varphi )+(\delta _{S}-i)$	-	-
Mond im Knoten	$\delta _{S}$	$(90^{\circ }-\varphi )+\delta _{S}$	-	-
Große Mondwende	$\delta _{S}+i$	$(90^{\circ }-\varphi )+(\delta _{S}+i)$	-	-
Größte Mondwende	$+(\varepsilon +i)$	$(90^{\circ }-\varphi )+(\varepsilon +i)$	$\arccos {\frac {\sin(\varepsilon +i)}{\cos \varphi }}$	$360^{\circ }-\arccos {\frac {\sin(\varepsilon +i)}{\cos \varphi }}$

Die für die Azimute anzuwendenden Formeln hängen vom Vorzeichen der Deklination des Mondes $\delta _{M}$ ab. Bei den kleinen Mondwenden, bei den großen Mondwenden und zu den Zeiten, wenn sich der Mond in seinen Knoten befindet, können die Azimute entsprechend den Verhältnissen bei den anderen Formeln berechnet werden.

Die maximalen Höhenwinkels des Mondes und der Sonne konnten zum Beispiel schon in der Bronzezeit mit Hilfe von Stabdolchen beobachtet und bestimmt werden.

Siehe hierzu auch Stabdolche.

Zyklen

Die folgenden Periodendauern spielen bei Sonnen- und Mondzyklen eine besondere Rolle:

• Meton-Zyklus:
  • 19 tropische Sonnenjahre = 6939,6 Tage, bestimmt durch die ekliptikale Länge der Sonne in Bezug zum Frühlingspunkt mit ihren Äquinoktien und Sonnenwenden.
  • 235 synodische Monate = 6939,7 Tage, bestimmt durch die Mondphasen mit Neumonden und Vollmonden.
  • 254 siderische Monate = 6939,7 Tage, bestimmt durch die ekliptikale Länge des Mondes in Bezug zum Frühlingspunkt und den Fixsternhimmel.
  • 255 drakonitische Monate = 6939,1 Tage, bestimmt durch die ekliptikale Breite des Mondes beziehungsweise die auf- und absteigenden Knoten der Mondbahn.
• Drakonitischer Zyklus:
  • 249,83 drakonitische Monate = 6798,38 Tage = 18,61 tropische Sonnenjahre, bestimmt durch die ekliptikalen Längen der auf- und absteigenden Knoten der Mondbahn: Zyklus der Mondwenden und Sternbedeckungen
• Saros-Zyklus:
  • 242 drakonitische Monate = 6585,3 Tage = 18,03 tropische Sonnenjahre (respektive 18 Jahre und 11 Tage): Zyklen der Sonnen- und Mondfinsternisse
  • 223 synodische Monate = 6585,4 Tage, bestimmt durch die Mondphasen mit Neumonden und Vollmonden.

Der 19-jährige Meton-Zyklus vom Januar 2023 bis zum Januar 2042. Die Zeit schreitet in horizontaler Richtung jeweils um einen halben Tag pro Bildpunkt voran.
Im unteren Teil des Diagramms sind die kleinen und großen Mondwenden für die geographische Breite 52,5 Bogengrad (zum Beispiel in Berlin) dargestellt.

Herbstäquinoktium (orange) und Sonnenfinsternis bei aufsteigendem (rot) Neumond am 23. September 2033 (orangefarbene Linie), Mondfinsternis bei absteigendem (blau) Vollmond am 8. Oktober 2033 und Wintersonnenwende (türkis) mit kleiner Mondwende bei Neumond am 21. Dezember 2033 (grüne Linie).

Der Vollmond (weiß) erscheint sowohl zu Beginn der Darstellung am 6. Januar 2023 als auch nach genau 19 Jahren am 6. Januar 2042. Dieser Sachverhalt ergibt sich daraus, dass nach dem Durchlauf eines Meton-Zyklus eine ganzzahlige Anzahl von 235 synodischen Perioden durchlaufen wird (gleiche Elongation des Mondes). Diese Vollmonde stehen bei der gleichen ekliptikalen Länge im Sternbild Zwillinge (Gemini). Dieser Sachverhalt ergibt sich daraus, dass nach dem Durchlauf eines Meton-Zyklus eine ganzzahlige Anzahl von 254 siderischen Perioden durchlaufen wird. Gleichzeitig steht auch die Sonne nach 19 tropischen Sonnenjahren auf dem Zodiak bei der gleichen ekliptikalen Länge und somit erneut genau gegenüber vom Mond im Sternbild Schütze (Sagittarius). Da die Meton-Periode nur gut einen halben Tag länger ist als 255 drakonitische Perioden, stehen diese beiden Vollmonde bei fast der gleichen ekliptikalen Breite nördlich vom Stern Mebsuta (ε Geminorum).

Große Mondwenden mit maximaler Höhe des Mondes und längstem Bogen über dem Horizont folgen stets dem aufsteigenden Mondknoten (rot), und kleine Mondwenden mit minimaler Höhe des Mondes und kürzestem Bogen über dem Horizont folgen stets dem absteigenden Mondknoten (blau).

Kleinste Mondwende um die Mittsommernacht 2024:Der Vollmond (scheinbarer Durchmesser = 31,8 Minuten) am 23. Juni 2024 nach ein Uhr und kurz vor der oberen Kulmination auf dem südlichen Meridian von Berlin-Lankwitz (nördliche geographische Breite = 52,44 Bogengrad) aus gesehen. Die ekliptikale Breite hatte einen Minimalwert, der fast 6 Bogengrad südliche Breite betrug und somit zu einer extrem geringen maximalen Höhe über dem Horizont von nur 8,5 Bogengrad führte.Im norwegischen Trondheim (nördliche geographische Breite = 63,44 Bogengrad, also drei Breitengrade südlich vom nördlichen Polarkreis) oder im isländischen Reykjavik (nördliche geographische Breite = 64,15 Bogengrad) war in diesen Tagen weder die Mitternachtssonne noch der Vollmond zu sehen.Der helle Stern rechts oberhalb der Mondscheibe ist Nunki im Schützen (σ Sagittarius, visuell 2,7^m), unterhalb ist Asella (ζ Sagittarius, visuell 4,2^m) zu sehen.

Die größte Mondwende bei Vollmond tritt stets zur Wintersonnenwende und die kleinste Mondwende bei Vollmond tritt stets zur Sommersonnenwende auf. Je nach ekliptikaler Breite des Mondes schwanken die absoluten Werte für die Horizontwinkel um das doppelte der Inklination der Mondbahn, das heißt um bis zu 10,29 Bogengrad. Die ekliptikale Breite bezieht sich auf den Erdmittelpunkt, da dieser in der Ekliptikebene liegt. Die von der Erdoberfläche aus beobachtete ekliptikale Breite des im Mittel nur zirka 383100 Kilometer entfernten Mondes hängt zusätzlich vom jeweiligen geographischen Breitengrad der Beobachtung ab. Der Nordpol und der Südpol liegen um den Polradius von 6357 Kilometer oberhalb (nördlich) beziehungsweise unterhalb (südlich) der Ekliptikebene. Daraus resultiert für die beobachtete ekliptikale Breite ein zusätzlicher Winkel von:

$\Delta \beta =\arctan {\frac {6357}{383100}}\approx \pm 0,95^{\circ }$

Die größte Mondwende bei Vollmond (weiß) tritt bei maximaler ekliptikaler Breite des Mondes um die Wintersonnenwende (türkis, siehe Dezember 2023) auf. Die kleinste Mondwende bei Vollmond (weiß) tritt bei minimaler ekliptikaler Breite des Mondes um die Sommersonnenwende (gelb, siehe Juni 2024).

In dem 19-jährigen Diagramm (siehe oben) ist gut zu erkennen, wie sich die Konstellation zwischen Mondknoten (rot und blau) und Mondphasen (weiß und schwarz) nach den 19 Jahren des Meton-Zyklus wiederholt (vergleiche Januar 2023 und Januar 2042).

Der erste aufsteigende Mondknoten (rot) wird fünf Tage vor Vollmond am 2. Januar 2023 erreicht. Nach einer vollständigen Saros-Periode von 18 Jahren und 11 Tagen, also am 12. Januar 2041 wird fünf Tage vor Vollmond ebenfalls wieder ein aufsteigender Mondknoten erreicht.

Eine Besonderheit gibt es im März 2038: Die Tag-und-Nacht-Gleiche erfolgt bereits am 20. März 2038 (Samstag) und der erste Frühlingsvollmond nur einige Stunden später am 21. März 2038 (Sonntag). Grundsätzlich müsste also der darauffolgende Sonntag, nämlich der 28. März 2038, das Osterdatum sein. In diesem Fall greift die abweichende Regel, dass erst der Vollmond nach dem 21. März als Frühlingsvollmond zu rechnen ist, was erst am 19. April 2038 (Montag) der Fall ist. Demzufolge ist das Osterdatum auf den 25. April 2038 (Sonntag) festgelegt.

Eine Sonnenfinsternis tritt immer dann auf, wenn ein Neumond (weiß) zeitnah durch einen aufsteigenden (rot) oder absteigenden (blau) Mondknoten läuft. Dies ist im obigen Diagramm an den folgenden Tagen der Fall:

• 20. April 2023, 14. Oktober 2023, 8. April 2024, 2. Oktober 2024, 29. März 2025, 21. September 2025 (Herbstäquinoktium), 17. Februar 2026, 12. August 2026, 6. Februar 2027, 2. August 2027, 26. Januar 2028, 22. Juli 2028, 14. Januar 2029, 12. Juni 2029, 11. Juli 2029, 5. Dezember 2029, 1. Juni 2030, 25. November 2030, 21. Mai 2031, 14. November 2031, 9. Mai 2032, 3. November 2032, 30. März 2033, 23. September 2033 (Herbstäquinoktium), 20. März 2034 (Frühlingsäquinoktium), 12. September 2034, 9. März 2035, 2. September 2035, 27. Februar 2036, 23. Juli 2036, 21. August 2036, 16. Januar 2037, 13. Juli 2037, 5. Januar 2038, 2. Juli 2038, 26. Dezember 2038, 21. Juni 2039 (Sommersonnenwende), 15. Dezember 2039, 11. Mai 2040, 4. November 2040, 30. April 2041, 25. Oktober 2041

Genau neunzehn Jahre nach den ersten beiden genannten Sonnenfinsternissen im Jahr 2023 treten an den gleichen Kalendertagen erneut zwei Sonnenfinsternisse auf, nämlich am 20. April 2042 und am 14. Oktober 2042.

Neunzehn Jahre vor den sechs ersten aufgeführten Sonnenfinsternissen in den Jahren 2023 bis 2025 traten an fast immer den gleichen Kalendertagen ebenfalls Sonnenfinsternisse auf, nämlich am 19. April 2004, am 14. Oktober 2004, am 8. April 2005, am 3. Oktober 2005, am 29. März 2006 und am 22. September 2006.

Eine Mondfinsternis tritt immer dann auf, wenn ein Vollmond (weiß) zeitnah durch einen aufsteigenden (rot) oder absteigenden (blau) Mondknoten läuft. Dies ist im obigen Diagramm an den folgenden Tagen der Fall:

• 5. Mai 2023, 28. Oktober 2023, 25. März 2024, 18. September 2024, 14. März 2025, 7. September 2025, 3. März 2026, 28. August 2026, 20. Februar 2027, 18. Juli 2027, 17. August 2027, 12. Januar 2028, 6. Juli 2028, 31. Dezember 2028, 26. Juni 2029, 20. Dezember 2029 (Wintersonnenwende), 15. Juni 2030, 9. Dezember 2030, 7. Mai 2031, 5. Juni 2031, 30. Oktober 2031, 25. April 2032, 18. Oktober 2032, 14. April 2033, 8. Oktober 2033, 3. April 2034, 28. September 2034, 22. Februar 2035, 19. August 2035, 11. Februar 2036, 7. August 2036, 31. Januar 2037, 27. Juli 2037, 21. Januar 2038, 17. Juni 2038 (Sommersonnenwende), 16. Juli 2038, 11. Dezember 2038, 6. Juni 2039, 30. November 2039, 26. Mai 2040, 18. November 2040, 16. Mai 2041, 8. November 2041

• Finsternisse
• 
  Die Finsternisse im Jahr 2025 liegen in der Nähe der Tag-und-Nacht-Gleichen, wo mittlere Mondwenden vorliegen. Der Mond geht im Osten auf und im Westen unter.
• 
  Die Finsternisse im Jahr 2029 liegen in der Nähe der Sonnenwenden. Bei der Sonnenfinsternis im Juni kommt es bei Neumond zu einer großen Mondwende, und bei der darauffolgenden Mondfinsternis kommt es bei Vollmond zu einer kleinen Mondwende. Bei der Sonnenfinsternis im Dezember kommt es bei Neumond zu einer kleinen Mondwende, und bei der darauffolgenden Mondfinsternis kommt es bei Vollmond zu einer großen Mondwende.

Der Kalenderstein vom Tempel Mnajdra

Auf Malta wurde im Hypogäum von Ħal-Saflieni beim Ort Tarxien ein annähernd kreisrunder Stein aus der Tempelperiode der Insel mit zirka sechs Zentimeter Durchmesser gefunden, der wie die Darstellung einer Vollmondscheibe aussieht. Im maltesischen Tempel Mnajdra sind an der südlichen Küste Maltas zirka zehn Kilometer entfernt davon zwei große Kalendersteine gefunden worden, die ebenfalls aus dieser Zeit stammen.

• Die Ruinen der Tempelanlage von Mnajdra
• 
  Plan der Tempelanlage. Die beiden Kalendersteine befinden sich in der Mitte des Urtempels im Osten der Anlage (Buchstabe "A"), die aus den vierten vorchristlichen Jahrtausend stammt.
• 
  Modell der Tempelanlage im Park "Mini-Europa" in Brüssel. Die Kalendersteine befinden sich links und rechts hinter der Frauenfigur auf der rechten Seite.
• 
  Darstellung der Lochreihen der beiden Kalendersteine auf einer Schautafel der archäologischen Stätte.
• 
  Blick vom Eingang des Osttempels auf die beiden aufrecht stehenden Kalendersteine – links der westliche und rechts der östliche Kalenderstein.
• 
  Blick über die Kalendersteine – links der östliche und rechts der westliche Kalenderstein, den Eingang des Osttempels und die Südküste Maltas auf das Mittelmeer mit der vorgelagerten Insel Filfla.

Auf dem östlichen Kalenderstein gibt es mehrere Lochreihen, deren Lochzahlen alle mit lunaren und solaren Kalendern in Zusammenhang gebracht werden können. In der heute zusammengestellten Anordnung der Steine können nicht alle Löcher gebohrt worden sein, da diese teilweise von anderen Steinen verdeckt sind. Die Bohrungen sind heute in horizontaler Richtung ausgerichtet, wurden damals vermutlich unter Ausnutzung der Gravitation senkrecht nach unten auf dem noch liegenden Stein ausgeführt. In dieser Ausrichtung des Steins wäre es auch leicht möglich gewesen, für Markierungs- oder Zählzwecke zum Beispiel kugelförmige Gegenstände in die Löcher zu legen. Steckkalender aus Stein mit Bohrungen (bei den Griechen hießen sie Parapegmata) waren im Altertum an vielen Orten in Verwendung.

Am Kopf des Steins gibt es mehrere hundert, flächenhaft angeordnete Löcher, die eventuell für die einzelnen Monate oder Jahre einer langfristigen Beobachtung stehen. Darunter tauchen rechtsbündig sieben horizontale Lochreihen auf, die in der Skizze mit den Buchstaben A bis G gekennzeichnet sind, wobei die beiden Teilreihengruppen B1 und B2 sowie C1, C2 und C3 zusammengefasst betrachtet werden:

Skizze der Lochreihen auf dem Kalenderstein von Mnajdra nach Ventura und Hoskin.

Lochreihen auf dem östlichen Kalenderstein vom Tempel Mnajdra auf Malta

Reihe	Anzahl der Löcher	Mögliche Verwendung
A	19	Für die jeweilige Goldene Zahl jedes Sonnenjahres innerhalb des 19-jährigen Meton-Zyklus (235 synodische, 255 drakonitische, 254 siderische Monate beziehungsweise 6940 Tage). Nach einem Sonnenjahr hat die Sonne wieder die gleiche ekliptikalen Länge. Nach Ablauf der gesamten Meton-Periode hat der Mond wieder die gleiche Mondphase und die gleiche ekliptikalen Breite und die gleiche ekliptikalen Länge (zum Beispiel im Goldenen Tor der Ekliptik oder im Frühlingspunkt).
B	B1: 13 (links)	In Summe 29, für die Anzahl der vollständigen Tage in einem synodischen Monat (29,5 Tage). Nach dieser Zeit hat der Mond wieder die gleiche Mondphase erreicht. Vom Altlicht des Mondes bis zum Vollmond sind es 16 Tage, und danach sind es 13 Tage bis zum nächsten Altlicht. Nachdem die Doppelreihe vervollständigt wurde, gibt es dafür einen Übertrag in die Reihe E und wenn diese bereits voll ist, für das nächste beginnende Jahr mit der nächstfolgenden Goldenen Zahl einen Übertrag in die Reihe A.
	B2: 16 (rechts darunter)
C	C1: 3 (rechts oben)	Für die sieben vollständigen Tage eines Mondviertels (≈7,4 Tage) respektive einer Woche. Wenn diese Doppelreihe gefüllt ist, gibt es für die Vervollständigung einer neuen Woche einen Übertrag in die Reihe G für die Wochen in einem Jahr. Alternativ könnten hier jeweils die drei Monate in den vier Jahreszeiten markiert und gezählt worden sein. Ein weiterer Zusammenhang besteht eventuell mit der Tatsache, dass in 19 Jahren (siehe Reihe A) sieben synodische Schaltmonate erforderlich sind, um in einem lunisolaren Kalender den Lauf von Sonne und Mond bis auf wenige Stunden genau zu synchronisieren (siehe hierzu auch Plejaden-Schaltregeln).
	C2: 4 (rechts unten)
	C3: 3 (links)	Für die drei nach Neumond vollendeten Mondviertel innerhalb eines laufenden synodischen Monats. Beim Erreichen eines Neumonds, eines abnehmenden Halbmonds, eines Vollmonds oder eines abnehmenden Halbmonds gibt es jeweils einen Übertrag in die Reihe D oder in die Reihe F (siehe unten).
D	25	Für die 25 vollendeten Mondviertel in der ersten Hälfte eines Sonnenjahres, oder entweder für alle zunehmenden Mondviertel (wenn der Mond zu Beginn des Jahres zunehmend war) oder für alle abnehmenden Mondviertel (wenn der Mond zu Beginn des Jahres abnehmend war) eines Sonnenjahres (vergleiche Reihe F).
E	11	Nachdem die Doppelreihe B vollständig durchlaufen wurde, gibt es einen Übertrag in diese Reihe. Diese elf Mulden stehen dann für überzähligen Tage in einem Sonnenjahr (365,2 Tage) im Vergleich zu zwölf synodischen Monaten (354,4 Tage). Wenn diese Reihe bereits voll ist, gibt es für das nächste beginnende Jahr mit der nächstfolgenden Goldenen Zahl einen Übertrag in die Reihe A.
F	24 + 1 = 25	Für die 24 bis 25 vollendeten Mondviertel in der zweiten Hälfte eines Sonnenjahres, oder entweder für alle abnehmenden Mondviertel (wenn der Mond zu Beginn des Jahres zunehmend war) oder für alle zunehmenden Mondviertel (wenn der Mond zu Beginn des Jahres abnehmend war) eines Sonnenjahres (vergleiche Reihe D). Das 25. Loch ist etwas abgesetzt, da es für ein am Ende des Jahres eingeschaltetes 50. Mondviertel (Dauer = 7,38265 Tage) steht, das nur in ungefähr jedem zweiten Sonnenjahr auftritt: 49 x 7,38265 Tage ≈ 361,75 Tage beziehungsweise 50 x 7,38265 Tage ≈ 369,13 Tage 365,242 Tage - 361,75 Tage ≈ 3,5 Tage beziehungsweise 365,242 Tage - 369,13 Tage ≈ -3,9 Tage
G	53	Für die begonnenen 53 Siebentagewochen in einem Sonnenjahr (Dauer = 365,242 Tage) beziehungsweise von einem heliakischen Auf- oder akronychischen Untergang der Plejaden zum nächsten.

Über dem östlichen Horizont beim Morgenletzt gerade noch sichtbares Altlicht des abnehmenden Mondes 33 Stunden vor Neumond mit der vom Erdschein beleuchteten Nachtseite des Mondes. Die Aufnahme entstand kurz vor Herbstbeginn, als die Ekliptik morgens fast senkrecht auf dem Horizont stand.

Zu der Doppelreihe B sei angemerkt, dass auch im altägyptischen Mondkalender, der im Neolithikum in Verwendung war, der Monat nicht mit dem unsichtbaren Neumond, sondern mit dem gerade noch sichtbaren Altlicht des Morgenletztes des Mondes begann, also gut einen Tag vor Neumond. Die beiden letzten Löcher sind etwas nach links abgesetzt, was mit folgendem Sachverhalt im Einklang steht: zwei Tage vor dem Ende einer synodischen Periode, also schon nach gut 27 Tagen, ist ein siderischer Monat vorüber, nach welchem der Mond die gleiche ekliptikale Länge erreicht hat. Das heißt bereits nach gut 27 Tagen steht der Mond zum Beispiel wieder im Goldenen Tor der Ekliptik, bevor er erst nach gut 29 Tagen erneut sein Altlicht erreicht (gut einen Tag vor Neumond). Die Sonne ist innerhalb des synodischen Monats durch die Bewegung der Erde um die Sonne gegenüber dem Fixsternhimmel um knapp 30 Bogengrad weiter nach links gezogen.

Die 25 Wochen des abnehmenden Mondes werden zum Beispiel auch im 79. Kapitel des ungefähr 2000 Jahre alten  äthiopischen Henochbuches erwähnt. Alternativ könnten die 50 Löcher in Reihen D und F eventuell auch für die 50 vollständigen Siebentagewochen (350 Tage) innerhalb von zwölf synodischen Perioden stehen, die eine Dauer von 50,6 Wochen beziehungsweise 354,4 Tagen haben.

Zur Zahl Elf (Reihe E) ist noch festzuhalten, dass die Erde innerhalb eines siderischen Jahres des Planeten Jupiter (zwölf Erdenjahre) elf Mal mit diesem in Opposition steht. Zu diesen Zeitpunkten ist der Abstand zwischen Erde und Jupiter am geringsten, der Jupiter hat steht in seinem größten Glanz und er kulminiert um Mitternacht auf dem südlichen Meridian.

Detail des westlichen Kalendersteins aus dem Osttempel von Mnajdra.

Auch auf einem weiteren, sogenannten westlichen und heute ebenfalls aufgerichteten Stein der Tempelanlage sind mehrere Lochreihen zu sehen, die aus 16, 12, 19, 7, 30, 31, 32, 35, 37, 12 und 13 Löchern bestehen. Einige dieser Zahlen tauchen auch im Zusammenhang mit dem östlichen Stein auf oder sind ebenfalls leicht mit lunaren oder solaren Kalendertagen in Verbindung zu bringen:

• 16: Anzahl der Tage vom Altlicht bis zum Vollmond.
• 12: Anzahl der vollständigen Monate pro Jahr.
• 19: Anzahl der tropischen Jahre pro Meton-Periode.
• 7: Anzahl der vollständigen Tage pro Mondviertel respektive der Tage pro Woche.
• 30: aufgerundete Anzahl der Tage pro synodischer Periode respektive der Tage pro Monat.

→ In Bezug auf die Bedeutung von bestimmten Zahlen in der Astronomie siehe auch Exkurs „Zahlen“.

Malereien in der Höhle von Magura

In der schon im Neolithikum genutzten Magura-Höhle im Nordwesten des heutigen Bulgariens gibt es nicht nur eine sehr alte bildliche Darstellung eines Schöpfungsmythos, sondern ebenfalls Hinweise darauf, dass verschiedene Mondzyklen bekannt waren. Unter den Darstellungen befindet sich insbesondere eine Reihe von Strichen, mit denen die 16 Tage vom Altlicht des Mondes bis zu Vollmond gezählt worden sein können.

→ Weitere Erläuterungen finden sich im Wikibook „Die Höhlenmalerei in der Magura-Höhle“.

Erste Hälfte des synodischen Monats in einer Darstellung der Höhlenmalerei von Magura. Rechts ist die schmale, liegende Mondsichel des Altlichts beim Morgenletzt zu sehen. Ein bis zwei Tage später ist Neumond, danach nimmt der Mond wieder zu, und nach insgesamt sechzehn Tagen wird der Vollmond erreicht (links).

Kontrastverhältnisse bei aschgrauem Mondlicht

Die vom Erdschein beleuchtete Nachtseite des Mondes wird neben der schmalen Mondsichel (11 Prozent, Mondalter = 3,3 Tage) mit aschgrauem Mondlicht sichtbar. Aufnahme über dem westlichen Abendhimmel kurz nach dem Äquinoktium im Frühjahr bei besonders steiler Ekliptik von Berlin aus gesehen. Links der Stern Omikron Arietis (37 Ari, 6,2^m) im Sternbild Widder.

Das aschgraue Mondlicht kann wenige Tage vor und nach Neumond im Schattenbereich des Mondes beobachtet werden, wenn die Sonne unter dem Horizont steht. Der Schattenbereich wird hierbei durch den Erdschein beleuchtet und hebt sich deutlich sichtbar vom Himmel ab, der den Mond umgibt. Der Erdschein hängt vom Albedo der vom direkten Sonnenlicht getroffenen Erde ab und kann insbesondere durch den Anteil an Wolken in der Atmosphäre sowie an Eis- und Schneeflächen auf der Erdoberfläche schwanken. Bereits die Babylonier haben im sechsten vorchristlichen Jahrhundert diesen visuellen Effekt in bildlichen Darstellungen auf Steinreliefs mit dem König Nabonid vor der Mondsichel mit aschgrauem Licht festgehalten:

• 
  Darstellung der letzten Königs des Neubabylonischen Reiches, Nabonid, vor der Mondsichel mit aschgrauem Licht am Kopf einer babylonischen Stele aus Harran im Archäologischen Museum Şanlıurfa in der Türkei aus dem sechsten vorchristlichen Jahrhundert.
• 
  Darstellung der letzten Königs des Neubabylonischen Reiches, Nabonid, vor der Mondsichel mit aschgrauem Mondlichts am Kopf einer babylonischen Stele im Britischen Museum.
• 
  Darstellung der Mondsichel mit einem Gesicht im Schattenbereich des Mondes im astronomischen Abschnitt des Voynich-Manuskripts aus dem 15. Jahrhundert.
• 
  Zwei Männer am Abend bei der Betrachtung des Neulichts von Caspar David Friedrich (1819/1820), Öl auf Leinwand, Albertinum, Dresden. Eine in dieser Darstellung ähnliche Konstellation zwischen einer solchen Mondsichel und dem Planeten Jupiter fand am Abend des 28. Märzes 1811 im Sternbild Stier (Taurus) statt. Eine Woche nach der Tag-und-Nacht-Gleiche des Frühjahrs stand der Mond wie im Bild dargestellt mit stark geneigter Sichel etwas tiefer als der Jupiter über dem westlichen Horizont.

Altlicht des Mondes am 3. November 2021 mit aschgrauem Licht im Schattenbereich des Mondes von Berlin aus gesehen.

Das nebenstehende Bild des Altlichts (Mondalter 27,7 von 29,5 Tagen) im Sternbild Jungfrau wurde am 3. November 2021 um 7:05 Uhr morgens mit einem hochwertigen Teleobjektiv mit guter Kontrastübertragung über dem ostsüdöstlichen Horizont (Azimut 122 Bogengrad) in Berlin aufgenom­men. Die Sonne stand zum Zeitpunkt der Aufnahme noch gut ein Bogengrad unter dem Hori­zont, der Mond hatte eine nördliche ekliptikale Breite von gut 3 Bogengrad und eine Elongation von 22 Bogengrad, so dass er bei wolkenlosem Himmel und bei einer Höhe von 17,5 Bogengrad über dem Horizont gut zu beobachten war. Die Mondscheibe war mit bloßem Auge vollständig sichtbar und war zu 3,7 Prozent vom direkten Sonnenlicht beleuchtet.

Die aufgenommenen Rohdaten wurden für diese Auswertung mit einer Software mit mög­lichst neutralen Einstellungen zu einer Schwarz-Weiß-Aufnahme entwickelt (Kontrast = 1, Gamma = 1, Farbtemperatur = 4100 Kelvin, Farbsättigung = 0). Anhand der Bilddaten können die Luminanzwerte (Helligkeiten) im Bild bestimmt werden, um aus beliebigen paarweisen Luminanzwerten den jeweiligen Kontrast zu berechnen. Der Michelson-Kontrast $M$ (auch Modulation), der sich aus zwei benachbarten Luminanzwerten $L_{2}$ und $L_{1}$ ergibt (Bedingung: $L_{2}\geq L_{1}\geq 0$), liegt immer zwischen 0 ($L_{2}=L_{1}$, also kein Kontrast) und 1 beziehungsweise 100 Prozent ($L_{1}=0$, also maxi­maler Kontrast):

$M={\frac {L_{2}-L_{1}}{L_{2}+L_{1}}}$

→ Siehe auch Wikibook Digitale bildgebende Verfahren, Kapitel Grundlagen, Abschnitt Modulation.

Die Sichel ist in der ausgewerteten Aufnahme nicht überbelichtet, hat im Scheitel einen mittleren Luminanzwert von:

$L_{Sichel}=236$

Der den Mond umgebende Himmel hat durch das vorhandene Streulicht in der Troposphäre einen mittleren Luminanzwert von:

$L_{Himmel}=15$

Daraus resultiert ein entsprechend hoher Michelson-Kontrast $M$:

$M_{Sichel,Himmel}={\frac {L_{Sichel}-L_{Himmel}}{L_{Sichel}+L_{Himmel}}}={\frac {236-15}{236+15}}={\frac {221}{251}}=0,88$

Im aschgrauen Licht in der Schattenseite des abnehmenden Mondes (dessen gesamte scheinbare Helligkeit beträgt bei der in der Abbildung sichtbaren Mondphase übrigens ungefähr -3^m), die vom Erdschein beleuchtet wird, ergibt sich für die etwas variierende Reflektivität der Mondoberfläche ein mittlerer Luminanzwert von:

$L_{Schatten}=24,5$

Im Vergleich zur hellen Mondsichel ergibt sich daraus ein etwas geringerer Kontrast zwischen Mondsichel und Mondschatten als zwischen Mondsichel und Nachthimmel:

$M_{Sichel,Schatten}={\frac {L_{Sichel}-L_{Schatten}}{L_{Sichel}+L_{Schatten}}}={\frac {236-24,5}{236+24,5}}={\frac {211,5}{260,5}}=0,81$

Die Standardabweichung beträgt in der Schattenseite des abnehmenden Mondes:

$L_{Abweichung}=2,5$.

Innerhalb der sichtbaren Schattenseite des Mondes resultiert aus den dort mit einer Standardabweichung um den Mittelwert herum auftretenden Luminanzwerten für das aschgraue Licht ein Kontrast von nur 10 Prozent:

$M_{Schatten}={\frac {(L_{Schatten}+L_{Abweichung})-(L_{Schatten}-L_{Abweichung})}{(L_{Schatten}+L_{Abweichung})+(L_{Schatten}-L_{Abweichung})}}={\frac {L_{Abweichung}}{L_{Schatten}}}={\frac {2,5}{24,5}}=0,10$

Dieser Kontrastwert ergibt sich im Übrigen im gleichen Maße auch auf der von der Sonne voll beleuchteten und dann jedoch insgesamt erheblich helleren Oberfläche des Vollmonds (die scheinbare Helligkeit beträgt dann ungefähr -13^m).

Anmerkung: Die Sinnhaftigkeit der Kontrastbestimmung mit der Standardabweichung begründet sich in der Tatsache, dass eine perfekte schwarz-weiße Kante mit einem maximalen Luminanzwert $L_{max}$ im hellen Bereich und einem Luminanzwert von Null im dunklen Bereich eine Modulation $M$ von eins hat, sofern die weiße und die schwarze Teilfläche gleich groß sind und jeweils ${\frac {n}{2}}$ Messwerte beinhalten. Sowohl der Mittelwert aller $n$ Luminanzwerte als auch die Standardabweichung aller $n$ Luminanzwerte sind dann beide genau halb so groß wie der maximale Luminanzwert:

$L_{Mittelwert}=\sum _{i=1}^{n}L_{i}=\sum _{i=1}^{\frac {n}{2}}0+\sum _{i=1}^{\frac {n}{2}}L_{max}={\frac {L_{max}}{2}}$

$L_{Standardabweichung}={\sqrt {\frac {\sum _{i=1}^{n}(L_{i}-L_{Mittelwert})^{2}}{n}}}={\sqrt {\frac {\sum _{i=1}^{n}\left({\frac {L_{max}}{2}}\right)^{2}}{n}}}={\sqrt {\frac {n\cdot \left({\frac {L_{max}}{2}}\right)^{2}}{n}}}={\frac {L_{max}}{2}}$

Der Mittelwert zuzüglich der Standardabweichung entspricht dann dem maximalen Luminanzwert:

$L_{Mittelwert}+L_{Standardabweichung}={\frac {L_{max}}{2}}+{\frac {L_{max}}{2}}=L_{max}$

Und der Mittelwert abzüglich der Standardabweichung hat dann den Wert Null:

$L_{Mittelwert}-L_{Standardabweichung}={\frac {L_{max}}{2}}-{\frac {L_{max}}{2}}=0$

Der auf diesem Weg bestimmte Kontrast stimmt mit dem oben genannten Kontrast an der Kante überein:

$M={\frac {L_{max}-0}{L_{max}+0}}={\frac {L_{max}}{L_{max}}}=1$

Schließlich kann auch noch der Kontrast an der Außenkante der nur vom Erdschein beleuch­teten Mondscheibe bestimmt werden, also zwischen aschgrauem Mondlicht und Himmel:

$M_{Schatten,Himmel}={\frac {L_{Schatten}-L_{Himmel}}{L_{Schatten}+L_{Himmel}}}={\frac {24,5-15}{24,5+15}}={\frac {9,5}{39,5}}=0,24$

Dieser Kontrast ist also deutlich höher als der innerhalb des Mondschattenbereichs. Die Helligkeit wechselt an der Kante der Mondscheibe zudem schlagartig und ist deswegen besser wahrnehmbar als die Helligkeitsunterschiede innerhalb des Schattenbereiches, wie im Folgenden ausgeführt wird.

Kontrastempfindlichkeitsfunktion (englisch: Contrast Sensitivity Function, CSF) des menschlichen Auges über der Ortsfrequenz $f_{a}$ in Linienpaaren pro Grad.

Strukturen, bei denen sich die Helligkeit innerhalb eines achtel Bogengrades (7,5 Bogen­minuten) ändert, werden von einem gesunden menschlichen Auge nahezu perfekt auf die Netzhaut übertragen und sind deshalb am besten wahrzunehmen. Weichere Strukturen mit sich langsamer und kontinuierlich ändernder Helligkeit oder kleinere Strukturen sind bei gleichem Objektkontrast schwieriger zu erkennen. Ob ein bestimmter Objektkontrast mit bloßem Auge wahrgenommen werden kann, kann mit Hilfe der Kontrastempfindlichkeits­funktion (Contrast Sensitivity Function (CSF)) des menschlichen Auges ermittelt werden, bei der die Kontrastübertragung von einem Objekt auf die Netzhaut des Auges über der Ortsfrequenz in Linienpaaren pro Bogengrad angegeben ist:

→ Siehe auch Wikibook Digitale bildgebende Verfahren, Kapitel Grundlagen, Abschnitt Kontrastempfindlichkeitsfunktion.

Zur Kontrastempfindlichkeitsfunktion des menschlichen Auges mit den Ortsfrequenzen von 2 sinusmodulierten Linienpaaren pro Bildbreite (linke Bildhälfte) bis hin zu 1024 Linienpaaren pro Bildbreite (rechts am Bildrand), Bildgröße 3860 mal 2160 Bildpunkte (16:9) mit maximalem Kontrast unten, ohne Kontrast oben.

Das nebenstehende Diagramm und die darunter befindliche unfarbige Graphik mit den sinusförmigen Helligkeitsmodulationen visualisieren dies. Von links nach rechts wächst die Ortsfrequenz ausgehend von zwei Linienpaaren pro Bildbreite immer weiter, und der Kontrast ändert sich in vertikaler Richtung kontinuierlich zwischen den Extremwerten 0 und 1. Bei großen und sehr kleinen Ortsfrequenzen sind geringe Kontraste nicht so gut zu erkennen wie im mittleren Bereich. Die maximale Empfindlichkeit wird bei acht Linienpaaren pro Bogengrad erreicht und hängt bei einem gegebenen Objekt demzufolge vom Betrachtungsabstand ab.

Das Auge kann nach dieser Kontrastempfindlichkeitsfunktion innerhalb eines Bogengrades maximal bis zu 80 Linien mit maximalem Objektkontrast (also 40 Linienpaare mit dem Kontrast 1) wahrnehmen. In diesem Fall liegt der wahrgenommene Kontrast zwischen den benachbarten Linien bei ungefähr 5 Prozent. Bei 120 Linien mit maximalem Objektkontrast (also 60 Linienpaare mit dem Kontrast 1) sinkt der wahrgenommene Kontrast auf unter ein Prozent und ist somit praktisch nicht mehr wahrnehmbar. Wegen des scheinbaren Winkeldurchmessers der Mondscheibe von 0,5 Bogengrad, kann das Auge innerhalb des Monddurchmessers also maximal 20 Linienpaare beziehungsweise 40 Linien unterscheiden. Insbesondere an der scharfen Kante der Mondscheibe ist eine ins Auge nahezu verlustfrei übertragene Ortfrequenz von acht Linienpaaren pro Bogengrad stark vertreten, so dass der in der obigen Aufnahme des Mondes vorhandene Objektkontrast von 24 Prozent zwischen Mondschatten und Himmel (siehe oben) gut wahrgenommen werden kann.

Etwas schwieriger gestaltet sich dies innerhalb des Schattenbereichs des Mondes. In der obigen Aufnah­me tauchen die stärksten Kontraste entlang einer Linie von oben nach unten auf, wo die helleren Mondebenen mit den Kratern Copernicus und Tycho durch die dunkleren Maria Imbrium und Nubium unterbrochen werden. Daraus resultiert eine Ortsfrequenz mit fünf Linienpaaren pro Bogengrad, wo die Kontrastempfindlichkeitsfunktion ebenfalls einen recht hohen Wert von 0,9 beziehungsweise 90 Prozent erreicht. Dies schwächt den auf der Mond­oberfläche vorhandenen Objektkontrast von 10 Prozent im vom Auge auf die Netzhaut übertragenen Bildkontrast nur geringfügig ab.

Aus diesen Überlegungen resultiert, dass die im aschgrauen Licht des Mondes wahrnehmba­ren Kontraste knapp 10 Prozent betragen. Diese sind zwar geringer als der Kontrast von 24 Prozent zwischen dem aschgrauen Mondlicht und dem den Mond umgebenden Himmel, sie liegen allerdings noch in einem wahrnehmbaren Bereich. Somit ist erwiesen, dass ein gesundes Auge unter idealen Beobachtungsbedingungen auch völlig ohne optische Hilfsmittel die Helligkeitsunterschiede und Strukturen im nur durch den Erdschein erhellten Schattenbereich des Mondes erkennen kann.

Es gibt jedoch zahlreiche Faktoren, die den wahrnehmbaren Kontrast deutlich herabsetzen oder die Möglichkeit der Wahrnehmung verhindern können:

Je älter ein Mensch wird, desto mehr Streulicht wird durch kleinste Verletzungen beziehungsweise Narben in der Hornhaut oder in der Linse des Auges erzeugt. Dieses Streulicht erzeugt einen mehr oder weniger gleichmäßigen Lichtschleier, der auch die dunklen Stellen auf der Netzhaut beleuchtet. Die führt in jedem Fall zu einer Herabsetzung des wahrnehmbaren Kontrastes und verhindert somit das Erkennen von schwachen Kontrasten.

Aber auch in der Natur gibt es viele begrenzende Faktoren. Hierzu gehört das natürliche Streulicht durch die Sonne in der Troposphäre, wenn diese zu dicht am Mond oder zu dicht unter dem Horizont oder gar über dem Horizont steht. In bewohnten Gegenden kommt als großer Störfaktor noch die Lichtverschmutzung hinzu. Ferner wird der Objektkontrast durch atmosphärische Störungen vermindert. Diese ergeben sich zum einen durch Dunst, Nebel oder Staub in der Atmosphäre, und zum anderen aus den langen Wegstrecken, die das Licht bei einer Beobachtung eines Himmelsobjekts durch die Troposphäre zurücklegen muss, wenn dieses sehr dicht über dem Horizont steht. Hierbei wird das den Beobachter erreichende Licht nicht nur abgeschwächt (Extinktion), sondern auch durch das Licht aller möglichen anderen Lichtquellen angereichert, das an den Luftmolekülen gestreut oder durch Mikroturbulenzen abgelenkt wurde, so dass sich die minimal vorhandene Helligkeit vergrößert und der Kontrast somit verringert. Auf der anderen Seite wird insbesondere in Horizontnähe der blaue Lichtanteil von astronomischen Objekten auf dem Lichtweg durch die Troposphäre durch die stark wellenlängenabhängige Rayleigh-Streuung seitlich abgelenkt, so dass es praktisch gar nicht mehr zum Beobachter gelangt. Dies führt zu den rötlichen Auf- und Untergängen von Sonne und Mond sowie zur Blaufärbung des Taghimmels.

Unter Umständen muss das Licht mehrere hundert Kilometer durch die Atmosphäre zurücklegen, wie in der folgenden Abbildung zu erkennen ist:

Weglängen für Lichtstrahlen in der 15 Kilometer hohen Troposphäre in Abhängigkeit von der Zenitdistanz.

Die Beobachtungsmöglichkeiten des aschgrauen Lichts werden grundsätzlich durch die folgenden, sich teilweise widerstrebenden Bedingungen verbessert:

• Die Lichtverschmutzung in der Atmosphäre ist gering.
• Das Mondalter beträgt wenige Tage vor oder nach Neumond.
• Die Sonne steht möglichst weit unter dem Horizont.
• Der Mond hat eine möglichst große Höhe über dem Horizont.
• Die Mondsichel ist möglichst klein, um möglichst wenig Streulicht zu verursachen.

Für die Beobachtung aus nördlichen geographischen Breiten gilt insbesondere:

• Der Mond hat eine möglichst große nördliche ekliptikale Breite zwischen seinem aufsteigenden und seinem absteigenden Knoten.
• Die Ekliptik steht möglichst steil auf dem Horizont. Dies ist bei den Tag-und-Nacht-Gleichen der Fall, besonders gut
  • abends im Frühjahr beim Neulicht des Mondes nach Sonnenuntergang im Westen.
  • morgens im Herbst beim Altlicht des Mondes vor Sonnenaufgang im Osten.

Weblinks

 Commons: Moon – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Kapitelnavigation - Die Himmelstafel von Tal-Qadi

Hauptteil | Exkurs „Tarxien“| Exkurs „Die Plejaden“ | Exkurs „Astronomische Bezugssysteme“ | Exkurs „Mondzyklen“ | Exkurs „Konjunktionen“ | Java-Programm zur Berechnung der ekliptikalen Koordinaten von Mond und Sonne