Diskussion:Musiklehre: Intervalle (Tonabstände)

Intervalle sind eigentlich Ordnungszahlen -- nein sind es nicht!

Hier werden mal wieder ein paar Dinge durcheinandergebracht. Intervalle sind Tonabstände und wesentlich reichhaltiger als die Ordnungszahlen. In einer Tonleiter wird gern die Bezeichnung „Quinte“ für den 5. Ton in der Tonleiter gebraucht. Mathematisch gesprochen heißt das „man identifiziert den einen mit dem anderen“. Aber das ändert nichts daran, dass es verschiedene Objekte mit unterschiedlichen Eigenschaften sind. Die Musiktheorie wird um Klassen logischer, wenn man solche polysemischen Konstrukte auseinandernimmt.

Um den Unterschied mal deutlich zu machen: Die Intervalle kleine Terz und große Terz lassen sich addieren. Man erhält eine Quinte. Wären sie Ordnungszahlen, würde aus kl. Terz + gr. Terz in C-Dur das Paar {e, es/dis} werden.

Und nein: Es wird nicht einfacher, wenn man das alles als dasselbe betrachtet.

Tobias Keinstein 11:28, 5. Mai 2008 (CEST)

hab das Ganze mal um ein paar nützliche Regeln erweitert, und in der Intervalltabelle das H zu B und B zu Bb gemacht. gruß

Große/Kleine Terzen

"

1. Eine Terz ist groß, wenn ein Halbton (z.B. E - F oder B - C) zwischen dem Intervall liegt. Beispiel E - G ist eine große Terz weil zwischen E und G noch das F liegt, und E - F ein Halbton ist.
2. Eine Terz ist klein, wenn kein Halbton dazwischen liegt"

Das ist natürlich kompletter Schwachsinn! Die Regel ist genau umgekehrt, ich habs mal umgeändert:

1. Eine Terz ist klein, wenn ein Halbton (z.B. E - F oder B - C) zwischen dem Intervall liegt. Beispiel E - G ist eine kleine Terz weil zwischen E und G noch das F liegt, und E - F ein Halbton ist.
2. Eine Terz ist groß, wenn kein Halbton dazwischen liegt

Halbtonschritte einfügen

noch nicht ganz ausgereift aber in etwa so könnte ein Fragment aussehen.

Eine Terz ist klein, wenn sie drei Halbtonschritte hat, eine Terz ist groß, wenn sie vier Halbtonschritte hat.

C-C#-D-Eb = kl. Terz = Mollterz (wenn C der Grundton ist)
C-C#-D-Eb-E = gr. Terz = Durterz (wenn C der Grundton ist)
ein Bindestrich entspricht hier einem Halbtonschritt

Eine kleine Terz besteht aus zwei kleinen Sekunden, eine große Terz besteht aus einer kleinen und einer großen Sekunde, wobei egal ist, welche der beiden Sekunden zuerst kommt. Vom Grundton eines Akkordes oder einer Tonleiter ausgehend heißt die kleine Terz auch Moll-Terz und die große Terz auch Durterz... dazu muss aber die Terz vom Grundton aus gezählt werden.

Wieviele Tasten zwischen zwei anderen stehen ist relativ. Je nachdem ob man die erste Taste mitzählt (wie man es bei den Intervallen muss), oder nicht. Halbtonschritte sind dagegen eindeutiger. In einem Lehrbuch sollte man sich nicht scheuen es überdeutlich zu erklären (zur Not mit Bildern) denn es kommt (selbst bei Profis) extrem leicht zu Verwechslungen. --mjchael 12:25, 19. Sep 2006 (CEST)

FALSCH

@Unbekannt: bitte in ganze Sätzen Antworten! So kann niemand was damit anfangen! Gruß --mjchael 19:45, 20. Mär. 2007 (CET)

Extra-Kapitel

Übermäßige und verminderte Intervalle, sowie der Tritonus verdienen einen eigenen Artikel.--mjchael 12:25, 19. Sep 2006 (CEST)

mal was Angefangen, was noch weiter gesponnen werden muss

Praktische Intervall-Lehre bei Akkorden

Egal, welchen Intervall man auch immer für einen Akkord sucht, es ist sehr empfehlenswert, dass man von den Tönen einer Dur-Tonleiter ausgeht. Eine normale Dur-Tonleiter hat nur große oder reine Intervalle, und man kann die Töne einer Dur-Tonleiter sehr einfach [[ableiten.

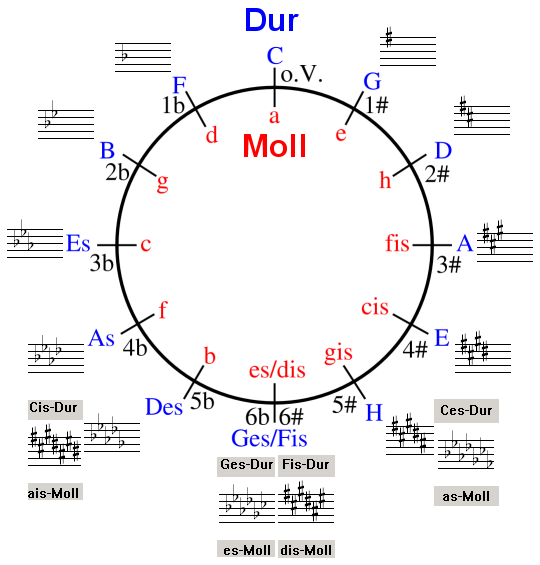
Um die Töne einer Tonleiter zu ermitteln zählt man diese nicht ab, oder lernt die Töne einer Tonleiter auswendig, sondern man lernt einmal den Quintenzirkel, und hat damit eine Schablone, von der mal alle Tonleitern ablesen kann.

Die Töne im Quintenzirkel sind immer in folgender Reihenfolge angeordnet. (Da es wesentlich einfacher ist, verwende ich hier das internationale B anstelle des deutschen H!)

• F C G D A E B

Dieses ist die Reihenfolge der Stammtöne in der C-Dur-Tonleiter. Diese Reihenfolge muss man auswendig können.

Um die Kreuztonarten zu ermitteln füge man einfach die gleiche Tonfolge rechts an...

• F C G D A E B - F C G D A E B

und füge daran noch ein #

• F C G D A E B F# C# G# D# A# E# B#

Möchte man die B-Tonarten ermitteln füge man die gleiche Tonfolge links an....

• F C G D A E B - F C G D A E B

und ergänze diese durch ein "b"

• Fb Cb Gb Db Ab Eb Bb F C G D A E B

Komplett sähe die Reihenfolge so aus

• Fb Cb Gb Db Ab Eb Bb F C G D A E B F# C# G# D# A# E# B#

Wenn man die Vorzeichen einmal nicht beachtet, so wiederholen sich die sieben Buchstaben stets in gleicher Reihenfolge, wie die Tage einer Woche. Und das ist auch schon alles, was man benötigt. Bekannter ist uns diese Reihenfolge in einem Kreis angeordnet:

Doch für alle praktischen Zwecke genügt in Zukunft ein Blatt Papier, und die Tonfolge F C G D A E B. Und mit ein wenig Übung benötigt man noch nicht einmal mehr dieses.

Möchte man die Tonfolge irgendeiner Dur-Tonleiter ermitteln, so nehme man den Linken Nachbarn und die folgenden fünf rechten Nachbarn mit hinzu.

Führen wir dieses Beispiel für den Akkord D-Dur praktisch durch.

Die D-Dur-Tonleiter besteht aus dem D, seinem Linken Nachbarn, dem G und seinen fünf rechten Nachbarn A E B F# C# also zusammen in der Reihenfolge des Quintenzirkels

• G "D" A E B F# C#

Die Intervalle werden alle vom Grundton aus ermittelt. Es sollte ein Leichtes sein, die Töne in die richtige Reihenfolge zu bringen.

• D E F# G A B C# D

Dieses mag jetzt das erste mal etwas langatmig anmuten, doch in Zukunft muss man keinen einzigen Ton mehr einzeln abzählen.

• Ein D-Dur-Akkord besteht aus den Tönen D F# A
• Dj7-Akkord besteht aus den Tönen D F# A C#
• Dsus4 besteht aus den Tönen D G A. Die Terz F# wird durch die Quarte (der vierte Ton) ersetzt.
• Dadd2 besteht aus den Tönen D E F# A. Also den Tönen von D-Dur und noch die Sekunde (der zweite) E.
• D6 sind die Töne von D-Dur mit der Sexten B also D F# A B

Drei Töne des Dur-Akkordes und die vier Tonleitereigenen Optionstöne ergeben zusammen die sieben Töne der Dur-Tonleiter.

Alle Töne, die bei einem D-Akkord von der D-Dur-Tonleiter abweichen werden extra kenntlich gemacht. Wenn sie nicht extra kenntlich gemacht werden sind es demnach große Intervalle oder reine Intervalle.

• Wenn aus der Terz F# eine Kleine Terz wird, so wird dieses mit einem "m" für Moll kenntlich gemacht. Das F# verliert dabei sein Kreuz.
• Das die kleine Septime nur mit einer 7 bezeichnet wird, und dieser Septime kein "b" vorangestellt wird, muss man einfach so hinnehmen. Jedoch wir wissen das die normale große Septime (j7) ein C# ist, brauchen wir dieser bloß das Kreuz wegzunehmen um die kleine Septime C für den D7-Akkord zu erhalten. Auch ein Dm7 hat neben der kleinen Terz F noch die kleine Septime C.

Physikalische Grundlagen

Ich finde es sinnvoll, kurz zu erklären, daß die Oktave die doppelte Frequenz bedeutet: das erklärt, warum auf der Gitarre im 12. Bund, Mitte der Saite, die Oktave als Flagolett gespielt werden kann, Bläsern wird auch manches klar, dazu der Hinweis, daß Männer und Frauen in der Regel im Oktavabstand singen und das als einstimmig empfunden wird. Ergänzend der Hinweis, daß harmonisch klingende Intervalle einfache Schwingungsverhältnisse haben, finde ich als Erklärung und Hintergrundwissen wert, hier aufgenommen werden, wenn auch nicht jeder genau wissen muß, daß die Quinte 2 zu 3 und die große Terz 4 zu 5 und der Durakkord 4 zu 5 zu 6 ist.

Wenn jetzt Zustimmung kommt erarbeite ich einen kleinen Absatz, vielleicht 10 Zeilen, vielleicht ist die Mehrheit der Meinung, daß das unnötiger Ballast ist, dann lasse ich es bleiben. Bitte schreibt eure Meinung hier.

Rüdiger Rodriguez4444 22:03, 9. Apr. 2008 (CEST)

Ganz deiner Meinung. Mir schwebt ein Artikel vor, das auf Resonanzen in einem Gebäuden (Badezimmereffekt) und dem Stimmen von Instrumenten eingeht. Beim Singen in einer Kathedrale oder in vielen Gebäuden werden bestimmte Frequenzen natürlich verstärkt. Naturhörner (Alphorn) und Saiteninstrumente sollte nachgezeichnet werden. Diese Frequenzen bilden die physikalischen Grundlage für Tonleitern (vgl. Gregorianischer Gesang).

Es spiegelt sich im Stimmen von Saiteninstrumenten wieder, und in dem Herstellen von Flöten etc. Dann auf das Stimmen von Klavieren. Es sollte bewusst nur nachgezeichnet werden, und keine historische Abhandlung sein, weil man dann ganz andere Probleme bekommt. Physikalische Phänomene sollten also mit plastischen Beispielen nachgezeichnet werden, damit man die physikalischen Grundlagen mit Inhalt füllen kann.

Gruß --mjchael 11:04, 10. Apr. 2008 (CEST)

Wenn wir über Intervalle reden, dann reden wir nicht über Ordnungsnummern, sondern über Tonabstände (vgl. Zahlenintervalle). Da ist eine reine Quinte durchaus etwas anderes ob ich eine reine oder gleichstufige Quinte habe. Bei Terzen und Septimen gibt das durchaus gravierende hörbare Effekte in der Polyphonie. Jeder Blechbläser muss das verwenden, wenn er „sauber“ blasen möchte. Er muss es zwar nicht wirklich bis ins kleinste Detail verstanden haben, weil die Intuition und das Harmonieverständnis da ne ganze Menge ausgleichen. Aber mit dem Wissen dass eine reine Terz kleiner ist als eine gleichstufige kann man manchen Dreiklang vom dissonanten Geräusch zum Wohlklang formen.

Ein anderer Aspekt ist: Hier steht Musiktheorie drüber. Dazu zählt auch den Charakter von Tonarten in den Temperierten Stimmungen (außer Gleichstufige). Das setzt einen sauberen Intervallbegriff voraus. Ansonsten könnte man den Unterschied zwischen den Wohltemperierten Stimmungen (Bach, Werckmeister, Kirnberger u.a.) und der Gleichstufigen Stimmung nicht erklären.

Tobias Keinstein 11:14, 5. Mai 2008 (CEST)

Rein, Groß, Klein (übermäßig und Vermindert)

Es gibt reine Intervalle, gleichstufige und viele andere Abarten davon. Währen das in der Harmonik leider zu selten berücksichtigt wird, ist es eine zwingende Voraussetzung wenn es um Stimmungen, Temperaturen und Tonalitäten geht. --Keinstein 11:44, 5. Mai 2008 (CEST)

Wir schreiben Lehrbücher und keine Enzyklopädie

@ Keinstein

Achtung, wir schreiben hier Lehrwerke, und keine wissenschaftlichen Abhandlungen. Es geht hier nicht um eine Darstellung des Wissens, sondern um eine Vermittlung des Wissens. Diejenigen, die das Projekt im Augenblick vorantreiben, haben sich als Zielgruppe Interessierte Laien auf Abiturniveau ausgesucht (genauer: Hobbymusiker, die in Harmonielehre weiterkommen wollen). Der Wissensstoff stellen sich auf den Schüler, nicht auf Musikstudenten und Musikwissenschaftler ein. Und da startet man am besten bei 0. Also muss man auch mit einer Stufenweisen Vermittlung und der dazu gebotenen Vereinfachung auskommen.

Deine Kritik ist zum Teil durchaus berechtigt, doch gib acht, dass du das Niveau nicht zu hoch ansetzt, so dass wirklich interessierte Hobbymusiker keinen Zugang mehr zu der Materie finden. Detailwissen gehört nicht in die einleitenden Artikel hinein. Deteilwissen sollte in weiterführende Artikel "ausgelagert" werden.

Viele Problematiken des praktischen Umgangs mit der Harmonielehre wird von Laien viel leichter verstanden, wenn man die Intervalle zuerst als Ordnungszahlen betrachtet. Bei vielem geht es einzig und allein um das Abzählen der Buchstaben (ungeachtet der Vorzeichen). Danach zählt man die Halbtonschritte um festzustellen, ob der Intervall rein, groß, klein, vermindert oder übermäßig ist. Und da sind zuerst die rein Formalen Informationen vonnöten. Besondere Klangeigenheiten der Intervalle sind in extra Artikeln auszulagern. Intervallverhältnisse und Physikalische Eigenheiten, Stimmungen und besondere Eigenheiten von Instrumenten mit einer freien Stimmung (Geige, Posaune u.ä.) oder einer reinen Stimmung (Trompete, Hörner u.ä.) oder gleichstufigen Stimmung (Piano, Gitarre) das sind alles Aspekte, die man zwar nicht vernachlässigen sollte, aber dennoch in ein Kapitel für "Fortgeschrittene" auslagert.

Ich habe deiner Kritik in soweit Rechnung getragen, dass ich die Inhalte relativiert habe. Die vereinfachte Betrachtungsweise sollte für den Laien aus pädagogischer Sicht jedoch erhalten bleiben.

Gruß --mjchael 17:18, 5. Mai 2008 (CEST)