Game of Life

Dieses Buch steht im Regal Programmierung.

Dieses Buch hat eine Druckversion.

Bildschirmaufnahme des Java-Programms **Game of Life** zur Anzeige von Conways Spiel des Lebens.

Ein einzelnes initiales f-Pentomino vernichtet den aus 22 Pulsatoren bestehenden, unterhalb stehenden Schriftzug "HELLO" in 4402 Iterationen.

Dieses Wikibook beschäftigt sich mit der softwaretechnischen Implementation von Conways Spiel des Lebens (englisch: "Game of Life") mit der Hilfe von strukturierten Java-Programmen. Zur Modellierung des räumlich diskreten dynamischen Systems wird ein zweidimensionaler zellulärer Automat implementiert.

Algorithmus für das Spiel des Lebens

In der angewandten Mathematik ist das Spiel des Lebens ein dynamisches System, das eine selbstorganisierte Entwicklung durchläuft. Hierbei entstehen aus einer gegebenen Anfangssituation aufgrund einer wohldefinierten Interaktion einzelner Systemelemente einfache und komplexe geometrische Strukturen. Jede üblicherweise quadratische Zelle auf dem Spielfeld kann entweder das Leben (englisch "live" für "lebendig") oder den Tod (englisch "dead" für "tot") repräsentieren, und das gesamte Spielfeld entwickelt sich Schritt für Schritt iterativ weiter. Für jede Zelle auf dem Spielfeld gilt:

Sie bleibt im nächsten Schritt lebendig, wenn sie genau zwei lebendige Zellen in den acht direkt benachbarten Zellen hat.
Sie bleibt oder wird im nächsten Schritt lebendig, wenn sie genau drei lebendige Zellen in den acht direkt benachbarten Zellen hat.

Das Spielfeld kann am Rand begrenzt sein, oder sich an der jeweils gegenüberliegenden Seite des Spielfelds fortsetzen, was auch als torodiale Struktur bezeichnet wird.

Bei der schrittweisen Entwicklung können statische, mit einer bestimmten Anzahl von Mustern oszillierende oder sich über das Spielfeld bewegende Strukturen entstehen. Es ist möglich, dass auf dem gesamten Spielfeld zu einem bestimmten Zeitpunkt sich keine Zellen mehr über das Spielfeld bewegen, keine Strukturen mehr oszillieren oder sogar alle Zellen statisch sind.

Der Algorithmus für das Spiel aus dem Jahr 1970 geht auf den britischen Mathematiker John Horton Conway (1937 bis 2020) zurück.

→ Siehe auch deutschsprachiger Wikipedia-Artikel Conways Spiel des Lebens.

→ Siehe auch englischsprachiger Wikipedia-Artikel Conway's Game of Life.

Beispiele für Figuren im Spiel des Lebens
Die statische Figur "Honey farm" ("Honigfarm") aus vier statischen Figuren "Bee hive" ("Bienenkorb") mit insgesamt 13 mal 13 Zellen.
Die oszillierende Figur "Clover" in Form eines Kleeblatts mit 15 mal 15 aktiven Zellen aus drei sich wiederholenden Mustern.
Die von links oben nach rechts unten gleitende Figur "Glider" mit 3 mal 3 aktiven zusammenhängenden Zellen.

Programmbestandteile

Das hier vorgestellte Java-Programm implementiert ein rechteckiges Spielfeld mit wählbarer Breite und Höhe. Hierzu werden für die Modellierung, die graphische Anzeige und die Initialisierung eines Spielfelds die drei Java-Klassen GameOfLifeModel, GameOfLifeFrame und GameOfLife verwendet, die im Folgenden beschrieben werden.

GameOfLifeModel

Die Java-Klasse GameOfLifeModel dient der Implementierung eines Modells für die Umsetzung des Spiels des Lebens in einer rechteckigen Fläche.

Die Spielfläche in einem rechteckigen Spielfeld aus $x$ mal $y$ Zellen kann aus zwei verschiedenen Elementen zusammengesetzt werden:

Tote Zelle (GameOfLifeModel.DEAD)
Lebende Zelle (GameOfLifeModel.LIVE)

Die entsprechenden öffentlichen Konstanten für diese Aufzählung sind in der Java-Klasse "GameOfLifeModel" definiert. Ferner gibt es die beiden Konstanten ALWAYS_DEAD und TORODIAL, mit denen das Verhalten der Zellen an den Rändern des Spielfelds gesteuert werden kann:

	// Class constants for state of fields
	public final static boolean DEAD = false;
	public final static boolean LIVE = true;

	// Class constants for mode of the borders
	public final static boolean ALWAYS_DEAD = false;
	public final static boolean TORODIAL = true;

Das Modell verwendet zwei zweidimensionalen Datenfelder (Arrays), um aus einem bestehenden Spielfeld, das in der Instanzvariablen GameOfLifeModel.currentBoard gespeichert ist, das nächstes Spielfeld zu berechnen, das in der Instanzvariable GameOfLifeModel.nextBoard zwischengespeichert wird. Jede Zelle des Spielfelds enthält einen booleschen Wert (Datentyps "boolean"), in dem die beiden oben genannten Werte gespeichert werden können. Mit dem Konstruktor GameOfLifeModel (int width, int height, boolean borderMode) der Klasse werden die Breite width und die Höhe height des rechteckigen Spielfelds sowie das Verhalten borderMode an den Spielfeldrändern festgelegt, und die beiden zweidimensionalen Datenfelder GameOfLifeModel.currentBoard und GameOfLifeModel.nextBoard werden erzeugt:

	/**
	* Constructor for the initialisation of game board instances of the class GameOfLifeModel
	* @param width: for the horizontal size
	* @param height: for the vertical size
	* @param borderMode: for the mode of the border, either ALWAYS_DEAD or TORODIAL
	*/
	public GameOfLifeModel (int width, int height, boolean borderMode)
	{
		this.sizeX = width;
		this.sizeY = height;
		this.borderMode = borderMode;
		this.currentBoard = new boolean [width] [height];
		this.nextBoard    = new boolean [width] [height];
	}

Für das hier implementierte Modell gelten die oben angegebenen Regeln. Eine Iteration wird mit dem Aufruf der Methode computeNextBoard () durchgeführt:

	/**
	 * Computing next board
	 */
	public void computeNextBoard ()
	{
		for (int y = 0; y < sizeY; y++)
		{
			for (int x = 0; x < sizeX; x++)
			{
				long numberOfLiveNeighbours = countLiveNeighbours (x, y);
				if (numberOfLiveNeighbours == 2)
				{
					nextBoard [x] [y] = currentBoard [x] [y];
				}
				else if (numberOfLiveNeighbours == 3)
				{
					nextBoard [x] [y] = LIVE;
				}
				else
				{
					nextBoard [x] [y] = DEAD;
				}
			}
		}
		copyNextToCurrentField ();
	}

Hierbei wird mit der Methode long countLiveNeighbours (int x, int y) für jede Zelle (x, y) des Spielfelds untersucht, wie viele der benachbarten acht Zellen lebendig sind.

	/**
	 * Counting all live neighbours of cell (x, y)
	 * @param x: horizontal position
	 * @param y: vertical position
	 * @return number of live neighbours
	 */
	private long countLiveNeighbours (int x, int y)
	{
		long numberOfLiveNeighbours = 0;
		if (upperLeftNeighbourIsLive (x, y))  {numberOfLiveNeighbours++;}
		if (upperNeighbourIsLive (x, y))      {numberOfLiveNeighbours++;}
		if (upperRightNeighbourIsLive (x, y)) {numberOfLiveNeighbours++;}
		if (leftNeighbourIsLive (x, y))       {numberOfLiveNeighbours++;}
		if (rightNeighbourIsLive (x, y))      {numberOfLiveNeighbours++;}
		if (lowerLeftNeighbourIsLive (x, y))  {numberOfLiveNeighbours++;}
		if (lowerNeighbourIsLive (x, y))      {numberOfLiveNeighbours++;}
		if (lowerRightNeighbourIsLive (x, y)) {numberOfLiveNeighbours++;}
		return numberOfLiveNeighbours;
	}

Mit den beiden gebundenen öffentlichen Methoden int getWidth () und int getHeight () können die Abmessungen des Spielfelds abgerufen werden. Durch Aufruf der öffentlichen Methode boolean model.getCellState (x, y) wird der Zustand der Zelle an der Stelle (x, y) zurückgegeben. Mit der öffentlichen Methode setCellState (int x, int y, boolean state) kann der Status der Zelle (x, y) auf DEAD oder LIVE gesetzt werden.

Mit dem folgenden Java-Programm mit der Java-Klasse GameOfLifeModel können Modelle des Spiels des Lebens erzeugt und verwaltet werden:

→ Java-Programm "GameOfLifeModel"

GameOfLifeFrame

Die Java-Klasse GameOfLifeFrame realisiert als Erweiterung der Java-Standardklasse javax.swing.JFrame (Basisklasse ist java.awt.Component, und der Name des Software-Pakets "awt" steht für "advanced windows toolkit", was ungefähr als "fortgeschrittener Fenster-Werkzeugsatz" übersetzt werden kann) eine iterativ aktualisierte graphische Ausgabe von Inhalten der Klasse GameOfLifeModel:

java.awt.Component
- java.awt.Container
  - java.awt.Window
    - java.awt.Frame
      - javax.swing.JFrame
        GameOfLifeFrame

Für die graphische Ausgabe einer Instanz model der Klasse GameOfLifeModel werden Instanzen der Java-Klassen java.awt.image.BufferedImage und java.awt.image.WritableRaster verwendet. Eine Instanz der Klasse GameOfLifeFrame wird mit der überschriebenen parameterlosen Java-Standardmethode init () initialisiert und mit der überschriebenen, öffentlichen und typengebundenen Java-Standardmethode paint () ausgegeben. Die Methode paint () benötigt dafür als Parameter eine Instanz der Java-Klasse java.awt.Graphics.

Zur Synchronisation der graphischen Ausgabe wird eine Instanz der Java-Standardklasse java.awt.event.ActionListener implementiert. Hierbei handelt es sich um ein Java-Interface, das Ereignisse der Klasse java.awt.event.ActionEvent empfängt: Ereignisse zur aktualisierten graphischen Ausgabe werden mit Hilfe einer Instanz der Java-Klasse javax.swing.Timer ausgelöst. Dieser Zeitgeber wird durch den Aufruf seines Konstruktors javax.swing.Timer (50, this) mit einem Verzögerungsparameter (hier 50 Millisekunden) als ActionListener erstellt, und die Instanz der Klasse javax.swing.JFrame wird von diesem Zeitgeber durch den Aufruf seiner Methode addActionListener () automatisch intern registriert. Der Verzögerungsparameter wird verwendet, um die Verzögerung jeder Iteration in Millisekunden festlegen zu können.

public final class GameOfLifeFrame extends javax.swing.JFrame implements java.awt.event.ActionListener
{
	// Class constants
	public static final boolean Save = true;
	public static final boolean DontSave = false;

	// Instance variables
	private GameOfLifeModel model;
	private java.awt.image.BufferedImage bufferedImage;
	private java.awt.image.WritableRaster imageRaster;
	private javax.swing.Timer timer = new javax.swing.Timer (50, this); // for the delay between two subsequent JFrames
}

Der Konstruktor GameOfLifeFrame (int x, int y, boolean mode, long count, boolean saveBoard) zur Initialisierung der graphischen Ausgabe des Spiels ist folgendermaßen gestaltet, um ein Spielfeld (englisch: "board") mit der Breite x und der Höhe y für count Iterationen zu erzeugen:

	/**
	 * Constructor for the initialisation of instances of the class GameOfLifeFrame
	 * @param width: horizontal board size in pixel
	 * @param height: vertical board size in pixel
	 * @param mode: border handling, either GameOfLifeModel.ALWAYS_DEAD or GameOfLifeModel.TORODIAL
	 * @param count: number of steps for the iterations
	 * @param saveBoard: saveBoards to PNG file, either Save or DontSave
	 */
	public GameOfLifeFrame (int width, int height, boolean mode, long count, boolean saveBoard)
	{
		super (title);
		this.model = new GameOfLifeModel (width, height, mode);
		this.sizeX = width;
		this.sizeY = height;
		this.numberOfIterations = count;
		this.save = saveBoard;

		// Rahmengroesse, Hintergrund und das Layout werden gesetzt
		this.setSize (this.sizeX + 2 * offset, this.sizeY + 2 * offset + offsetTop);
		this.setBackground (java.awt.Color.WHITE);
		this.bufferedImage = new java.awt.image.BufferedImage (this.sizeX, this.sizeY, java.awt.image.BufferedImage.TYPE_INT_RGB);
		this.imageRaster = bufferedImage.getWritableTile (0, 0);
		this.setDefaultCloseOperation (javax.swing.WindowConstants.EXIT_ON_CLOSE);
	}

Die Simulation wird mit dem Aufruf der Methode init () gestartet. Bevor innerhalb der Methode init () die graphische Ausgabe mit dem Aufruf der Methode paint () zum ersten Mal erfolgt, wird der bereits registrierte javax.swing.Timer durch den Aufruf seiner Methode timer.start () gestartet:

	/*
	 *  Method for the initialisation of an instance of GameOfLifeFrame
	 */
	public void init ()
	{
		java.awt.Graphics2D graphics2D = bufferedImage.createGraphics ();
		this.paint (graphics2D);
		this.setVisible (true);
		this.setAlwaysOnTop (true);
		this.timer.start ();
	}

Sobald der Zeitgeber mit der gebundenen Methode start () aus der Klasse javax.swing.Timer im Konstruktor der Klasse GameOfLifeFrame gestartet wurde, wartet dieser jeweils für die vorgegebene Zeit in Millisekunden, bevor ein Ereignis der Klasse java.awt.event.ActionEvent an den registrierten java.awt.event.ActionListener auslöst werden kann.

Wenn das Ereignis ausgelöst wurde, wird die Methode actionPerformed (java.awt.event.ActionEvent event) des Objekts mit einem Parameter event der Klasse java.awt.event.ActionEvent aufgerufen, die schließlich wiederum die Java-Standardmethode java.awt.Component.repaint () aufruft, die intern dann wiederum die Standard-Methode paint () aufruft. Am Ende des Spiels wird der Zeitgeber timer durch den Aufruf der gebundenen Methode timer.stop () aus der Klasse javax.swing.Timer angehalten.

Die aus der Basisklasse java.awt.event.ActionListener überschriebene Standardmethode actionPerformed (java.awt.event.ActionEvent event) für die synchronisierte Aktualisierung einer Instanz der Klasse GameOfLifeFrame sieht folgendermaßen aus:

	/**
	 * Overwritten standard method actionPerformed for the synchronised update of an instance GameOfLifeFrame
	 */
	public void actionPerformed (java.awt.event.ActionEvent event)
	{
		java.lang.String currentTitel = title + " / step " + currentStepNumber;
		if (currentStepNumber < numberOfIterations)
		{
			currentStepNumber++;
			model.computeNextField ();
			if (this.save)
			{
				this.saveFile (bufferedImage);
			}
			repaint ();
		}
		else
		{
			currentTitel = currentTitel + " / game over";
			timer.stop ();
		}
		setTitle (currentTitel);
	}

Mit dem Aufruf der Methode java.awt.Toolkit.getDefaultToolkit ().sync () am Ende der Standardmethode paint (java.awt.Graphics graphics) zur graphischen Darstellung der Instanz graphics wird sichergestellt, dass die graphische Anzeige vollständig aktualisiert ist, bevor durch den Zeitgeber ein neues Ereignis (java.awt.event.ActionEvent) ausgelöst wird:

	/**
	 * Standard method paint for painting a rectangular field of the Game of Life
	 * @param graphics: instance of java.awt.Graphics
	 */
	public void paint (java.awt.Graphics graphics)
	{
		for (int y = 0; y < sizeY; y++)
		{
			for (int x = 0; x < sizeX; x++)
			{
				boolean cellState = model.getCellState (x, y);
				if (cellState == GameOfLifeModel.DEAD)
				{
					imageRaster.setPixel (x, y, DeadColour);
				}
				else
				{
					imageRaster.setPixel (x, y, LiveColour);
				}
			}
		}
		graphics.drawImage (bufferedImage, offset, offset + offsetTop, null);
		java.awt.Toolkit.getDefaultToolkit ().sync (); // This method call ensures that the display is up-to-date
	}

Mit dem folgenden Java-Programm mit der Java-Klasse GameOfLifeFrame kann die Bildschirmanzeige des Spiels des Lebens realisiert werden:

→ Java-Programm "GameOfLifeFrame"

Aufruf des Programms

Mit dem Aufruf des beispielhaften öffentlichen Hauptprogramms main (java.lang.String [] arguments) in der Klasse GameOfLife werden 1000 Schritte für ein Spielfeld mit 800 Feldern in der Breite und 600 Feldern in der Höhe berechnet und graphisch dargestellt. Der Aufruf des Konstruktors GameOfLifeFrame (width, height, GameOfLifeModel.TORODIAL, numberOfIterations, GameOfLifeFrame.DontSave) erzeugt eine entsprechende Instanz frame der Klasse GameOfLifeFrame, wobei dieser automatisch den Konstruktor GameOfLifeModel (width, height, GameOfLifeModel.TORODIAL) der Java-Klasse GameOfLifeModel aufruft und somit eine Instanz model dieser Klasse erzeugt. Mit dem Unterprogramm init (GameOfLifeModel model) kann diese Instanz initialisiert werden.

Mit dem Aufruf der Methode model.setCellState (x, y, GameOfLifeModel.LIVE) wird der boolesche Zustand status der Zelle an der Stelle (x, y) des Spielfelds auf "lebendig" gesetzt. Die beiden möglichen Zustände sind in den Konstanten DEAD und LIVE der Klasse GameOfLifeModel definiert.

In dem Java-Programm mit der Java-Klasse PseudoRandom sind die Unterprogramme (Methoden) enthalten, mit denen in der Klasse GameOfLife die entsprechenden Pseudozufallszahlen erzeugt werden:

→ Siehe Java-Programm "PseudoRandom"

Von der Methode double nextProbability () wird eine pseudozufällige Gleitkommazahl zwischen Null und Eins zurückgegeben, mit der in diesem Beispiel hier gesteuert wird, welche Zellen des Spiels zu Beginn pseudozufällig als lebendig gesetzt werden.

public class GameOfLife
{
	// class variables for the size of the game board
	private static int width = 800;
	private static int height = 600;

	// class variable for the pseudorandom numbers
	private static long currentRandomnumber = 1;

	// class constants for computing the next pseudorandom number
	final private static long m = 9095665192937L; // large prime number
	final private static long a = 3 * 7 * 11 * 13 * 17 * 19; // product of six small prime numbers, value = 969969

	// set currentRandomnumber to startwert
	public static void setStartValue (long startwert)
	{
		currentRandomnumber = startwert;
	}

	// set currentRandomnumber to system time in milliseconds
	public static void setStartValueToSystemTime ()
	{
		setStartValue (java.lang.System.currentTimeMillis ());
	}

	// compute next pseudorandom integer number in the interval [1..m-1] (inclusive)
	private static void nextRandomnumber ()
	{
		currentRandomnumber = a * currentRandomnumber % m;
	}

	// compute next pseudorandom integer number in the interval [0..1] (exclusive 0 und 1)
	public static double nextProbability ()
	{
		nextRandomnumber ();
		double probability = (double) currentRandomnumber / m;
		return probability;
	}

	// compute initial pseudorandom pattern for Game of Life board
	private static void setRandomPattern (GameOfLifeModel model, double thresholdProbabilty)
	{
		for (int y = height / 16; y < 15 * height / 16; y++)
		{
			for (int x = width / 16; x < 15 * width / 16; x++)
			{
				double probabilty = nextProbability ();
				if (probabilty <= thresholdProbabilty)
				{
					model.setCellState (x, y, GameOfLifeModel.LIVE);
				}
			}
		}
	}

	// initialise Game of Life board
	private static void init (GameOfLifeModel model)
	{
		setStartValueToSystemTime ();
		setRandomPattern (model, 0.25); // a maximum of 25 percent of all cells will be set alive
	}

	// main programm to be called by runtime system
	public static void main (java.lang.String [] arguments)
	{
		long numberOfIterations = 1000;
		GameOfLifeFrame frame = new GameOfLifeFrame (width, height, GameOfLifeModel.TORODIAL, numberOfIterations, GameOfLifeFrame.DontSave);
		GameOfLifeModel model = frame.getModel ();
		init (model);
		frame.init ();
	}
}

Unterprogramme für Strukturen

Mit den folgenden beispielhaften Methoden können im leeren Spielfeld interessante Strukturen gesetzt werden.

Gleiter

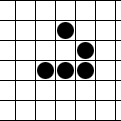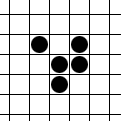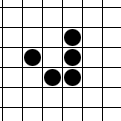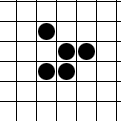
Die in diesem Beispiel von links oben nach rechts unten gleitende Figur "Gleiter" (Englisch: "Glider") besteht aus drei mal drei aktiven zusammenhängenden Zellen, von denen jeweils fünf lebendig sind, die sich wiederum in einem Zyklen mit vier aufeinander folgenden Zuständen wiederholen.

Wegen der Asymmetrie des Gleiters kann dieser auch in drei jeweils um einen rechten Winkel gedrehten Richtungen gestartet werden.

private static void setGlider (GameOfLifeModel model, int x, int y)
{
	model.setCellState (x,     y - 1, GameOfLifeModel.LIVE);
	model.setCellState (x + 1, y,     GameOfLifeModel.LIVE);
	model.setCellState (x - 1, y + 1, GameOfLifeModel.LIVE);
	model.setCellState (x,     y + 1, GameOfLifeModel.LIVE);
	model.setCellState (x + 1, y + 1, GameOfLifeModel.LIVE);
}

f-Pentomino

Die Figur "f-Pentomino" erreicht erst nach 1102 Generationen einen oszillierenden Zustand und entlässt bis dahin sechs Gleiter, drei nach rechts unten, einen nach rechts oben und zwei nach links oben.

Wegen der Asymmetrie der initialen Struktur kann ein f-Pentomino auch in drei jeweils um einen rechten Winkel gedrehten Richtungen gestartet werden.

private static void setFPentomino (GameOfLifeModel model, int x, int y)
{
	model.setCellState (x,     y,     GameOfLifeModel.LIVE);
	model.setCellState (x + 1, y - 1, GameOfLifeModel.LIVE);
	model.setCellState (x + 1, y,     GameOfLifeModel.LIVE);
	model.setCellState (x + 1, y + 1, GameOfLifeModel.LIVE);
	model.setCellState (x + 2, y + 1, GameOfLifeModel.LIVE);
}

Pulsator

Der Zyklus von einem Pulsator besteht aus fünfzehn Mustern, die optisch eine insbesondere in horizontaler Richtung pulsierende Struktur ergeben. Ein Pulsator kann auch im rechten Winkel gedreht werden, um eine pulsierende Struktur in vertikaler Richtung zu erzeugen.

private static void setPulsator (GameOfLifeModel model, int x, int y)
{
	model.setCellState (x+2, y-1, GameOfLifeModel.LIVE);
	model.setCellState (x+7, y-1, GameOfLifeModel.LIVE);

	model.setCellState (x  , y, GameOfLifeModel.LIVE);
	model.setCellState (x+1, y, GameOfLifeModel.LIVE);
	model.setCellState (x+3, y, GameOfLifeModel.LIVE);
	model.setCellState (x+4, y, GameOfLifeModel.LIVE);
	model.setCellState (x+5, y, GameOfLifeModel.LIVE);
	model.setCellState (x+6, y, GameOfLifeModel.LIVE);
	model.setCellState (x+8, y, GameOfLifeModel.LIVE);
	model.setCellState (x+9, y, GameOfLifeModel.LIVE);

	model.setCellState (x+2, y+1, GameOfLifeModel.LIVE);
	model.setCellState (x+7, y+1, GameOfLifeModel.LIVE);
}

Oktagon

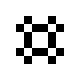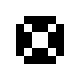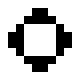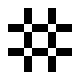
Der Zyklus von einem Oktagon besteht aus fünf Mustern, die optisch eine leicht pulsierende vierzählige Struktur ergeben.

private static void setOctagon (GameOfLifeModel model, int x, int y)
{
	model.setCellState (x+1, y  , GameOfLifeModel.LIVE);
	model.setCellState (x+4, y  , GameOfLifeModel.LIVE);
	model.setCellState (x  , y+1, GameOfLifeModel.LIVE);
	model.setCellState (x+2, y+1, GameOfLifeModel.LIVE);
	model.setCellState (x+3, y+1, GameOfLifeModel.LIVE);
	model.setCellState (x+5, y+1, GameOfLifeModel.LIVE);
	model.setCellState (x+1, y+2, GameOfLifeModel.LIVE);
	model.setCellState (x+4, y+2, GameOfLifeModel.LIVE);
	model.setCellState (x+1, y+3, GameOfLifeModel.LIVE);
	model.setCellState (x+4, y+3, GameOfLifeModel.LIVE);
	model.setCellState (x  , y+4, GameOfLifeModel.LIVE);
	model.setCellState (x+2, y+4, GameOfLifeModel.LIVE);
	model.setCellState (x+3, y+4, GameOfLifeModel.LIVE);
	model.setCellState (x+5, y+4, GameOfLifeModel.LIVE);
	model.setCellState (x+1, y+5, GameOfLifeModel.LIVE);
	model.setCellState (x+4, y+5, GameOfLifeModel.LIVE);
}

Nachwort

Die hier angegebenen strukturierten Programmbeispiele können ohne große Umstände in jede andere strukturierte Programmiersprache übertragen werden. Durch die Modifikation und Ergänzung der angegebenen Algorithmen können beliebig anders gestaltete Anfangssituationen gestaltet werden.

Es wäre erfreulich, wenn dieses Wikibook zu einem besseren und tieferen Verständnis der strukturierten Programmierung und als Einstieg in die Technik der Programmierung von Iterationen mit zellulären Automaten beitragen kann.

Siehe auch

Zusammenfassung des Projekts

„Game of Life“ ist nach Einschätzung seiner Autoren zu 100 % fertig

Zielgruppe: Informatiker, Mathematiker
Lernziele: Iteration eines zweidimensionalen zellulären Automaten mit einem Java-Programm.
Buchpatenschaft/Ansprechperson: Benutzer:Bautsch
Sind Co-Autoren gegenwärtig erwünscht? Ja, sehr gerne. Korrekturen von offensichtlichen Fehlern direkt im Text; Inhaltliches bitte per Diskussion.
Richtlinien für Co-Autoren: Wikimedia-like.