Himmelsgesetze der Bewegung/ Kontinuitätsgleichung

Aggregatzustände

Die drei klassischen Aggregatzustände

(aus wiki leicht geändert)

Als Aggregatzustände werden die unterschiedlichen Zustände eines Stoffes bezeichnet, die sich durch bloße Änderungen von Temperatur oder Druck ineinander umwandeln können. Es gibt die drei klassischen Aggregatzustände fest, flüssig und gasförmig sowie in der Physik weitere nicht klassische Zustände wie z. B. das Plasma.

Die drei klassischen Aggregatzustände kann man wie in Folgendem unterscheiden:

fest: In diesem Zustand behält ein Stoff meist sowohl Form als auch Volumen bei.
flüssig: Hier wird das Volumen beibehalten, aber die Form passt sich dem umgebenden Raum (z.B. dem Behälter, der Flasche usw.) an. Das Volumen beibehalten bedeutet, dass man die Flüssigkeit (in idealem Fall) nicht zusammendrücken kann.
gasförmig: Hier werden sowohl Form als auch Volumen nicht beibehalten. Ein Gas kann man zusammendrücken (wie in einer Pumpe) und es füllt den zur Verfügung stehenden Raum vollständig aus.

Für flüssige Stoffe und Gase gibt es den zusammenfassenden Begriff Fluide.

Für feste Stoffe und flüssige Stoffe gibt es den zusammenfassenden Begriff kondensierte Materie.

Bei Feststoffen unterscheidet man auch nach anderen Merkmalen:

kristallin: Ein Feststoff, dessen Bausteine, die Kristalle, eine geordnete Struktur aufweisen.
amorph: Ein Feststoff, dessen Bausteine sich in einer zufälligen Art miteinander verbinden.

Teilchenmodell der Zustände

Eine Grundtheorie der Physik ist, dass alle Körper aus Teilchen (Atome, Moleküle) bestehen. In vielen Theorien der klassischen Physik stellt man sich diese Teilchen als kleine Kügelchen vor. Das Teilchenmodell der Aggregatzustände kann man in die folgende Tabelle zusammenfassen:

	Abstand zwischen Teilchen	Bewegung der Teilchen	Kräfte zwischen Teilchen
Feste Körper	klein	Schwingungen um eine fixe Stelle	groß
Flüssigkeiten	klein	freie aber durch Stoße stark beschränkte Bewegung	groß, eher kleiner als bei festen Körpern
Gase	groß	freie und durch Stoße wenig beschränkte Bewegung	kaum vorhanden, nur während der Stöße

Kontinuitätsgesetz

Definition

"Das Kontinuitätsgesetz besagt, dass der Massenstrom eines Fluids (Flüssigkeit oder Gas) in einem Rohr unabhängig davon ist, wo er gemessen wird."(wiki). Das bedeutet, dass unter bestimmten Bedingungen (z.B. wenn man das Fluid nicht zusammendrücken kann: Inkompressibilität oder wenn die Strömung nicht von der Zeit abhängt: Stationärer Zustand) so viel Masse des Fluids in einer Seite des Rohrs hineinkommen wird, wie die Masse, die aus der anderen Seite herauskommen wird. Durch die beide Seiten fließt die gleiche Menge Fluid, also der Massenstrom ist auf beiden Seiten (und bei jedem Querschnitt) gleich.

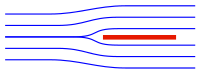
Stromlinien

Stromlinien...
...bei einem LKW
...bei einem Zylinder
...bei einer senkrechte Platte
...bei einer waagerechte Platte
...bei verschiedenen Formen
...bei einem Automodell

Stromlinien sind geometrische Hilfsmittel zur Veranschaulichung der Bewegung eines Fluiden. Die Stromlinien sind in der Richtung der Bewegung dargestellt. Sie sind dichter nebeneinander dargestellt da, wo die Geschwindigkeit des Fluiden größer ist.Sie sind hilfreich bei der Untersuchung aerodynamischer Eigenschaften.

Stromarten

Laminare Strömung Die laminare Strömung ist eine Bewegung von Fluiden, bei der (noch) keine sichtbaren Turbulenzen (Verwirbelungen/Querströmungen) auftreten: Das Fluid strömt in Schichten, die sich nicht miteinander vermischen. In diesem Fall handelt es sich (bei konstanter Strömungsgeschwindigkeit) meistens um eine stationäre Strömung. Ein Beispiel sieht man im Bild mit der waagerechten Platte. Das Gegenteil einer laminaren Strömung ist die sogenannte: turbulente Strömung Die turbulente Strömung ist die Bewegung von Fluiden, bei der Verwirbelungen über einen weiten Bereich von Größenskalen auftreten. Ein extremes Beispiel sieht man im Bild mit der senkrechten Platte. Ideale Strömung Bei einer idealen Strömung wird angenommen, dass es keine Reibung gibt und daher kein Verlust von mechanischen (kinetischen und potenziellen) Energie oder Wärme.	Turbulenz (Verwirbelung): dynamisches Bild	Turbulenz (Verwirbelung): statisches Bild

Inkompressible Fluide

(aus wiki, stark geändert)

In Folgendem wird eine konstante Dichte angenommen. Formen wir ihre Formel auf die Masse um ( $m=\rho \cdot V$ ), stellen wir fest, dass gleiche Masse gleiches Volumen bedeutet. Nach dem Kontinuitätsgesetz sollte daher auch so viel Volumen austreten, wie das eintretende Volumen ist.

In nebenstehender Abbildung sind die beiden Volumina grau markiert. Das eintretende Volumen ist im Bild links dargestellt. Mit der Geschwindigkeit v₁ tritt in einer Zeit Δt ins Rohr der Teil Δx₁ ein, also ist das eintretende Volumen:

$V_{1}=A_{1}\cdot \Delta x_{1}$

Das austretende Volumen ist im Bild rechts dargestellt. Mit der Geschwindigkeit v₂ tritt in einer Zeit Δt aus dem Rohr der Teil Δx₂ aus, also ist das austretende Volumen:

$V_{2}=A_{2}\cdot \Delta x_{2}$

Wegen $V_{1}=V_{2}$ ist im engeren Teil des Rohres die Verschiebung $\Delta x_{2}$ um denselben Faktor größer als $\Delta x_{1}$ , um den der Querschnitt $A_{1}$ größer ist als $A_{2}$ :

${\begin{aligned}V_{1}&=V_{2}\\A_{1}\cdot \Delta x_{1}&=A_{2}\cdot \Delta x_{2}\\{\frac {A_{1}}{A_{2}}}&={\frac {\Delta x_{2}}{\Delta x_{1}}}\qquad (1)\\\end{aligned}}$

Gleiches gilt für die (über den Querschnitt gemittelten) Strömungsgeschwindigkeiten $\mathrm {v} ={\frac {\Delta x}{\Delta t}}$ :

${\frac {A_{1}}{A_{2}}}={\frac {v_{2}}{v_{1}}}\qquad (2)$

Diesen Zusammenhang fand Giovanni Battista Venturi.

Kompressible Fluide

(aus wiki, leicht geändert)

Nach dem Kontinuitätsgesetz soll für kompressible Fluide (also Fluide, die man zusammendrücken kann) bzw. Fluide, die ihre Dichte ändern können, bei einer stationäre Strömung gelten:

$Q={\frac {\Delta m}{\Delta t}}=v\cdot A\cdot \rho ={\text{konstant}}$

wobei Q der konstante Massenstrom ist.

Also:

$v_{1}\cdot A_{1}\cdot \rho _{1}=v_{2}\cdot A_{2}\cdot \rho _{2}$

\rho _{1,2}

= Dichte im Rohr 1 bzw. 2

Somit gilt bei einer stationäre Strömung: Die Masse, die an einer Seite hineingeht, muss an der anderen Seite wieder herauskommen.

Die Dichte des Fluids kann sich zum Beispiel ändern, wenn sich die Temperatur des Fluids zwischen Anfang und Ende des Rohres ändert. Wenn sich die Dichte vermindert, muss in der gleichen Zeit ein größeres Volumen herauskommen.

Verkehr

(aus wiki geändert)

Im Gegensatz zum ersten Anschein verhalten sich auch Autos im Verkehrsstau bei einer Fahrbahnverengung entsprechend dem Kontinuitätsgesetz. Dabei muss der Abstand der Autos als Dichte mit betrachtet werden. Bei großem Querschnitt ist die Dichte gering, die Geschwindigkeit hoch und der Verkehr fließt frei. Im Stau vor der Einengung ist die Dichte hoch und die Geschwindigkeit gering. In der Einengung ist der Querschnitt klein, die Geschwindigkeit und die Dichte mittelgroß, und der Fahrzeugdurchsatz in allen Fällen gleich, sofern kein Auto die Straße verlässt oder hinzukommt.

Blutkreislauf

Obwohl der Blutkreislauf überhaupt kein stationäres System ist, kann man mit Hilfe dieses Kapitels verstehen, dass seiner Aufbau wichtig für seine Funktion ist. Die Summe der Querschnitte der Kapillare ist viel größer als der Querschnitt der Arterien und daher ist die Geschwindigkeit des Blutes in den Kapillaren sehr gering, was den Austausch der Stoffe erheblich erleichtert.

Druck in Strömungen

Gleichbleibende potenzielle Energie

Was passiert mit dem Druck eines strömenden Fluides in einem Rohr mit unterschiedlichen Querschnittflächen?

Um diese Frage zu beantworten, fangen wir mit der Definition der Arbeit ( $W=F\cdot s$ ; die Kraft wird hier parallel zur Verschiebung angenommen) und des Druckes ( $p={\frac {F}{A}}$ ) an. Formen wir letztere Formel auf die Kraft um ( ${F}=p\cdot {A}$ ) und setzen wir diesen Ausdruck für die Kraft in die erste Formel ein:

$W=F\cdot \Delta s=p\cdot {A}\cdot \Delta s=p\cdot \Delta V$

V ist hier das ein- bzw. ausgetretene Volumen.

Diese ist die notwendige Arbeit, um das Fluid ins Rohr zu schieben.

Eine ideale Strömung wird angenommen (daher bleibt die Gesamtenergie erhalten) und auch, dass die potenzielle Energie des Fluides gleich bleibt (das Rohr führt nicht nach oben oder nach unten). Daher kann sich die Arbeit nur in Bewegungsenergie umwandeln. Die Summe der Arbeit und der Bewegungsenergie auf der linken Seite L des Rohrs muss daher gleich der Summe der Arbeit und der Bewegungsenergie auf der rechten Seite R des Rohrs sein, dabei ist der Massenstrom und das ein- bzw. ausgetretene Volumen auf beiden Seiten gleich):

$p_{L}\cdot \Delta V_{L}+{1 \over 2}\Delta m_{L}\cdot v_{L}^{2}=p_{R}\cdot \Delta V_{R}+{1 \over 2}\Delta m_{R}\cdot v_{R}^{2}\qquad (1)$

Laut Annahme ist ΔV_L=ΔV_R(=ΔV) und Δm_L=Δm_R(=Δm). Dividieren wir beide Seiten durch ΔV:

$p_{L}\cdot +{1 \over 2}{\frac {\Delta m}{\Delta V}}\cdot v_{L}^{2}=p_{R}\cdot +{1 \over 2}{\frac {\Delta m}{\Delta V}}\cdot v_{R}^{2}$

${\frac {\Delta m}{\Delta V}}$ ist nichts anderes als die Dichte des Fluides, also können wir schreiben:

$p_{L}\cdot +{1 \over 2}\rho \cdot v_{L}^{2}=p_{R}\cdot +{1 \over 2}\rho \cdot v_{R}^{2}=p_{ges}$

Der Gesamtdruck p_ges besteht also aus zwei Teilen, einen Druck in der Richtung der Bewegung und einen, der auf die Wände der Rohrs ausgeübt wird. Da, wo die Geschwindigkeit größer ist, ist der auf die Wand ausgeübte Druck doch kleiner, wie man auch im Bild links sehen kann!

Bei Änderung der potenziellen Energie

In diesem Beispiel führt das Rohr nach oben, also ein Teil der Energie unten wird oben zur potenzielle Energie umgewandelt. Diese wird durch:

$E_{P}=m\cdot g\cdot h_{2}-m\cdot g\cdot h_{1}=m\cdot g\cdot h$

g ist hier die Fallbeschleunigung und h der Höhenunterschied h₂-h₁

Wir brauchen dann in der Gleichung (1) nur die potenzielle Energie mitberechnen:

$p_{L}\cdot \Delta V_{L}+{1 \over 2}\Delta m_{L}\cdot v_{L}^{2}=p_{R}\cdot \Delta V_{R}+{1 \over 2}\Delta m_{R}\cdot v_{R}^{2}+m\cdot g\cdot h\qquad (2)$

Diese ist die sogenannte bernoullische Druckgleichung bei einer idealer Strömung.