MathemaTriX ⋅ Mittlere Änderungsrate
Erscheinungsbild
| ||||||||||||||||||
LINKS
Zumindest eine Aufgabe probieren
Theorie in Kürze (mit Geogebra)
- y in Abhängigkeit von x, y in Bezug auf x, je x desto y
- Punkt (x|y), also erst x und dann y.
- Absolute Änderung: also nur die y-Änderung für die zwei angegebenen x-Werte. Also die x-Werte sind angegeben, die y-Werte muss man subtrahieren!
- Relative Änderung: keine Einheiten (kann man mit Kommaverschieben als Prozentsatz angeben). Die Differenz der y-Werte durch den ersten y-Wert.
- Mittlere Änderungsrate, auch Differenzenquotient.: Einheit: Einheiten der y-Achse pro eine Einheit der x-Achse. → Steigung der Gerade, die zwei Punkte verbindet.
Der Unterschied zwischen Änderungsrate und relativer Änderung ist daher der Nenner des Bruches.
- Ist er einer der beiden Werte des Zählers, dann geht es (fast immer) um eine relative Änderung.
- Ist er eine Differenz von Werten (der x-Achse), dann geht es um eine mittlere Änderungsrate (Steigung).
Die absolute Änderung hingegen ist (fast immer) kein Bruch sondern einfach eine Differenz von zwei (in der Regel y-) Werten.
- Ausdrücke
- Absolute Änderung: Der/Die/Das (Begriff, was auf der y-Achse steht) ist zwischen (was und ist) mehr/weniger geworden
- Relative Änderung: Der/Die/Das (Begriff, was auf der y-Achse steht) ist zwischen (was und ist) um so viel Prozent mehr/weniger geworden
- Mittlere Änderungsrate: Der/Die/Das (Begriff, was auf der y-Achse steht) ist zwischen (was und ist) durchschnittlich um (y-Einheiten pro EINE x-Einheit → Steigung) mehr/weniger geworden
- Wie viel war die absolute prozentuale Änderung für Blautrex zwischen 3. und 15. Minute?
- Wie viel war die mittlere prozentuale Änderung für Mavrit zwischen 3 und 23 Minute (mit Einheit)?
- Wie viel war die mittlere prozentuale Änderung für Linix zwischen 8 und 16 Minute? Interpretieren Sie das Ergebnis!

4 verschiedene Waschmittel wurden auf ihre Effektivität geprüft. Das Diagramm zeigt welcher Anteil (in Prozent) des Schmutzes geblieben ist in Bezug auf die Zeit (in Minuten).
- Wie viel ist die absolute Temperaturänderung zwischen 3 und 5,5 m?
- Wie viel ist die mittlere Temperaturänderung zwischen 1 und 4 m (mit Einheit)?
- Wie viel ist die mittlere Temperaturänderung zwischen 4 und 5 m? Interpretieren Sie das Ergebnis!
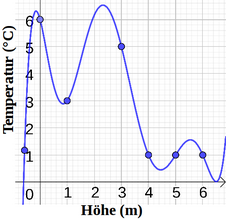
Das Diagramm stellt die Temperatur in einem Wassertank in Bezug auf seine Höhe dar.
- Wie viel ist das absolute Bevölkerungswachstum für die grüne Stadt für die ersten 20 Jahren?
- Wie viel ist das mittlere Bevölkerungswachstum für die schwarze Stadt für die ersten 60 Jahren? (mit Einheit)?
- Wie viel ist das mittlere Bevölkerungswachstum für die schwarze Stadt zwischen 60 und 90 Jahr? Interpretieren Sie das Ergebnis!

Das Wachstum der Bevölkerung (in Millionen) in 4 verschiedenen (imaginären) Städten in Abhängigkeit von der Zeit in Jahren wurde im Diagramm zusammengefasst.



















