Technisches Zeichnen/ Grundkonstruktionen

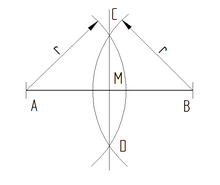
Halbieren einer Strecken, Errichten einer Mittelsenkrechten

• um A und B einen Kreisbogen mit den Radius $r>{\frac {\overline {AB}}{2}}$ schlagen
• die beiden entstandenen Schnittpunkte C und D verbinden

Mittelsenkrechte

Errichten einer Senkrechten im Endpunkt

Die Prinzipien der beiden folgenden Konstruktionen sind insbesondere bei eingeschränkten Platzverhältnissen anwendbar.

• um B einen Kreisbogen schlagen
• der Kreisbogen schneidet ${\overline {AB}}$ im Punkt C
• um C einen weiteren Kreisbogen mit dem selben Radius schlagen
• beide Kreisbogen schneiden sich im Punkt D
• um D noch einen Kreis mit dem selben Radius schlagen
• durch die Punkte C und D eine Gerade ziehen
• diese Gerade schneidet den Kreis um D im Punkt E
• die Punkte B und E verbinden

Senkrechte im Endpunkt

Eine mögliche Alternative

• wählen eines beliebigen Punktes M oberhalb der Halbggeraden h
• um M einen Kreisbogen mit dem Radius ${\overline {MP}}$ schlagen
• der Kreisbogen schneidet h im Punkt B
• ab B durch M eine Linie ziehen
• diese Linie schneidet den Kreisbogen in P'
• ab P durch P' eine Linie ziehen

Senkrechte im Endpunkt A, oder nahe daran, einer Halbgeraden h mittels  Thaleskreis errichten
Animation am Ende Pause 10 s

Fällen des Lotes

• um P einen Kreisbogen schlagen
• der Kreisbogen schneidet die Gerade in den Punkten A und B
• um A und B einen Kreisbogen mit dem selben Radius schlagen
• die Kreisbogen schneiden sich im Punkt C
• Schnittpunkt C und P verbinden

Lot fällen

Eine mögliche Alternative wenn P' nahe an A liegt

• wählen eines beliebigen Punktes B auf der Halbgeraden h
• die Punkte P und B verbinden
• um B und P einen Kreisbogen mit den Radius $r>{\frac {\overline {BP}}{2}}$ schlagen
• die beiden entstandenen Schnittpunkte C und D verbinden
• die Verbindungslinie schneidet ${\overline {BP}}$ im Punkt M
• um M einen Kreisbogen mit dem Radius ${\overline {MP}}$ schlagen
• der Kreisbogen schneidet h im Punkt P'
• ab P durch P' eine gerade Linie ziehen

Lot mittels  Thaleskreis fällen, Animation, am Ende Pause 10 s

Konstruktion einer Parallelen durch einen gegebenen Punkt (D)

• um einen beliebigen Punkt C auf ${\overline {AB}}$ einen Kreisbogen mit Radius $r={\overline {CD}}$ schlagen
• der Kreisbogen schneidet ${\overline {AB}}$ im Punkt E
• um D und E einen weiteren Kreisbogen mit dem selben Radius schlagen
• die Kreisbogen schneiden sich im Punkt F
• durch die Punkte D und F eine Gerade ziehen

Parallele durch Punkt

Teilen einer Strecke in gleich große Teile

• ausgehend von Punkt A eine Gerade in beliebigem Winkel zu ${\overline {AB}}$ zeichnen
• auf dieser Geraden mit dem Zirkel gleich große Abschnitte abtragen, deren Anzahl gleich der Anzahl der gewünschten Streckenteile ist
• den letzten so entstandenen Schnittpunkt C mit Punkt B verbinden
• durch die restlichen Schnittpunkte auf ${\overline {AC}}$ Parallelen zur Strecke ${\overline {BC}}$ ziehen

Gleiche Teile

Goldener Schnitt

• Strecke ${\overline {AB}}$ halbieren ergibt Punkt C
• in B eine Senkrechte errichten
• um Punkt B einen Kreisbogen mit dem Radius ${\overline {BC}}$ schlagen
• der Kreisbogen schneidet die Senkrechte im Punkt D
• die Punkte A und D verbinden
• um D einen Kreisbogen mit dem Radius ${\overline {BD}}$ schlagen
• der Kreisbogen schneidet ${\overline {AD}}$ im Punkt E
• um A einen Kreisbogen mit dem Radius ${\overline {AE}}$ schlagen
• der Kreisbogen schneidet ${\overline {AB}}$ im Punkt F
• $\Phi ={\overline {AB}}:{\overline {AF}}={\overline {AF}}:{\overline {FB}}={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618{\text{.}}$

Goldener Schnitt

Halbieren eines Winkels

• um A einen Kreisbogen mit beliebigem Radius schlagen
• der Kreisbogen schneidet die Schenkel des Winkels in den Punkten B und C
• um B und C den selben Kreisbogen schlagen
• diese Kreisbogen schneiden sich
• eine Gerade durch den Punkt A und den Schnittpunkt der beiden Kreisbogen ziehen

Winkel halbieren

90° Winkel in drei gleiche Teile teilen

• um A einen Kreisbogen mit beliebigem Radius schlagen
• der Kreisbogen schneidet die Schenkel des Winkels in den Punkten B und C
• um B und C den selben Kreisbogen schlagen
• diese Kreisbogen schneiden sich in den Punkten D und E
• die Punkte D und E mit A verbinden

90° Winkel dritteln

Konstruktion eines gleichseitigen Dreiecks

Bei gegebener Seitelänge

• um A und B einen Kreisbogen mit dem Radius $r={\overline {AB}}$ schlagen
• die Kreisbogen schneiden sich im Punkt C
• die Punkte A und B mit C verbinden

Gleichseitiges Dreieck

Bei gegebenem Umkreis

• zeichne eine Gerade durch den Umkreismittelpunkt M
• diese schneidet den Umkreis in den Punkten C und D
• schlage um Punkt D einen Kreisbogen mit dem Radius des Umkreises
• dieser Kreisbogen schneidet den Umkreis in A und B
• die Punkte A mit B sowie A und B mit C verbinden

Gleichseitiges Dreieck

Mittelpunkt eines Kreises konstruieren

• 2 nicht parallele Gerade durch den Kreis ziehen
• eine Gerade schneidet den Kreis in A und B die andere in A1 und B1
• auf den Sehnen ${\overline {AB}}$ und ${\overline {A1B1}}$ die Mittelsenkrechte errichten
• die Mittelsenkrechten schneiden sich im Mittelpunkt M

Kreismittelpunkt

Umkreis eines Dreiecks

• auf 2 beliebigen Dreiecksseiten die Mittelsenkrechte errichten
• die Mittelsenkrechten schneiden sich im Punkt M
• um M einen Kreisbogen schlagen, der die Punkte A, B und C schneidet

Umkreis

Inkreis eines Dreiecks

• 2 beliebige Winkel des Dreiecks halbieren
• die Winkelhalbierenden schneiden sich im Punkt M
• um M einen Kreisbogen schlagen, der die Dreiecksseiten berührt

Inkreis

Tangente über einen Kreispunkt konstruieren

• Punkt P mit Kreismittelpunkt M verbinden
• auf ${\overline {MP}}$ im Punkt P die Senkrechte errichten

Tangente 1

Tangente über einen Punkt außerhalb eines Kreises konstruieren

• Punkt P mit Kreismittelpunkt M verbinden
• Kreisbogen mit dem Radius $r={\frac {\overline {MP}}{2}}$ über ${\overline {MP}}$ schlagen
• dieser Kreisbogen schneidet den Kreis im Punkt A
• die Punkte A und P verbinden

Tangente 2

Zeichnerische Ermittlung des Kreisumfanges

Näherungskonstruktion
halber Umfang 1

Näherungskonstruktion
halber Umfang 2

Konstruktion regelmäßiger Vielecke

Fünfeck

Konstruktion Fünfeck
daraus Zehneck

Sechseck

Konstruktion Sechseck
daraus Zwölfeck

Siebeneck

Näherungskonstruktion Siebeneck

Achteck

Konstruktion Achteck
aus Viereck