Astronomische Berechnungen für Amateure/ Distanzen/ Erdnaher Raum

Distanzbestimmungen gehören in der Astronomie zu den schwierigen Aufgaben. Es ist auch bezeichnend, dass man von „Bestimmung“ und nicht von „Messung“ spricht. Als zweite Erschwernis kommt hinzu, dass die Zahlenwerte rasch unvorstellbar groß werden. Die „astronomischen Werte“ sind ein stehender Begriff unserer Sprache. Der erdnahe Raum ist ein Bereich, wo die Werte noch vorstellbare Grössenordnungen haben. Wo dieser erdnahe Raum beginnt und wo er endet ,ist eine Definitionsfrage. Wir wollen recht pragmatisch von bis ca. 10 Million Kilometer Abstand von der Erde ausgehen. Wie schon diese Festlegung zeigt, verwenden wir in diesem Bereich des Kosmos die aus dem Alltag bekannten Längeneinheiten.

In diesem Teil des Weltalls interessieren vor allem die folgenden Objekte:

• Meteore und Feuerkugeln, die in den obersten Schichten der Atmosphäre Leuchterscheinungen hervorrufen.

• Künstliche Satelliten, die die Erde umkreisen, wie z. B. die internationale Raumstation ISS oder die GPS-Satelliten, um zwei Beispiele zu nennen.

• Die erdnahen Objekte (Near Earth Objects NEO) oder präziser die erdnahen Asteroiden NEA, die im schlimmsten Fall sogar mit der Erde kollidieren können.

• Nicht zu vergessen: Unser Mond bewegt sich in diesem Bereich.

Für unser Thema Berechnungen sind die folgenden Fragen von Interesse:

• Höhenbestimmungen – dazu benötigt man Methoden der Sphärischen Astronomie, auf die wir im folgenden Kapitel eingehen werden

• Bahnbestimmungen – ein Thema für die Himmelsmechanik im übernächsten Kapitel

• Bestimmung der täglichen Parallaxe

Äquatorial-Horizontalparallaxe π bzw. tägliche Parallaxe p eines Objektes O in geozentrischer Distanz Δ

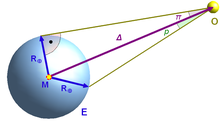
Mit dem Begriff tägliche Parallaxe bezeichnen wir folgendes Phänomen: Auf die Erde bezogene Angaben verwenden den Erdmittelpunkt als Referenz („geozentrische Position“). Gerade für Objekte im erdnahen Raum kann aber auch bei nicht sehr genauen Rechnungen nicht vernachlässigt werden, dass der Beobachter nicht im Erdmittelpunkt, sondern auf der Erdoberfläche sitzt („topozentrische Position“) und somit ein Richtungsunterschied zu einem (fiktiven) Beobachter im Erdzentrum besteht. Diesen Unterschied nennt man die tägliche Parallaxe. Hat der betrachtete Himmelskörper vom Erdmittelpunkt den geozentrischen Abstand Δ (in km) und beträgt der Erdradius $R_{\oplus }\;\approx \;6378\;{\text{km}}$, dann berechnet sich der Parallaxenwinkel π wie folgt:

$\sin \pi \quad =\quad {\frac {R_{\oplus }}{\Delta }}\quad \approx \quad {\frac {6378\;{\text{km}}}{\Delta }}$

Dies ist die grösstmögliche Verschiebung eines Himmelskörpers vor dem Sternenhintergrund. Sie wird auch als Äquatorial-Horizontalparallaxe bezeichnet. Wie gross die wirkliche Parallaxe p ist, werden Sie sehen, wenn im nächsten Kapitel die Koordinatensysteme behandelt werden.

Die Entfernung bestimmt zusammen mit dem wahren Radius auch den scheinbaren Radius bzw. den scheinbaren Durchmesser eines Objektes am Erdhimmel. Wenn wiederum Δ der geozentrische Abstand des Himmelskörpers und R sein Radius ist (beide in km), s der scheinbare Radius bzw. D der scheinbare Durchmesser des Himmelskörpers am Erdhimmel (beide in ° oder '), so lautet der Zusammenhang:

$\sin s\quad =\quad {\frac {R}{\Delta }}\;{\text{;}}\qquad D\quad =\quad 2\cdot s$

Übungen

• Wie gross ist die Horizontalparallaxe des Mondes in seiner durchschnittlichen Entfernung von 384 400 km, in seiner Perigäumstellung von 356 400 km und in der Apogäumstellung von 406 700 km?

• Wie gross ist die Horizontalparallaxe eines Himmelskörpers, der sich an der Grenze des von uns als „erdnahen Raum“ bezeichneten Gebietes bewegt?

• Wie müssen Erde, Beobachter und Himmelskörper zueinander stehen, dass der Beobachter keine parallaktische Verschiebung des Himmelskörpers feststellen kann? Wie müssen sie zueinander stehen, damit gerade die Horizontalparallaxe (also die grösstmögliche parallaktische Verschiebung) beobachtet werden kann?

• Nehmen Sie das Beispiel Mond: Welche anschauliche Bedeutung hat die auf der Erde gemessene Horizontalparallaxe für einen Beobachter auf dem Mond (z. B. für einen Astronauten)?

• Welchen scheinbaren Radius bzw. Durchmesser hat der Mond (R = 1738 km) in mittlerer, erdnaher und erdferner Position?

• In welcher Position ist der scheinbare Durchmesser des Mondes grösser: Wenn er am Horizont steht oder wenn er im Zenit steht?

Hoch zu Inhaltsverzeichnis | Vor zu Das Sonnensystem; Lichtzeit