Die Ableitung einer Funktion ist durch folgende Gleichung definiert:

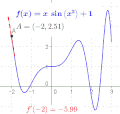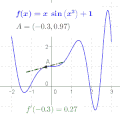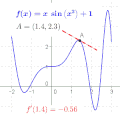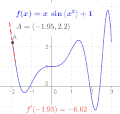
Die Funktion  geht durch den Punkt
geht durch den Punkt  . Zeichnet man in diesem Punkt die Tangente an die Funktion und misst deren Steigung aus, so erhält man gerade den Wert
. Zeichnet man in diesem Punkt die Tangente an die Funktion und misst deren Steigung aus, so erhält man gerade den Wert  . Die Ableitung hat also die anschauliche Bedeutung der
Tangentensteigung. Sucht man eine Gerade die durch den Punkt
. Die Ableitung hat also die anschauliche Bedeutung der
Tangentensteigung. Sucht man eine Gerade die durch den Punkt  geht und deren Funktionswerte in einem kleinen Bereich um x herum möglichst nahe an denen von
geht und deren Funktionswerte in einem kleinen Bereich um x herum möglichst nahe an denen von  liegen soll, so erhält man gerade die Tangente. Man nennt die Tangente daher auch lineare Bestapproximation. Zur Berechnung der Ableitungen gibt es einige Regeln, die im Folgenden nachgerechnet werden.
Es gibt viele unterschiedliche Schreibweisen für Ableitungen, einige von diesen sind:
liegen soll, so erhält man gerade die Tangente. Man nennt die Tangente daher auch lineare Bestapproximation. Zur Berechnung der Ableitungen gibt es einige Regeln, die im Folgenden nachgerechnet werden.
Es gibt viele unterschiedliche Schreibweisen für Ableitungen, einige von diesen sind:

Sie sind alle gleichwertig. Weiterhin gibt es noch die Schreibweise:

In viele Fällen ist sie den obigen Schreibweisen gleichwertig. Jedoch gilt es insbesondere im mehrdimensionalen Fall Unterschiede zwischen diesen beiden Schreibweisen zu beachten, so dass häufig gilt:

Aber dies soll uns hier noch nicht belasten. Man kann jeder differenzierbaren Funktion ihre Ableitung zuordnen. Damit hat man dann eine Abbildung von der Menge der Funktionen in die Menge der Funktionen. Für diese Abbildung schreibt man auch das Symbol  . Es handelt sich also um ein Rechenzeichen das aus einer Funktion deren Ableitung berechnet. Diese Art von Rechenzeichen nennt man auch Differenzialoperatoren.
Natürlich ist auch
. Es handelt sich also um ein Rechenzeichen das aus einer Funktion deren Ableitung berechnet. Diese Art von Rechenzeichen nennt man auch Differenzialoperatoren.
Natürlich ist auch  ein Differenzialoperator. Erfunden wurde die Differentialrechnung von Isaac Newton und Gottfried Wilhelm Leibniz.
ein Differenzialoperator. Erfunden wurde die Differentialrechnung von Isaac Newton und Gottfried Wilhelm Leibniz.



Betrachten wir die identische Abbildung  :
:

Dies ist nicht verwunderlich da jede Tangente an eine Gerade mit der Steigung 1 ebenfalls die Steigung 1 hat.
Betrachten wir die Funktion  wobei
wobei  :
Die Ableitung ist gegeben durch:
:
Die Ableitung ist gegeben durch:

Dies zeigen wir per Induktion. Mit der Berechnung der Ableitung der Funktion  haben wir diese Formel schon für
haben wir diese Formel schon für  bewiesen. Es bleibt also nur noch der Induktionsschritt von
bewiesen. Es bleibt also nur noch der Induktionsschritt von  auf
auf  . Sei die Formel für
. Sei die Formel für  schon bewiesen:
Dann berechnet sich die Ableitung von
schon bewiesen:
Dann berechnet sich die Ableitung von  nach der Produktregel:
nach der Produktregel:

Damit ist die Aussage für alle  bewiesen.
bewiesen.
Betrachten wir die konstante Funktion  :
:

Die Ableitung der konstanten Funktion ist also 0. Betrachten wir nun eine beliebige Funktion multipliziert mit einer Konstanten.

Man darf Konstanten also einfach vor die Ableitung ziehen.

Die Ableitung der Exponentialfunktion

berechnet sich nach obigen Regeln zu:

Sie geht also beim Ableiten in sich selbst über.
Für  gilt:
gilt:

 ist hier der natürliche Logarithmus.
ist hier der natürliche Logarithmus.
Übung: Leiten Sie  her. Eine Lösung der Übung findet sich z.B.
her. Eine Lösung der Übung findet sich z.B.  auf Wikipedia.
auf Wikipedia.

Sei  eine beliebige Funktion und g die zugehörige Umkehrfunktion dann gilt offensichtlich:
eine beliebige Funktion und g die zugehörige Umkehrfunktion dann gilt offensichtlich:

Leitet man beide Seiten ab so erhält man:

Wendet man das obige Ergebnis mit  und
und  an so hat man:
an so hat man:

und somit

Die Ableitung des Logarithmus  ist also die Funktion
ist also die Funktion  . Dir Funktion
. Dir Funktion  sei hier der natürliche Logarithmus!
sei hier der natürliche Logarithmus!
Für einen Logarithmus zur Basis a gilt allgemein:

Übung: Leiten Sie  her.
her.
Beispiel: Etwas vertrackt ist die Ableitung von  . Dazu erweitern wir den Ausdruck
. Dazu erweitern wir den Ausdruck
 .
.
Wer das nicht glaubt, der prüfe das Ergebnis mit einem Computeralgebrasystem nach (hier z.B. mit Maxima). Einfach folgenden Ausdruck eingeben und auswerten lassen:
diff(x**x, x);
Es wird natürlich das händisch ausgerechnete Ergebnis geliefert.
Übung: Berechnen Sie  .
.
Wie wir im Kapitel über komplexe Zahlen sahen ist:

und

Die Ableitungen berechnen sich nach den oben angebenen Regeln zu:

und

Wobei wir im letzten Schritt  benutzt haben. Ansonsten haben wir mit komplexen Zahlen und Funktionen genauso gerechnet wie mit reellen, aber das dürfen wir auch.
benutzt haben. Ansonsten haben wir mit komplexen Zahlen und Funktionen genauso gerechnet wie mit reellen, aber das dürfen wir auch.
Der Tangens ist bekanntlich definert durch:
 Die Ableitung ergibt sich nach den obigen Regeln zu
Die Ableitung ergibt sich nach den obigen Regeln zu

Übung: Leiten Sie die Ableitungen von  her. Lösungshinweis: Diese Funktionen sind Umkehrfunktionen der trigonometrischen Funktionen.
her. Lösungshinweis: Diese Funktionen sind Umkehrfunktionen der trigonometrischen Funktionen.
Ist die Ableitung einer Funktion wieder ableitbar, so erhält man höhere Ableitungen. Z.B. ist die Ableitung der ersten Ableitung die zweite Ableitung:
 .
.
Und so geht es weiter mit der dritten Ableitung  , der vierten Ableitung
, der vierten Ableitung  usw.
usw.
Beispiel: Die 2. Ableitung  von
von  soll berechnet werden.
soll berechnet werden.


Übungen:
 , bestimmen Sie
, bestimmen Sie 
 , bestimmen Sie
, bestimmen Sie 
 , bestimmen Sie
, bestimmen Sie 
- Bestimme den Definitionsbereich der Funktion (
 Definitionsmenge)
Definitionsmenge)
- Bestimme, ob die Funktion symmetrisch oder antisymmetrisch ist
- Bestimme die Nullstellen von
 und somit
und somit
 Funktion ist positiv
Funktion ist positiv Funktion ist streng monoton wachsend
Funktion ist streng monoton wachsend Funktion ist konvex (
Funktion ist konvex ( Konvexe und konkave Funktionen)
Konvexe und konkave Funktionen) Funktion ist negativ
Funktion ist negativ Funktion ist streng monoton fallend
Funktion ist streng monoton fallend Funktion ist konkav
Funktion ist konkav
- Bestimme die Extremstellen (
 Extremwert)
Extremwert)

 lokales Minimum
lokales Minimum lokales Maximum
lokales Maximum
- Bestimme die Wendepunkte (
 Wendepunkt)
Wendepunkt)

- Bestimme ggf. die Pole (
 Polstelle)
Polstelle)
- Bestimme ggf. die Asymptoten (
 Asymptote)
Asymptote)
Beispiel: 
Definitionsbereich: 
Nullstelle(n): 
Symmetrisch/antisymmetrisch: nein (siehe z.B. den Graphen der Funktion)
Extremstellen: 

 ; d.h. die Extremstelle bei
; d.h. die Extremstelle bei  ist ein Maximum.
ist ein Maximum.
Wendepunkte:  ; lt. Graphen ist das ein Wendepunkt (ggf.
; lt. Graphen ist das ein Wendepunkt (ggf.  berechnen).
berechnen).
Pol(e): 
Siehe auch  Kurvendiskussion.
Kurvendiskussion.
Übungen: Diskutieren Sie folgende Kurven




 ist das Restglied. Es gibt mehrere Möglichkeiten dieses zu berechnen.
ist das Restglied. Es gibt mehrere Möglichkeiten dieses zu berechnen.
- Schlömilchsche Restgliedformel:

 und zwischen 1 und n+1;
und zwischen 1 und n+1;  zwischen
zwischen  und
und 
- Lagrangesche Restgliedformel: Für

- Cauchysche Restgliedformel: Für

Im Spezialfall  wird die Taylorreihe auch Maclaurin-Reihe genannt.
wird die Taylorreihe auch Maclaurin-Reihe genannt.
-
Brook Taylor (1685 - 1731) britischer Mathematiker
-
Oscar Xavier Schlömilch (1823 - 1901) deutscher Mathematiker
-
Joseph-Louis de Lagrange (1736 - 1813) italienisch-französischer Mathematiker
-
Augustin-Louis Cauchy (1789 - 1857) französischer Mathematiker
-
Colin Maclaurin (1698 - 1746) schottischer Mathematiker
Beispiel: Wir entwickeln die Taylorreihe um 0 für die Funktion 



 (lt. Lagrange)
(lt. Lagrange)
Übungen:
- Berechnen Sie die Taylorreihe um 0 für die Funktion

- Berechnen Sie die Taylorreihe um 1 für die Funktion

Siehe auch  Taylorreihe.
Taylorreihe.
-
Guillaume François Antoine, Marquis de L’Hospital (1661 - 1704) französischer Mathematiker
-
Johann Bernoulli (1667 - 1748) schweizer Mathematiker, der eigentliche Entdecker dieser Regel
 Regel von de L’Hospital: ... Die Regel von de L’Hospital erlaubt es in vielen Fällen, den Grenzwert von Funktionen selbst dann noch zu bestimmen, wenn deren Funktionsterm beim Erreichen der betreffenden Grenze einen unbestimmten Ausdruck wie etwa
Regel von de L’Hospital: ... Die Regel von de L’Hospital erlaubt es in vielen Fällen, den Grenzwert von Funktionen selbst dann noch zu bestimmen, wenn deren Funktionsterm beim Erreichen der betreffenden Grenze einen unbestimmten Ausdruck wie etwa  liefert...
liefert...
Es sei also

oder
 und
und  .
.
Es gilt dann
 .
.
Liefert diese Ableitung noch kein Ergebnis, so kann auch mehrfach abgeleitet werden - bis sich ein bestimmter Ausdruck ergibt.
Beispiel:  . Das gibt einen Ausdruck vom Typ
. Das gibt einen Ausdruck vom Typ  . Leiten wir die Funktionen (im Nenner und im Zähler) einmal ab, so ergibt sich
. Leiten wir die Funktionen (im Nenner und im Zähler) einmal ab, so ergibt sich  .
.
Beispiel:  ist vom Typ
ist vom Typ  . Bringen wir das auf gleichen Nenner, so ergibt sich
. Bringen wir das auf gleichen Nenner, so ergibt sich  . Das ist vom Typ
. Das ist vom Typ  . Leiten wir einmal ab, so erhalten wir
. Leiten wir einmal ab, so erhalten wir  . Das ist wieder vom Typ
. Das ist wieder vom Typ  . Nochmals ableiten ergibt
. Nochmals ableiten ergibt  .
.
Übungen: