implizit:
F
(
x
,
y
)
=
0
{\displaystyle F(x,y)=0}
explizit:
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
=
x
(
t
)
;
y
=
y
(
t
)
{\displaystyle x=x(t);\;y=y(t)}
r
=
f
(
ϕ
)
{\displaystyle r=f(\phi )}
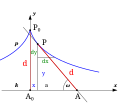
Ein Weg heißt rektifizierbar (streckbar), wenn folgendes gilt:
L
∈
R
0
+
{\displaystyle L\in \mathbb {R} _{0}^{+}}
L
{\displaystyle L}
Siehe auch Weg (Mathematik)
Sei
r
(
t
)
=
[
x
(
t
)
y
(
t
)
]
{\displaystyle \mathbf {r} (t)={\begin{bmatrix}x(t)\\y(t)\end{bmatrix}}}
L
(
r
)
=
∫
a
b
|
r
˙
|
d
t
=
∫
a
b
x
˙
2
+
y
˙
2
d
t
{\displaystyle L(\mathbf {r} )=\int _{a}^{b}|{\dot {\mathbf {r} }}|\ \mathrm {d} t=\int _{a}^{b}{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}\mathrm {d} t}
Dies lässt sich auch so schreiben:
L
=
∫
a
b
x
˙
2
+
y
˙
2
d
t
=
∫
a
b
x
˙
1
+
(
y
˙
x
˙
)
2
d
t
=
∫
a
b
1
+
(
d
y
d
t
d
t
d
x
)
2
d
x
d
t
d
t
=
∫
a
b
1
+
(
y
′
)
2
d
x
{\displaystyle L=\int _{a}^{b}{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}\mathrm {d} t=\int _{a}^{b}{\dot {x}}{\sqrt {1+\left({\frac {\dot {y}}{\dot {x}}}\right)^{2}}}\mathrm {d} t=\int _{a}^{b}{\sqrt {1+\left({\frac {\mathrm {d} y\ \mathrm {d} t}{\mathrm {d} t\ \mathrm {d} x}}\right)^{2}}}{\frac {\mathrm {d} x}{\mathrm {d} t}}\mathrm {d} t=\int _{a}^{b}{\sqrt {1+(y')^{2}}}\mathrm {d} x}
Siehe auch Länge_(Mathematik)
Bekanntlich ist der Flächeninhalt durch das Integral
A
=
∫
x
0
x
1
y
d
x
{\displaystyle A=\int _{x_{0}}^{x_{1}}y\mathrm {d} x}
d
t
d
t
{\displaystyle {\frac {\mathrm {d} t}{\mathrm {d} t}}}
A
=
∫
x
0
x
1
y
d
x
=
∫
y
d
t
d
t
d
x
=
∫
t
0
t
1
y
x
˙
d
t
{\displaystyle A=\int _{x_{0}}^{x_{1}}y\mathrm {d} x=\int y{\frac {\mathrm {d} t}{\mathrm {d} t}}\mathrm {d} x=\int _{t_{0}}^{t_{1}}y{\dot {x}}dt}
Ist die Kurve die gezeichnete geschlossene doppelpunktfreie Kurve (auch geschlossene Jordankurve
Beispiel: Wir berechnen den Flächeninhalt einer Ellipse
x
=
a
cos
t
;
y
=
b
sin
t
;
a
,
b
∈
R
+
{\displaystyle x=a\cos t;\;y=b\sin t;\;a,b\in \mathbb {R} ^{+}}
x
˙
=
−
a
sin
t
{\displaystyle {\dot {x}}=-a\sin t}
Wir müssen hier aufpassen, die Drehrichtung muss im Uhrzeigersinn sein. Somit gilt
∫
2
π
0
x
˙
y
d
t
=
−
a
b
∫
2
π
0
sin
2
t
d
t
=
−
a
b
[
1
2
t
−
1
4
sin
(
2
t
)
]
2
π
0
=
a
b
π
{\displaystyle \int _{2\pi }^{0}{\dot {x}}y\mathrm {d} t=-ab\int _{2\pi }^{0}\sin ^{2}t\mathrm {d} t=-ab\left[{\frac {1}{2}}t-{\frac {1}{4}}\sin(2t)\right]_{2\pi }^{0}=ab\pi }
Die Krümmung sei definiert als
κ
=
d
ϕ
d
s
{\displaystyle \kappa ={\frac {\mathrm {d} \phi }{\mathrm {d} s}}}
r
˙
=
[
x
˙
y
˙
]
{\displaystyle {\dot {\mathbf {r} }}={\begin{bmatrix}{\dot {x}}\\{\dot {y}}\end{bmatrix}}}
ϕ
=
arctan
y
˙
x
˙
{\displaystyle \phi =\arctan {\frac {\dot {y}}{\dot {x}}}}
d
ϕ
d
t
=
1
1
+
(
y
˙
x
˙
)
2
⏟
aus Ableitungstafel
y
¨
x
˙
−
x
¨
y
˙
x
˙
2
⏟
innere Ableitung
{\displaystyle {\frac {\mathrm {d} \phi }{\mathrm {d} t}}=\underbrace {\frac {1}{1+\left({\frac {\dot {y}}{\dot {x}}}\right)^{2}}} _{\text{aus Ableitungstafel}}\underbrace {\frac {{\ddot {y}}{\dot {x}}-{\ddot {x}}{\dot {y}}}{{\dot {x}}^{2}}} _{\text{innere Ableitung}}}
d
s
d
t
=
|
r
˙
|
=
x
˙
2
+
y
˙
2
{\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} t}}=|{\dot {\mathbf {r} }}|={\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}}
κ
=
d
ϕ
d
s
=
d
ϕ
d
t
d
t
d
s
=
x
˙
y
¨
−
x
¨
y
˙
(
x
˙
2
+
y
˙
2
)
3
2
{\displaystyle \kappa ={\frac {\mathrm {d} \phi }{\mathrm {d} s}}={\frac {\mathrm {d} \phi }{\mathrm {d} t}}{\frac {\mathrm {d} t}{\mathrm {d} s}}={\frac {{\dot {x}}{\ddot {y}}-{\ddot {x}}{\dot {y}}}{({\dot {x}}^{2}+{\dot {y}}^{2})^{\frac {3}{2}}}}}
Weiters gilt:
κ
=
y
″
(
1
+
(
y
′
)
2
)
3
2
{\displaystyle \kappa ={\frac {y''}{(1+(y')^{2})^{\frac {3}{2}}}}}
Man kann nun noch Links- (
κ
>
0
{\displaystyle \kappa >0}
κ
<
0
{\displaystyle \kappa <0}
Der Krümmungsradius ist definiert zu
ρ
=
1
|
κ
|
{\displaystyle \rho ={\frac {1}{|\kappa |}}}
Übungen: Bestimmen Sie die Krümmungsradien der folgenden Kurven
Neilsche Parabel:
x
=
t
2
;
y
=
t
3
{\displaystyle x=t^{2};\;y=t^{3}}
y
=
x
4
{\displaystyle y=x^{4}}
Der Tangenteneinheitsvektor berechnet sich zu
T
=
r
˙
|
r
˙
|
=
1
x
˙
2
+
y
˙
2
⏟
1
/
|
r
˙
|
[
x
˙
y
˙
]
⏟
r
˙
{\displaystyle \mathbf {T} ={\frac {\mathbf {\dot {r}} }{|\mathbf {\dot {r}} |}}=\underbrace {\frac {1}{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}} _{1/|\mathbf {\dot {r}} |}\underbrace {\begin{bmatrix}{\dot {x}}\\{\dot {y}}\end{bmatrix}} _{\mathbf {\dot {r}} }}
Der Normalenvektor kann über das rechtwinkelige Komplement ermittelt werden.
T
=
1
x
˙
2
+
y
˙
2
[
x
˙
y
˙
]
{\displaystyle \mathbf {T} ={\frac {1}{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}}{\begin{bmatrix}{\dot {x}}\\{\dot {y}}\end{bmatrix}}}
N
=
1
x
˙
2
+
y
˙
2
[
−
y
˙
x
˙
]
{\displaystyle \mathbf {N} ={\frac {1}{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}}{\begin{bmatrix}-{\dot {y}}\\{\dot {x}}\end{bmatrix}}}
Siehe auch Wendepunkt
Siehe auch Scheitelpunkt
Eine Evolvente ist laut Wikipedia (siehe Evolvente
... Anschaulich lässt sich die Evolvente als Fadenlinie darstellen: Ein flacher Körper, dessen eine Seitenfläche die Form der Ausgangskurve hat, wird auf ein Blatt Papier gelegt. Über die Ausgangskurve ist ein dünner Faden gewickelt und straff gespannt. Am äußeren Ende des Fadens wird ein Stift befestigt, dessen Spitze auf dem Papier aufliegt. Dann wird der Faden langsam von der Kurve abgewickelt, wobei er stets straff gehalten wird. Die Kurve, die auf dem Papier entsteht, ist eine Evolvente...
Eine Evolute lässt sich lt. Wikipedia auf verschiedene Weisen definieren (siehe Evolute
Sie ist die Bahn, auf der sich der Mittelpunkt des Krümmungskreises der Kurve bewegt, wenn dieser die gesamte Kurve durchläuft. Sie ist die die Hüllkurve (Enveloppe) der Normalen der gegebenen Kurve. Eine Kurve ist die Evolute jeder ihrer Evolventen. Parameterdarstellung der Evolute:
ξ
=
[
ξ
η
]
=
r
+
N
κ
=
[
x
y
]
+
(
x
˙
2
+
y
˙
2
)
3
/
2
y
¨
x
˙
−
x
¨
y
˙
[
−
y
˙
x
˙
]
x
˙
2
+
y
˙
2
{\displaystyle {\boldsymbol {\xi }}={\begin{bmatrix}\xi \\\eta \end{bmatrix}}=\mathbf {r} +{\frac {\mathbf {N} }{\kappa }}={\begin{bmatrix}x\\y\end{bmatrix}}+{\frac {({\dot {x}}^{2}+{\dot {y}}^{2})^{3/2}}{{\ddot {y}}{\dot {x}}-{\ddot {x}}{\dot {y}}}}{\frac {\begin{bmatrix}-{\dot {y}}\\{\dot {x}}\end{bmatrix}}{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}}}
ξ
=
x
−
y
˙
x
˙
2
+
y
˙
2
y
¨
x
˙
−
x
¨
y
˙
{\displaystyle \xi =x-{\dot {y}}{\frac {{\dot {x}}^{2}+{\dot {y}}^{2}}{{\ddot {y}}{\dot {x}}-{\ddot {x}}{\dot {y}}}}}
η
=
y
+
x
˙
x
˙
2
+
y
˙
2
y
¨
x
˙
−
x
¨
y
˙
{\displaystyle \eta =y+{\dot {x}}{\frac {{\dot {x}}^{2}+{\dot {y}}^{2}}{{\ddot {y}}{\dot {x}}-{\ddot {x}}{\dot {y}}}}}
Besondere Bedeutung haben Evolventen in der Technik im Bereich der Zahnräder (Evolventenverzahnung
Siehe auch Zykloide
Die gewöhnliche Zykloide (auch als gespitze Zykloide bezeichnet) ist die Bahn, die ein Punkt auf dem Umfang eines Kreises beschreibt, wenn dieser Kreis auf einer Geraden abrollt. Sie gehört zu den Rollkurven.
Parametergleichung: t heißt auch Wälzwinkel.
x
=
r
t
−
c
sin
t
;
x
=
r
−
c
sin
t
;
t
∈
R
{\displaystyle x=rt-c\sin t;\;x=r-c\sin t;\;t\in \mathbb {R} }
c
=
r
⇒
{\displaystyle c=r\Rightarrow }
0
<
c
<
r
⇒
{\displaystyle 0<c<r\Rightarrow }
c
>
r
⇒
{\displaystyle c>r\Rightarrow }
Zykloiden sind Trochoiden.
Bedeutung haben Zykloiden im Bereich der Getriebetechnik (siehe z.B. Zahnrad#Zykloidenverzahnung Zykloidgetriebe
Zykloidenverzahnung
Zykloidgetriebe
Aus der Parametergleichung finden wir:
x
˙
=
r
−
c
cos
t
;
y
˙
=
−
c
sin
t
{\displaystyle {\dot {x}}=r-c\cos t;\;{\dot {y}}=-c\sin t}
L
=
∫
0
2
π
x
˙
2
+
y
˙
2
d
t
=
∫
0
2
π
(
r
−
c
cos
t
)
2
+
c
2
sin
2
t
d
t
=
∫
0
2
π
r
2
−
2
r
c
cos
t
+
c
2
cos
2
t
+
c
2
sin
2
t
d
t
=
∫
0
2
π
r
2
+
c
2
−
2
r
c
cos
t
d
t
{\displaystyle {\begin{aligned}L=\int _{0}^{2\pi }{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}\mathrm {d} t=\int _{0}^{2\pi }{\sqrt {(r-c\cos t)^{2}+c^{2}\sin ^{2}t}}\mathrm {d} t=\\\int _{0}^{2\pi }{\sqrt {r^{2}-2rc\cos t+c^{2}\cos ^{2}t+c^{2}\sin ^{2}t}}\mathrm {d} t=\int _{0}^{2\pi }{\sqrt {r^{2}+c^{2}-2rc\cos t}}\mathrm {d} t\end{aligned}}}
Mit einer kleinen Umformung führt dies auf eine elliptische Gleichung, die nicht elementar zu lösen ist.
Z.B. aus einer Formelsammlung erhält man folgende Gleichung
sin
2
u
=
1
2
(
1
−
cos
2
u
)
{\displaystyle \sin ^{2}u={\frac {1}{2}}(1-\cos 2u)}
Für
u
=
t
2
{\displaystyle u={\frac {t}{2}}}
cos
t
=
1
−
2
sin
2
(
t
2
)
{\displaystyle \cos t=1-2\sin ^{2}\left({\frac {t}{2}}\right)}
L
=
∫
0
2
π
(
r
−
c
)
2
+
4
r
c
sin
2
t
2
d
t
{\displaystyle L=\int _{0}^{2\pi }{\sqrt {(r-c)^{2}+4rc\sin ^{2}{\frac {t}{2}}}}\mathrm {d} t}
Ist aber der Sonderfall einer gewöhnlichen Zykloide gegeben (
r
=
c
{\displaystyle r=c}
L
=
2
r
∫
0
2
π
sin
t
2
d
t
=
⏟
z.B. durch Substitution
−
4
r
cos
t
2
|
0
2
π
=
−
4
r
[
c
o
s
π
⏟
−
1
−
cos
0
⏟
1
]
=
8
r
{\displaystyle L=2r\int _{0}^{2\pi }\sin {\frac {t}{2}}\mathrm {d} t\underbrace {=} _{\text{z.B. durch Substitution}}-4r\cos {\frac {t}{2}}|_{0}^{2\pi }=-4r[\underbrace {cos\pi } _{-1}-\underbrace {\cos 0} _{1}]=8r}
A
=
−
∫
0
2
π
y
˙
x
d
t
=
−
∫
0
2
π
c
sin
t
(
r
t
−
c
sin
t
)
d
t
=
−
r
c
∫
0
2
π
t
sin
t
d
t
+
c
2
∫
0
2
π
sin
2
t
d
t
=
−
r
c
[
sin
t
−
t
cos
t
]
0
2
π
+
c
2
[
1
2
t
−
1
4
sin
(
2
t
)
]
0
2
π
=
2
r
c
π
+
c
2
π
=
π
(
2
r
c
+
c
2
)
{\displaystyle {\begin{aligned}A=-\int _{0}^{2\pi }{\dot {y}}x\mathrm {d} t=-\int _{0}^{2\pi }c\sin t(rt-c\sin t)\mathrm {d} t=-rc\int _{0}^{2\pi }t\sin t\mathrm {d} t+c^{2}\int _{0}^{2\pi }\sin ^{2}t\mathrm {d} t=\\-rc[\sin t-t\cos t]_{0}^{2\pi }+c^{2}[{\frac {1}{2}}t-{\frac {1}{4}}\sin(2t)]_{0}^{2\pi }=2rc\pi +c^{2}\pi =\pi (2rc+c^{2})\end{aligned}}}
Für die gewöhnliche Zykloide gilt somit:
A
=
3
r
2
π
{\displaystyle A=3r^{2}\pi }
gewöhnliche Epizykloide
verkürzte Epizykloide
Eine Kreisscheibe 1 rollt außen auf einer anderen Kreisscheibe 2 ab. Ein auf der Kreisscheibe 1 festgelegter Punkt beschreibt dann eine Epizykloide.
Es soll die Parametergleichung der gewöhnlichen Epizykloide mit Hilfe der Vektorrechnung hergeleitet werden:
p
=
[
x
y
]
=
R
+
r
=
[
R
cos
α
R
sin
α
]
+
[
r
cos
(
α
+
β
−
π
)
r
sin
(
α
+
β
−
π
)
]
=
[
R
cos
α
R
sin
α
]
−
[
r
cos
(
α
+
β
)
r
sin
(
α
+
β
)
]
{\displaystyle \mathbf {p} ={\begin{bmatrix}x\\y\end{bmatrix}}=\mathbf {R} +\mathbf {r} ={\begin{bmatrix}R\cos \alpha \\R\sin \alpha \end{bmatrix}}+{\begin{bmatrix}r\cos(\alpha +\beta -\pi )\\r\sin(\alpha +\beta -\pi )\end{bmatrix}}={\begin{bmatrix}R\cos \alpha \\R\sin \alpha \end{bmatrix}}-{\begin{bmatrix}r\cos(\alpha +\beta )\\r\sin(\alpha +\beta )\end{bmatrix}}}
Es gilt auch
R
α
=
r
β
⇒
β
=
R
r
α
{\displaystyle R\alpha =r\beta \Rightarrow \beta ={\frac {R}{r}}\alpha }
Eingesetzt ergibt sich die Parameterform
x
=
(
R
+
r
)
cos
α
−
r
cos
(
(
1
+
R
r
)
α
)
{\displaystyle x=(R+r)\cos \alpha -r\cos \left(\left(1+{\frac {R}{r}}\right)\alpha \right)}
y
=
(
R
+
r
)
sin
α
−
r
sin
(
(
1
+
R
r
)
α
)
{\displaystyle y=(R+r)\sin \alpha -r\sin \left(\left(1+{\frac {R}{r}}\right)\alpha \right)}
Siehe auch Epizykloide
c
=
r
⇒
{\displaystyle c=r\Rightarrow }
c
<
r
⇒
{\displaystyle c<r\Rightarrow }
c
>
r
⇒
{\displaystyle c>r\Rightarrow }
Epizykloiden sind genau dann geschlossene Kurven, wenn das Längenverhältnis
q
=
R
r
{\displaystyle q={\frac {R}{r}}}
Epizykloide#Geschlossenheit
Zwecks Herleitung siehe vorerst Epizykloide#Länge
Zwecks Herleitung siehe vorerst Epizykloide#Flächeninhalt
Eine Kreisscheibe 1 rollt innen auf einer anderen Kreisscheibe 2 ab. Ein auf der Kreisscheibe 1 festgelegter Punkt beschreibt dann eine Hypozykloide.
Parametergleichung der gewöhnlichen Hypozykloide:
x
=
(
R
−
r
)
cos
α
+
r
cos
(
(
R
r
−
1
)
α
)
{\displaystyle x=(R-r)\cos \alpha +r\cos(({\frac {R}{r}}-1)\alpha )}
y
=
(
R
−
r
)
sin
α
−
r
sin
(
(
R
r
−
1
)
α
)
{\displaystyle y=(R-r)\sin \alpha -r\sin(({\frac {R}{r}}-1)\alpha )}
Siehe auch Hypozykloide
Übung: Leiten Sie die Parametergleichung der gewöhnlichen Hypozykloide her.
c
=
r
⇒
{\displaystyle c=r\Rightarrow }
c
<
r
⇒
{\displaystyle c<r\Rightarrow }
c
>
r
⇒
{\displaystyle c>r\Rightarrow }
Hypozykloiden sind genau dann geschlossene Kurven, wenn das Längenverhältnis
q
=
R
r
{\displaystyle q={\frac {R}{r}}}
Hypozykloide#Geschlossenheit
Wenn
r
=
R
=
c
{\displaystyle r=R=c}
Kardioide
P
1
P
→
⋅
P
2
P
→
=
c
2
{\displaystyle {\overrightarrow {P_{1}P}}\cdot {\overrightarrow {P_{2}P}}=c^{2}}
(
x
2
+
y
2
)
2
−
2
a
2
(
x
2
−
y
2
)
=
c
4
−
a
4
;
a
,
c
∈
R
0
+
{\displaystyle (x^{2}+y^{2})^{2}-2a^{2}(x^{2}-y^{2})=c^{4}-a^{4};\quad a,c\in \mathbb {R} _{0}^{+}\quad }
P
1
=
(
a
,
0
)
{\displaystyle P_{1}=(a,0)}
P
2
=
(
−
a
,
0
)
{\displaystyle P_{2}=(-a,0)}
Siehe diesbezüglich auch Cassinische Kurve
F
1
P
→
⋅
F
2
P
→
=
a
2
{\displaystyle {\overrightarrow {F_{1}P}}\cdot {\overrightarrow {F_{2}P}}=a^{2}}
F
1
F
2
¯
=
2
a
{\displaystyle {\overline {F_{1}F_{2}}}=2a}
Parametergleichung:
x
=
a
2
cos
(
t
)
sin
2
(
t
)
+
1
{\displaystyle x={\frac {a{\sqrt {2}}\cos(t)}{\sin ^{2}(t)+1}}}
y
=
a
2
cos
(
t
)
sin
(
t
)
sin
2
(
t
)
+
1
{\displaystyle y={\frac {a{\sqrt {2}}\cos(t)\sin(t)}{\sin ^{2}(t)+1}}}
mit
0
≤
t
<
2
π
{\displaystyle 0\leq t<2\pi }
Kartesische Koordinaten:
(
x
2
+
y
2
)
2
−
2
a
2
(
x
2
−
y
2
)
=
0
{\displaystyle \left(x^{2}+y^{2}\right)^{2}-2a^{2}\left(x^{2}-y^{2}\right)=0}
y
=
±
a
4
x
2
+
a
2
−
x
2
−
a
2
{\displaystyle y=\pm {\sqrt {a{\sqrt {4x^{2}+a^{2}}}-x^{2}-a^{2}}}}
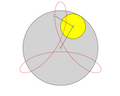
Siehe auch Lemniskate Lemniskate von Bernoulli
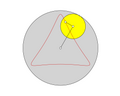
Konstruktion (Quelle: Versiera der Agnesi
...Beginnend mit einem festen Kreis wird ein Punkt O auf dem Kreis gewählt. Für jeden anderen Punkt A auf dem Kreis wird die Sekante OA gezeichnet. Der Punkt M ist diametrisch gegenüberliegend zu O. Die Linie OA schneidet die Tangente in M am Punkt N. Die Linie parallel zu OM durch N und die Linie rechtwinklig zu OM durch A schneiden sich in P. Wird der Punkt A geändert, so ist der Weg von P die Versiera der Agnesi...
Kartesische Koordinaten:
(
x
2
+
a
2
)
y
−
a
3
=
0
{\displaystyle (x^{2}+a^{2})y-a^{3}=0}
Parameterform:
x
=
a
t
{\displaystyle x=at}
y
=
a
t
2
+
1
{\displaystyle y={\frac {a}{t^{2}+1}}}
Parameterdarstellung:
x
=
a
sin
(
b
t
)
sin
(
t
)
{\displaystyle x=a\sin(bt)\sin(t)}
y
=
a
sin
(
b
t
)
cos
(
t
)
{\displaystyle y=a\sin(bt)\cos(t)}
Siehe z.B. [1] und Burg, Haf, Wille, Meister: Vektoranalysis; 2. Aufl., Springer, 2012, Seite 68f .
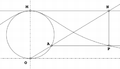
Das kartesische Blatt sei definiert durch die Gleichung
x
3
+
y
3
−
3
a
x
y
=
0
{\displaystyle x^{3}+y^{3}-3axy=0}
Parameterdarstellung:
x
=
3
a
t
1
+
t
3
{\displaystyle x={\frac {3at}{1+t^{3}}}}
y
=
3
a
t
2
1
+
t
3
{\displaystyle y={\frac {3at^{2}}{1+t^{3}}}}
Siehe auch Kartesisches Blatt
Parametergleichung:
x
=
2
a
t
2
1
+
t
2
{\displaystyle x={\frac {2at^{2}}{1+t^{2}}}}
y
=
2
a
t
3
1
+
t
2
{\displaystyle y={\frac {2at^{3}}{1+t^{2}}}}
Kartesische Koordinaten:
−
y
2
(
2
a
−
x
)
+
x
3
=
0
{\displaystyle -y^{2}(2a-x)+x^{3}=0}
Siehe auch Zissoide des Diokles
Parameterdarstellung:
x
=
a
(
t
2
−
1
)
1
+
t
2
{\displaystyle x={\frac {a(t^{2}-1)}{1+t^{2}}}}
y
=
a
t
(
t
2
−
1
)
1
+
t
2
{\displaystyle y={\frac {at(t^{2}-1)}{1+t^{2}}}}
Kartesische Koordinaten:
(
a
+
x
)
x
2
−
(
a
−
x
)
y
2
=
0
{\displaystyle (a+x)x^{2}-(a-x)y^{2}=0}
Siehe auch Strophoide
Archimedes von Syrakus (um 287 v. Chr. - 212 v. Chr.) griechischer Mathematiker, Physiker, Ingenieur
Anwendung: Schallplatte
Anwendung: Lakritz-Schnecken
Parameterdarstellung:
x
=
a
t
cos
t
{\displaystyle x=at\cos t}
y
=
a
t
sin
t
{\displaystyle y=at\sin t}
Polardarstellung:
r
=
a
⋅
φ
{\displaystyle r=a\cdot \varphi }
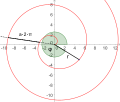
Siehe auch Archimedische Spirale
Polarkoordinaten:
r
(
φ
)
=
a
e
k
φ
{\displaystyle r(\varphi )=ae^{k\varphi }}
Parameterdarstellung:
x
(
φ
)
=
r
(
φ
)
cos
φ
=
a
e
k
φ
cos
φ
{\displaystyle x(\varphi )=r(\varphi )\cos {\varphi }=ae^{k\varphi }\cos {\varphi }}
y
(
φ
)
=
r
(
φ
)
sin
φ
=
a
e
k
φ
sin
φ
{\displaystyle y(\varphi )=r(\varphi )\sin {\varphi }=ae^{k\varphi }\sin {\varphi }}
Die logarithmische Spirale kommt in der Natur oftmals vor:
Siehe auch Logarithmische Spirale
Parameterdarstellung:
x
=
a
cos
φ
φ
{\displaystyle x=a{\frac {\cos \varphi }{\varphi }}}
y
=
a
sin
φ
φ
{\displaystyle y=a{\frac {\sin \varphi }{\varphi }}}
Sieh auch Hyperbolische Spirale
Die Klothoide wird auch Cornu-Spirale genannt.
Siehe auch Klothoide
Parameterdarstellung:
x
=
a
(
cos
t
)
2
+
b
cos
t
{\displaystyle x=a(\cos t)^{2}+b\cos t}
y
=
a
cos
t
sin
t
+
b
sin
t
{\displaystyle y=a\cos t\sin t+b\sin t}
Kartesische Koordinaten:
(
x
2
+
y
2
−
a
x
)
2
−
b
2
(
x
2
+
y
2
)
=
0
{\displaystyle (x^{2}+y^{2}-ax)^{2}-b^{2}(x^{2}+y^{2})\,=\,0}
Polarkoordinaten:
r
=
a
cos
φ
+
b
{\displaystyle r=a\cos \varphi +b}
Ein Sonderfall der pascalschen Schnecke ist die Kardioide.
Siehe auch Pascalsche Schnecke
y
=
a
cosh
x
a
{\displaystyle y=a\cosh {\frac {x}{a}}}
Die Katenoide ist die Evolute der Traktrix (Quelle: Bronstein: Taschenbuch der Mathematik; 7. Aufl., Harri Deutsch, 2008, Seite 108 ). Katenoide (Kettenlinien) werden häufig in der Architektur oder im Bauwesen verwendet. Aber auch in der Natur treten sie auf:
Siehe auch Kettenlinie (Mathematik
y
=
±
d
⋅
ln
|
d
+
d
2
−
x
2
x
|
⏟
=
arcosh
d
x
∓
d
2
−
x
2
{\displaystyle y=\pm \ d\cdot \underbrace {\ln \left|{d+{\sqrt {d^{2}-x^{2}}} \over x}\right|} _{=\operatorname {arcosh} {\frac {d}{x}}}\mp {\sqrt {d^{2}-x^{2}}}}
Bedeutung hat die Traktrix (Schleppkurve) u.a. im Straßenbau und in der Fahrzeugtechnik.
Siehe auch Traktrix
x
=
A
x
sin
(
ω
1
t
+
ϕ
1
)
{\displaystyle x=A_{x}\sin(\omega _{1}t+\phi _{1})}
y
=
A
y
sin
(
ω
2
t
+
ϕ
2
)
{\displaystyle y=A_{y}\sin(\omega _{2}t+\phi _{2})}
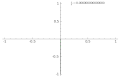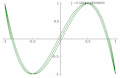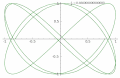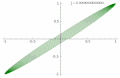
Lissajous-Figuren sind dann periodisch (geschlossene Figur), wenn das Frequenzverhältnis
v
=
ω
1
ω
2
{\displaystyle v={\frac {\omega _{1}}{\omega _{2}}}}
Siehe auch Lissajous-Figur


















![{\displaystyle \int _{2\pi }^{0}{\dot {x}}y\mathrm {d} t=-ab\int _{2\pi }^{0}\sin ^{2}t\mathrm {d} t=-ab\left[{\frac {1}{2}}t-{\frac {1}{4}}\sin(2t)\right]_{2\pi }^{0}=ab\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cba9eaec71f7363a14e9fee0c35780218780c975)









































![{\displaystyle L=2r\int _{0}^{2\pi }\sin {\frac {t}{2}}\mathrm {d} t\underbrace {=} _{\text{z.B. durch Substitution}}-4r\cos {\frac {t}{2}}|_{0}^{2\pi }=-4r[\underbrace {cos\pi } _{-1}-\underbrace {\cos 0} _{1}]=8r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfccf193a709262cfd104dfc550295bdb341ed89)
![{\displaystyle {\begin{aligned}A=-\int _{0}^{2\pi }{\dot {y}}x\mathrm {d} t=-\int _{0}^{2\pi }c\sin t(rt-c\sin t)\mathrm {d} t=-rc\int _{0}^{2\pi }t\sin t\mathrm {d} t+c^{2}\int _{0}^{2\pi }\sin ^{2}t\mathrm {d} t=\\-rc[\sin t-t\cos t]_{0}^{2\pi }+c^{2}[{\frac {1}{2}}t-{\frac {1}{4}}\sin(2t)]_{0}^{2\pi }=2rc\pi +c^{2}\pi =\pi (2rc+c^{2})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a92e02db5887ed4ee8ca5bfe75121a2a04c16c4)