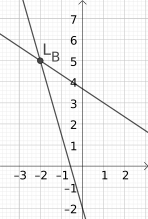MathemaTriX ⋅ Theorie. Klasse 5
| ||||||||||||||||||
|
Inhalt
Ein-Aus- klappen |
| AUFGABEN | |
|
|
Vorgabe des Ministeriums
[Bearbeiten]Zahlen und Rechengesetze
[Bearbeiten]- Reflektieren über das Erweitern von Zahlenmengen an Hand von natürlichen, ganzen, rationalen und irrationalen Zahlen
- Darstellen von Zahlen im dekadischen und in einem nicht-dekadischen Zahlensystem-
- Verwenden von Zehnerpotenzen zum Erfassen von sehr kleinen und sehr großen Zahlen in anwendungsorientierten Bereichen
- bewusstes und sinnvolles Umgehen mit exakten Werten und Näherungswerten
- Aufstellen und Interpretieren von Termen und Formeln, Begründen von Umformungsschritten durch Rechengesetze
- Arbeiten mit Primzahlen und Teilern, Untersuchen von Teilbarkeitsfragen
Gleichungen und Gleichungssysteme
[Bearbeiten]- Lösen von linearen und quadratischen Gleichungen in einer Variablen
- Lösen von linearen Gleichungssystemen in zwei Variablen, Untersuchen der Lösbarkeit dieser Gleichungssysteme, geometrische Interpretation
- Anwenden der oben genannten Gleichungen und Gleichungssysteme auf inner- und außermathematische Probleme
Funktionen
[Bearbeiten]- Beschreiben von Abhängigkeiten, die durch reelle Funktionen in einer Variablen erfassbar sind (mittels Termen, Tabellen und Graphen), Reflektieren über den Modellcharakter von Funktionen
- Beschreiben und Untersuchen von linearen und einfachen nichtlinearen Funktionen (zB a/x, a/x2, ax2+bx+c, abschnittweise definierte Funktionen)
- Untersuchen von Formeln im Hinblick auf funktionale Aspekte, Beschreiben von direkten und indirekten Proportionalitäten mit Hilfe von Funktionen
- Arbeiten mit Funktionen in anwendungsorientierten Bereichen
Trigonometrie
[Bearbeiten]- Definieren von sin α, cos α, tan α für 0° ≤α≤ 360°
- Durchführen von Berechnungen an rechtwinkligen und allgemeinen Dreiecken, an Figuren und Körpern (auch mittels Sinus- und Kosinussatz)
- Kennenlernen von Polarkoordinaten
Vektoren und analytische Geometrie der Ebene
[Bearbeiten]- Addieren von Vektoren und Multiplizieren von Vektoren mit reellen Zahlen, geometrisches Veranschaulichen dieser Rechenoperationen
- Ermitteln von Einheitsvektoren und Normalvektoren
- Arbeiten mit dem skalaren Produkt, Ermitteln des Winkels zweier Vektoren
- Beschreiben von Geraden durch Parameterdarstellungen und durch Gleichungen, Schneiden von Geraden
- Lösen von geometrischen Aufgaben, gegebenenfalls unter Einbeziehung der Elementargeometrie
Grundrechnungen
[Bearbeiten]Punktrechnungen mit 10, 100, 1000 und so weiter
[Bearbeiten]- Wenn man eine Zahl mit 10, 100, 1000 und so weiter multipliziert, dann verschiebt sich das Komma der Zahl einfach nach rechts (die Zahl wird größer), so oft, wie es Nullen gibt:
- 3,45 · 10 = 34,5 (Mal 10; in 10 gibt es eine Null, Komma wird einmal nach rechts verschoben)
- 54 · 10000 = 54,0000 · 10000 = 540000 (Mal 10000; in 10000 gibt es vier Nullen, Komma wird 4 Mal nach rechts verschoben; Allerdings gibt es kein Komma am Ende der Zahl 54; man schreibt ein Komma am Ende der Zahl und dazu nach dem Komma so viele Nullen, wie man will, und schiebt dann das Komma)
- 0,008 · 100 = 0,8 (Mal 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach rechts verschoben)
- Wenn man eine Zahl mit 10, 100, 1000 und so weiter dividiert, dann verschiebt sich das Komma der Zahl einfach nach links (die Zahl wird kleiner), so oft, wie es Nullen gibt:
- 3,45:10 = 0,345 (Durch 10; in 10 gibt es eine Null, Komma wird einmal nach links verschoben; allerdings gibt es links vor 3,4 keine Null, man schreibt also links von der Zahl so viele Nullen, wie man will, und schiebt dann das Komma)
- 54:10000 = 0,0054 (Durch 10000; in 10000 gibt es 4 Nullen, Komma wird 4 Mal nach links verschoben; allerdings gibt es links vor 54 kein Komma, man schreibt also links von der Zahl ein Komma und so viele Nullen, wie man will, und schiebt dann das Komma)
- 0,008:100 = 0,00008 (Durch 10; in 10 gibt es eine Null, Komma wird 1 Mal nach links verschoben; allerdings muss man zuerst am Ende der Kommazahl weitere Nullen schreiben)
- 900000:100 = 9000,00 = 9000 (Durch 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach links verschoben; da es kein Komma am Ende der Zahl gibt, muss man erst das Komma schreiben)
Textaufgaben zu den Grundrechenarten
[Bearbeiten]| Rechenart | Ausgedrückt als | Symbol | Namen der Teile | Name des Ergebnisses |
|---|---|---|---|---|
| Addition | plus | + | ||
| (addieren, erhöhen) | Summand Summand | Summe | ||
| Subtraktion | minus | − | ||
| (subtrahieren, reduzieren, vermindern, abziehen) | Minuend Subtrahend | Differenz | ||
| Multiplikation | mal | ⋅ (×) | ||
| (multiplizieren, vervielfachen, -fach) | Faktor ⋅ Faktor | Produkt | ||
| Division | durch | : (÷, /) | ||
| (dividieren, teilen) | Dividend Divisor | Quotient | ||
Mit den Grundrechenarten kann man auch Textaufgaben bilden. Bei diesen Aufgaben ist in der Regel die Bedeutung der Wörter nicht so wichtig, wie der Aufbau des Satzes:
- Dividieren Sie die Differenz von 125 und 20 mit der Summe von 4 und 3.
Schauen wir mal, wie der Satz aufgebaut ist. Erst steht, dass man dividieren muss (also durch machen). Was muss man aber dividieren? Was steht nach dem Wort dividieren? Die Zahlen 125 und 20? NEIN! Nach dem Wort dividieren (durch machen) steht das Wort Differenz! Man muss also erst eine Differenz berechnen! Welche Differenz? Die Differenz von 125 und 20(was nach dem Wort Differenz steht)! Das steht ja auch da! Die Differenz (Minus) von 125 und 20 ist 125−20=105. Diese Differenz muss man durch irgendwas dividieren. Ist das durch 4, durch 3 oder doch was anderes? Doch was anderes! Die Differenz muss man mit der Summe (Plus machen) dividieren. Man muss also erst eine Summe berechnen, die Summe von 4 und 3 (was nach dem Wort Summe steht), 4+3=7. Man soll also die Differenz (105) durch die Summe (7) dividieren:
105:7=15. 15 ist also die Antwort zur Aufgabe!
Doppelbrüche
[Bearbeiten]
Bruchrechnungen und Vorrang
[Bearbeiten]
Man muss zuerst die Klammern machen:
- Erste Klammer
Hier haben wir nur eine Strichrechnung und zwar mit dem gleichen Nenner.
- Zweite Klammer
Hier müssen wir erst die Punktrechnung machen und dann die Strichrechnung.
Hier soll man erst kürzen.
Jetzt kann man in der Rechnung die Ergebnisse für die Klammern einsetzen:
Textaufgaben zu den Bruchrechnungen
[Bearbeiten]- In einem Staat mit 8,46 Millionen Einwohner trinkt jeder Einwohner durchschnittlich vier Neuntel Liter Milch täglich.
-
- Wie viel Liter werden dann täglich konsumiert?
- Der Gewinn für die Eigentümer ist 0,8¢/Liter Milch. Wie viel ist der tägliche Gewinn? Finden Sie ihn gerechtfertigt?
- Im einem anderen Staat gibt es 4 Supermarktketten. Zusammen gewinnen die Eigentümer 105000€ täglich. Eigentümer A bekommt zwei Fünftel des Gewinns, Eigentümer B ein Drittel und den Rest teilen die anderen zwei Eigentümer C und D. Wie viel gewinnt täglich jeder Eigentümer? Finden Sie den Gewinn gerechtfertigt?
Aufgabe a lässt sich leicht berechnen:
Da der Gewinn pro Liter 0,8¢ ist, soll man 0,8 mit 3,76 Mil. multiplizieren (dann hat man ¢) und dann durch 100 dividieren (dann hat man €):
Ob dieser Gewinn gerechtfertigt ist, soll jeder für sich entscheiden (die Eigentümer werden ihn sicherlich gerechtfertigt finden, sonst würden sie ihn nicht machen...).
Aufgabe b ist ebenfalls nicht besonders schwer:
Eigentümer A:
Eigentümer B:
Eigentümer C und D teilen den Rest:
Primfaktorzerlegung Anwendungen
[Bearbeiten]Kürzen mit Primfaktorzerlegung
[Bearbeiten]
Hier sieht man sofort, dass man sowohl den Zähler als auch den Nenner durch 5 teilen kann. Was ist aber, wenn man große Zahlen hat? In diesem Fall ist es besser, die PFZ der Zahlen erst durchzuführen:
| ? |
| 6664 | 2 |
| 3332 | 2 |
| 1666 | 2 |
| 833 | 7 |
| 119 | 7 |
| 17 | 17 |
| 1 |
| 8820 | 2 |
| 4410 | 2 |
| 2205 | 3 |
| 735 | 3 |
| 245 | 5 |
| 49 | 7 |
| 7 | 7 |
| 1 |
| Man schreibt Zähler und Nenner als Produkt von Primzahlen und kürzt den Bruch (also Primzahlen, die oben und unten vorkommen, werden gestrichen) |
Bruchstrichrechnungen mit Primfaktorzerlegung
[Bearbeiten]
Wir haben schon gesehen, wie man zwei Brüche addiert oder subtrahiert. Was ist es aber, wenn man mehrere Brüche hat? Man könnte selbstverständlich erst die zwei Brüche machen, das Ergebnis mit dem nächsten Bruch usw. Das kann lang dauern und Brüche mit sehr große Nennern als Ergebnis haben. Es gibt eine Methode, die schneller ist und die Primfaktorzerlegung (PFZ) benutzt. Schauen wir ein Beispiel an. In unserem Beispiel wandeln wir erst die gemischten Zahlen in „unechten“ Brüchen um:
Jetzt machen wir die PFZ der Nenner:
| 36 | 2 |
| 18 | 2 |
| 9 | 3 |
| 3 | 3 |
| 1 |
| 24 | 2 |
| 12 | 2 |
| 6 | 3 |
| 3 | 3 |
| 1 |
| 45 | 3 |
| 15 | 3 |
| 5 | 5 |
| 1 |
| 40 | 2 |
| 20 | 2 |
| 10 | 2 |
| 5 | 5 |
| 1 |
also:
| 36 = 2·2·3·3 |
| 24 = 2·2·2·3 |
| 45 = 3·3·5 |
| 40 = 2·2·2·5 |
Als nächstes sollen wir das sogenannte „kleinste gemeinsame Vielfache“ (kgV) bilden. Das geht so: Wir schauen welche Faktoren in den Nennern vorkommen. In unserem Fall sind es 2, 3 und 5. Dann schauen wir, wo jeder von diesen Faktoren am häufigsten vorkommt.
2 kommt in 36 zwei mal vor, in 24 drei mal vor, in 45 kein mal und in 40 wieder drei mal vor. Am häufigsten also kommt 2 drei mal vor (in 36 oder in 40, das spielt keine Rolle, wichtig ist, dass 2 am häufigsten in irgendeinem Nenner drei mal vorkommt). In diesem Fall müssen wir für das kgV die 2 drei mal benutzen.
3 kommt in 36 zwei mal vor, in 24 ein mal, in 45 zwei mal und 40 kein mal vor. Am häufigsten kommt 3 also zwei mal vor (in 36 oder in 45, wir benutzen also nur 36 oder nur 45, also die 3 zwei mal). In diesem Fall müssen wir für das kgV die 3 zwei mal benutzen.
5 kommt in 36 kein mal, in 24 auch kein mal, in 45 ein mal und 40 auch ein mal vor. Am häufigsten kommt 5 also ein mal vor (in 45 oder in 40, das spielt keine Rolle, wichtig ist, dass 5 am häufigsten in irgendeinem Nenner ein mal vorkommt). In diesem Fall müssen wir für das kgV die 5 ein mal benutzen.
Also die 2 kommt in kgV als drei mal Faktor vor, die 3 zwei mal und die 5 ein mal vor:
kgV=2·2·2·3·3·5=360
Für den nächsten Schritt gibt es verschiedene Wege, wir schreiben hier den Weg, den wir für den einfachsten halten. Unsere Rechnung nach dem ersten Schritt (gemischte Zahlen in unechten Brüchen umwandeln) ist jetzt:
Wir multiplizieren unser kgV jeweils mit dem Zähler und dividieren jeweils durch den Nenner für jeden Bruch. Die Ergebnisse schreiben wir in einem Zähler auf, mit den jeweiligen Strichrechnungen dazwischen. Im Nenner kommt das kgV (hier 360) vor. Also:
Für den ersten Bruch: 360⋅83:36=830
Für den zweiten Bruch: 360⋅85:24=1275
Für den dritten Bruch: 360⋅44:45=352
Für den vierten Bruch: 360⋅1:40=9
Diese vier Zahlen kommen im Zähler mit den jeweiligen Strichrechnungen dazwischen vor, im Nenner kommt das kgV vor. Im Zähler machen wir dann auch die Strichrechnungen:
In diesem Fall können wir den Bruch auch weiter kürzen (hier mit 6). Daher ist das Ergebnis:
Wiederholen wir das Ganze:
|
|
| ||||||||||||
Textaufgaben Primfaktorzerlegung
[Bearbeiten]Teilbarkeit
[Bearbeiten]Für die Teilbarkeit durch 11 gibt es eine Regel: wenn die Differenz der alternierenden Summen der Ziffern einer Zahl 0 oder durch 11 teilbar ist, dann ist die Zahl auch durch 11 teilbar. Beispiel: 981607. Man nimmt die Summe der ersten, der dritten und der fünften (alternierend) Ziffer 9+1+0= 10 und die Summe der zweiten, der vierten und der sechsten (alternierend) Ziffer 8+6+7=21. Die Differenz der beiden Summen ist 21-10=11, was durch 11 teilbar ist. Daher ist auch 981607 durch 11 teilbar!
Zahlendarstellungen
[Bearbeiten]Darstellungen einer Zahl im Dezimalssystem
[Bearbeiten]{{#lsth:Mathematrix: MA TER/ Theorie/ Zahlendarstellungen Mengentheorie und Aussagenlogik|Darstellungen einer Zahl im
Binäre Zahlen
[Bearbeiten]Weitere Zahlensysteme
[Bearbeiten]Runden
[Bearbeiten]Grundregeln des Rundens
[Bearbeiten]Das Quadrat von 7 ist 49 und daher ist die Wurzel von 49 gleich 7 (sie sind Gegenrechnungen). Was ist aber mit der Wurzel von 7? Wenn man die Rechnung mit einem einfacheren Taschenrechner macht, kommt das folgende Ergebnis vor:
2,6457513110645905905
Das bedeutet, dass das Quadrat von 2,6457513110645905905 (die Gegenrechnung) 7 sein sollte. Wenn man aber mit dem Taschenrechner die Rechnung macht:
2,6457513110645905905² = 2,6457513110645905905 · 2,6457513110645905905
kommt 6,99999999999999999999 als Ergebnis heraus, was zwar fast 7 ist, aber nicht genau 7.
Man spricht in diesem Fall vom Runden. Der Taschenrechner gibt beim Wurzelziehen ein Ergebnis an, das nicht genau ist. Das genaue Ergebnis hat unendlich viele Nachkommastellen. Es ist unmöglich die Wurzel von 7 mit einer Kommazahl ganz genau zu bestimmen. Die einzige Weise die Wurzel von 7 genau anzugeben, ist zu schreiben!
Wie genau das Ergebnis mit Kommastellen ist, hängt vom Taschenrechner ab. Jeder Taschenrechner kann eine bestimmte Anzahl von Nachkommastellen berechnen. Die Wurzel aus 7 mit einer Kommazahl genau anzugeben ist aber nicht möglich.
Der Taschenrechner gibt ein Ergebnis an, das so nah wie möglich zum tatsächlichen Wert von ist und so viele Nachkommastellen hat, wie der Taschenrechner berechnen kann. In der Anzeige des Taschenrechners stehen sogar oft weniger Stellen (wieder gerundet) als die Stellen, die der Taschenrechner berechnen kann[1].
Das Runden ist in solchen Fällen unvermeidbar und oft notwendig und sinnvoll. Stellen wir uns vor, dass ein Produkt 6€ kostet. In einer Sonderaktion wird allerdings ein Rabatt 17% gewährt. In diesem Fall ist der Preis nach dem Rabatt:
6 ⋅ 0,83 = 4,938€
Hier muss man wieder runden. Die Münze mit dem kleinsten Wert ist 1¢ (0,01€). So was wie 0,008€ kann man nicht in Bar bezahlen. Man kann auch nicht genau 4.938€ bezahlen. Man muss auf zwei Nachkommastellen runden:
4,938€ ≈ 4,94€
Warum haben wir hier 4,94 und nicht 4,93 geschrieben?
4,938 liegt näher bei 4,94 als bei 4,93.
Wenn man rundet, rundet man auf (also eins nach oben), wenn die nächste Ziffer 5 oder mehr ist. Man rundet ab (also die Ziffer bleibt die gleiche), wenn die nächste Ziffer weniger als 5 ist:
5,6873729 ≈ 5,69 5,6873729 ≈ 5,687373
5,6873729 ≈ 5,68737 5,6873729 ≈ 5,687 8,785 ≈ 8,79
Im letzten Beispiel sehen wir, dass aufgerundet wird, wenn die nächste Ziffer 5 ist. 8,785 rundet man auf 8,79. Die nächste Ziffer von ist 5, daher wird aufgerundet. Diese Art vom Runden von 5 wird „kaufmännische“ Rundung genannt und wird in der Schule benutzt. Dieser Art der Rundung von 5 kann allerdings zu Probleme führen, besonders in der Statistik. Daher gibt es auch andere Regeln, wie man rundet, wenn die nächste Stelle eine einzige 5 ist.[2]
Wie viele Nachkommastellen muss man schreiben? Das ist vom Problem abhängig.
Die Ziffern ohne die Nullen zu Beginn oder am Ende der Zahl nennt man gültige Ziffern.
Es kann sein, dass bei einer Aufgabe festgelegt wird, auf wie viele Stellen gerundet wird:
Aufgabe: Runden auf drei (gültige) Stellen (oder in diesem Beispiel auf zwei Nachkommastellen)
5,6873729 ≈ 5,69
Aufgabe: Runden auf sieben Stellen (oder in diesem Beispiel auf sechs Nachkommastellen)
5,6873729 ≈ 5,687373
Aufgabe: Runden auf sechs Stellen (oder in diesem Beispiel auf fünf Nachkommastellen)
5,6873729 ≈ 5,68737
Aufgabe: Runden auf vier Stellen (oder in diesem Beispiel auf drei Nachkommastellen)
5,6873729 ≈ 5,687
Aufgabe: Runden auf zwei (gültige) Stellen[3] (oder in diesem Beispiel auf vier Nachkommastellen)
0,002356 ≈ 0,0024
Wenn es keine Angabe über die gültigen Ziffern gibt, schreibt man nicht mehr als 5 oder 6 gültigen Ziffern insgesamt (also samt Ziffer vor dem Komma), beispielsweise:
895,76038≈895,760 0,007854309826≈0,00785 9874086973≈9874100000
In manchen Fällen sollte es von der Aufgabe klar sein, wie vielen gültige Stellen zu erwarten sind. Ein solchen Beispiel haben wir schon mit dem € gesehen.
Ein anderes Beispiel ist, wenn man ein Messband benutzt, um einen Abstand zu messen. Ein Messband kann nur bis mm messen und nichts kleineres. Wenn der gemessene Abstand 145cm ist und ihn in 7 teilt, kann das Ergebnis nur eine Nachkommastelle haben (mm).
Wenn man die Zeit mit einem elektronischen Stoppuhr misst, zeigt diese oft Nachkkommastellen nach der Sekunde, z.B. 6,463s. Das ist wieder völlig daneben, da die Reaktionszeit des Menschen mehr als 0,1s ist. Man kann also mit einer Stoppuhr, die mit der Hand betrieben wird, nicht genauer als eine Nachkommastelle nach der Sekunde messen. Die restlichen Nachkommastellen führen zum falschen Eindruck, dass man doch so genau (mit drei Nachkommastellen) messen kann.
Hier kann man auch erklären: Eine Zahl ändert sich nicht, wenn man eine oder mehrere Nullen vor der ersten Ziffer oder nach der letzten Nachkommastelle hinzufügt:
7,34 = 007,34 = 7,340 = 7,34000 = 000007,34000000
8888 = 8888,0000 = 0008888
- ↑ Ferner rechnet ein Taschenrechner auch anders als ein typischer Heimcomputer oder ein Notebook. So kann sich zwischen derartigen Geräten ebenfalls ein Unterschied ergeben. Zudem kann es bei solchen Geräten Optionen geben, selbst festzulegen, auf wie viele Stellen ein Ergebnis berechnet werden soll.
- ↑
Bei der sogenannten kaufmännischen Rundung wird auch bei 5 aufgerundet, was insbesondere bei Verkaufsgeschäften mit kleinen Beträgen dem Händler zugute kommt, wenn dieser viele ähnliche Geschäfte macht, daher vermutlich auch der Name.
Um das zu verstehen, stelle man sich viele zufällige Zahlen vor, die gerundet werden sollen. Einmal wird die Summe aller Zahlen vor der Rundung berechnet, nennen wir diese Summe V (vor der Rundung). Anschließend wird die Summe aller Zahlen nach der Rundung berechnet, nennen wir diese Summe N (nach der Rundung).
Man wird feststellen, dass N größer oder gleich V sein wird, was daran liegt, dass bei dieser Methode bei 5 immer aufgerundet wird.
Um das zu vermeiden, gibt es ein besseres Rundungsverfahren, bei dem es zwei Möglichkeiten gibt. Im Falle von 5 wird bei der einen Möglichkeit immer so gerundet, dass die letzte Ziffer gerade ist. Bei der anderen Möglichkeit wird bei 5 immer so gerundet, dass die letzte Ziffer ungerade ist. Man entscheidet sich bei einer Aufgabe der Rundung vieler Zahlen anfangs einmalig für eine der beiden Möglichkeiten und bleibt daraufhin dabei.
Bildet man wieder die Summenprobe, wird man feststellen, dass es Zufall ist, ob V oder N größer ist oder beide sogar gleich sind.
Man sagt: Das Verfahren ergibt keine systematischen Abweichungen.
Beispiel zur Rundung hin zur geraden Ziffer:
8,775 ergibt auf drei Stellen gerundet 8,78
8,765 ergibt auf drei Stellen gerundet 8,76
8,755 ergibt auf drei Stellen gerundet 8,76
0,125 ergibt auf zwei Stellen gerundet 0,12
0,135 ergibt auf zwei Stellen gerundet 0,14
0,145 ergibt auf zwei Stellen gerundet 0,14
Entsprechend zur Rundung hin zu ungeraden Ziffern:
8,775 ergibt auf drei Stellen gerundet 8,77
8,765 ergibt auf drei Stellen gerundet 8,77
8,755 ergibt auf drei Stellen gerundet 8,75
0,125 ergibt auf zwei Stellen gerundet 0,13
0,135 ergibt auf zwei Stellen gerundet 0,13
0,145 ergibt auf zwei Stellen gerundet 0,15
Welches Rundungsverfahren anzuwenden ist, hängt davon ab, in welchem Zusammenhang gerechnet wird (kaufmännisch, wissenschaftlich, statistisch). - ↑ (0 zählt hier am Anfang der Zahl bei der Anzahl gültiger Stellen nicht mit)
Aufrunden von 9
[Bearbeiten]Wenn die Ziffer, die gerundet werden muss, 9 ist, gibt es beim Aufrunden eine gewisse Schwierigkeit. Die Ziffer sollte um 1 erhöht werden, es gibt aber keine Ziffer, die mehr als 9 ist. In diesem Fall wird wie bei der Division, also auch mit der vorherigen Ziffer gearbeitet. Runden wir folgende Beispiele auf drei gültigen Stellen:
- 8,695408
Wir wollen hier drei Stellen benutzen, die letzte Stelle ist 9. Nach der 9 folgt 5, wie müssen also aufrunden. 9 muss um 1 erhöht werden. Das geht nicht. Dann nimmt man zwei Ziffern (also hier die Ziffern nach dem Komma 69) und erhöht sie um 1 (69 wird zu 70). Also:
8,695408 ≈ 8,70
- 0,039995
Wir wollen wieder drei Stellen benutzen, die letzte Stelle ist 9. Nach der 9 folgt 9, wie müssen also aufrunden. 9 muss um 1 erhöht werden. Das geht nicht. Dann nimmt man zwei Ziffern (also hier die Ziffern 99) und versucht sie um 1 zu erhöhen. Das geht auch nicht, 99 ist die größte zweistellige Zahl. In diesem Fall nehmen alle drei Stellen (399) und erhöhen wir sie um 1:
0,039995≈0,0400
Die zwei Nullen nach dem 4 müssen geschrieben werden, um zu zeigen, dass es auf drei gültigen Stellen gerundet wurde.
- 999,73
In diesem Beispiel muss man wieder alle drei Stellen benutzen, das Runden findet aber doch davor statt!
999,73≈1000
Vorsilben und Gleitkommadarstellung
[Bearbeiten]Vorsilben
[Bearbeiten](auch: Vorsätze oder Präfixe: aus der Wikipedia Seite leicht verändert)
SI-Präfixe sind die für die Verwendung im Internationalen Einheitensystem (SI) (siehe Erklärung) definierte Dezimal-Präfixe. Sie basieren auf Zehnerpotenzen mit ganzzahligen Exponenten. Man unterscheidet zwischen dem Namen des Präfix und seinem Symbol. Die Symbole sind international einheitlich. Die Namen unterscheiden sich je nach Sprache. Die folgende Tabelle ist nicht vollständig, beinhaltet aber die in der Schulphysik meistbenutzten Vorsilben. Für eine vollständige Tabelle kann man die entsprechende Wikipedia Seite besuchen.
| Symbol | Name | Ursprung | Wert | ||
|---|---|---|---|---|---|
| T | Tera | gr. τέρας téras = Ungeheuer / gr. τετράκις tetrákis = viermal |
1012 | 1.000.000.000.000 | Billion |
| G | Giga | gr. γίγας gígas = Riese | 109 | 1.000.000.000 | Milliarde |
| M | Mega | gr. μέγα méga = groß | 106 | 1.000.000 | Million |
| k | Kilo | gr. χίλιοι chílioi = tausend | 103 | 1.000 | Tausend |
| h | Hekto | gr. ἑκατόν hekatón = hundert | 102 | 100 | Hundert |
| da | Deka | gr. δέκα déka = zehn | 101 | 10 | Zehn |
| — | — | — | 100 | 1 | Eins |
| d | Dezi | gr. δέκατος dékatos daraus lat. decimus = zehnter | 10−1 | 0,1 | Zehntel |
| c | Zenti | gr. ἑκατοστός hekatostós daraus lat. centesimus = hundertster | 10−2 | 0,01 | Hundertstel |
| m | Milli | lat. millesimus = tausendster | 10−3 | 0,001 | Tausendstel |
| µ | Mikro | gr. μικρός mikrós = klein | 10−6 | 0,000 001 | Millionstel |
| n | Nano | gr. νάνος nános = "Zwerg" | 10−9 | 0,000 000 001 | Milliardstel |
| p | Piko | ital. piccolo = klein | 10−12 | 0,000 000 000 001 | Billionstel |
Die Zeichen für Teile einer Einheit werden als Kleinbuchstaben geschrieben, während die meisten Zeichen für Vielfache einer Einheit als Großbuchstaben geschrieben werden. Ausnahmen von dieser Systematik sind aus historischen Gründen die Zeichen für Deka (da), Hekto (h) und Kilo (k).
Gleitkommadarstellung
[Bearbeiten]Es gibt verschiedene Weisen die gleiche Zahl zu schreiben. 0,00065 beispielsweise kann man auch als oder als oder als 650 · 10-6 usw. schreiben. Die normierte Gleitkommadarstellung ist die Darstellung, in der eine Zahl zwischen 1 und 9 vor dem Komma steht und möglicherweise Nachkommastellen und das ganze mit einer Zehnerpotenz multipliziert wird. Unseres Beispiel in Gleitkommadarstellung sieht so aus: 6,5 · 10-4. Es gilt also:
0,00065 = = 650 · 10-6 = 6,5 · 10-4
Was ganz rechts steht, ist die Gleitkommadarstellung der Zahl. Die Zahlen 0,22 · 104 und 22 · 102 sind nicht in Gleitkommadarstellung, weil die Zahl vor dem Komma nicht zwischen 1 und 9 ist. Die entsprechende Gleitkommadarstellung ist 2,2 · 103.
Zahl in Gleitkommadarstellung umwandeln
[Bearbeiten]Wie kann ich die Zahl 0,0072 in Gleitkommadarstellung umwandeln? 0,0072 ist eine Zahl kleiner als 1 (also null Komma irgendwas). Wenn ich sie in Gleitkommadarstellung schreiben will, wird die Potenz vom 10 negativ sein, und soviel, wie man das Komma nach rechts verschieben muss: 0,0072 = 7,2 · 10-3. Also, wenn eine Zahl kleiner also 1 ist (null Komma irgendwas) wird die Hochzahl der Potenz in der Gleitkommadarstellung negativ sein und genauso viel, wie ich das Komma nach rechts verschieben muss. Noch ein Beispiel: 0,00000054. Die Zahl ist kleiner als 1, also die Hochzahl in der Zehnerpotenz wird negativ sein. Wenn wir 5,4 schreiben, haben wir das Komma 7 mal nach rechts verschoben. Daher ist die Gleitkommadarstellung 5,4 · 10-7.
Nehmen wir jetzt eine Zahl größer als 1: 99500. Hier ist es leichter: das ist so viel wie 9,95 · 10000, also 9,95 · 104. Wir haben das Komma 4 mal nach links verschoben und die Hochzahl ist eindeutig positiv. Wenn also eine Zahl größer als 1 in Gleitkommadarstellung dargestellt wird, wird die Hochzahl in der Gleitkommadarstellung positiv sein und zwar so viel, wie man das Komma nach links verschoben hat. Noch ein Beispiel: 65100000000. Die Hochzahl wird eindeutig positiv sein (6,51 muss ich mit 10000000000 also 108 multiplizieren - und nicht 10-8 – damit das Ergebnis 65100000000 ist!) und so viel, wie ich das Komma verschieben muss, also die Gleitkommadarstellung ist 6,51 · 108.
Beispiel zur Gleitkommadarstellung
[Bearbeiten]0,008 μF = 800 · 10x MF
Es gibt unterschiedliche Weisen solch eine Aufgabe zu lösen. Eine davon ist, wenn man jede Seite in der normierten Gleitkommadarstellung umwandelt.
Die linke Seite der Gleichung (0,008 μF)
0,008 ist eine Zahl kleiner als 1 (also null Komma irgendwas). Wenn ich sie in Gleitkommadarstellung schreiben will, wird die Potenz vom 10 negativ sein, und soviel, wie man das Komma verschieben muss:
0,008 = 8 · 10-3
μ steht für mikro also für 10-6.
Daher ist die linke Seite in Gleitkommadarstellung:
| 0,008 | μ | F |
| ↓ | ↓ | |
| 8 · 10-3 · | 10-6 | F |
Die rechte Seite der Gleichung (800 · 10x MF)
800 ist eine Zahl größer als 1. Wenn ich sie in Gleitkommadarstellung schreiben will, wird die Potenz vom 10 positiv sein, und soviel, wie man das Komma verschieben muss:
800 = 8 · 102
M steht für Mega also für 106
Daher ist die rechte Seite in Gleitkommadarstellung:
| 800 · | 10x | M | F |
| ↓ | ↓ | ↓ | |
| 8 · 102 · | 10x | 106 | F |
Ergebnis
Die linke und die rechte Seite müssen gleich sein, also:
8 · 10-3 · 10-6 F = 8 · 102 · 10x · 106 F
und nach den Potenzregel:
8 · 10-3-6 F = 8 · 102+x+6 F
Der einzige Unterschied sind die Hochzahlen. Wir haben in beiden Seiten eine Multiplikation von Potenzen mit gleicher Basis (10), daher müssen die Summen der Hochzahlen auf beide Seiten gleich sein:
-3-6 = 2 + x + 6 -9=x+8 als x = -17
und daher:
0,008 μF = 800 ·10-17 MF
Zahlenmengen
[Bearbeiten]Einführung zu den Zahlenmengen
[Bearbeiten]Einfach gesagt ist eine Menge eine Sammlung von mehreren Sachen. Viele Bücher zusammen sind eine Menge von Büchern, viele Blumen zusammen sind eine Menge von Blumen, viele Ziegen und Schafen und Kühe zusammen sind eine Menge von Tieren. Man kann sogar von einer Menge sprechen auch, wenn man eine Sache hat (z. B. ein Buch) oder keine Sache (die leere Menge). Ein Bereich der Mathematik, die Mengentheorie, beschäftigt sich mit den Mengen. In dieser Theorie spricht man auch von Zahlenmengen.
Natürliche Zahlen
[Bearbeiten]Die einfachste Zahlenmenge ist die Menge der natürlichen Zahlen :
1, 2, 3, 4, 5, …
Die Menge der natürlichen Zahlen schreibt man mit . Null kann auch zur Menge der natürlichen Zahlen gehören. Wie man die Menge mit oder ohne Null schreibt, unterscheidet sich zwischen Sprachen und Kulturen.
Ganze Zahlen
[Bearbeiten]Die Menge der natürlichen Zahlen kann man mit den negativen Zahlen erweitern. Dann entsteht die Menge der ganzen Zahlen :
… −3, −2, −1, 0, 1, 2, 3, …
Alle natürliche Zahlen sind auch ganze Zahlen. Andererseits sind NUR die positive ganze Zahlen (oder die nicht negativen) auch natürliche Zahlen!
Rationale Zahlen
[Bearbeiten]Wenn man natürliche oder ganze Zahlen dividiert, bekommt man oft Zahlen mit Nachkommastellen:
Diese Zahl ist keine ganze (und daher auch keine natürliche) Zahl. Sie ist eine sogenannte rationale Zahl. Die Menge alle Zahlen, die man als Brüche von ganzen Zahlen schreiben kann, ist die Menge der rationalen Zahlen. Man soll aufpassen. 11 durch 7 (11:7) ist eine Division zwischen zwei ganzen Zahlen. Der Bruch hingegen ist eine Zahl (eine rationale Zahl), die gleich so viel ist, wie das Ergebnis (Quotient) der Division 11:7.
Wenn man zwei ganze Zahlen dividiert, kann man wieder eine ganze Zahle bekommen (wie z. B. 26:2=13) oder eine Zahl mit Nachkommastellen. Wenn das Ergebnis Nachkommastellen hat, dann ist sie keine ganze Zahl mehr.
Alle ganze Zahlen (und daher auch alle natürliche) sind auch rationale Zahlen (z. B. ). NUR die rationalen Zahlen OHNE Nachkommastellen sind auch ganze Zahlen.
Für die Zahlen mit Nachkommastellen gibt es zwei Möglichkeiten: sie können endlich viele Nachkommastellen haben (z. B. ) oder unendlich viele Nachkommastellen (wie ). Im letzten Fall gibt es in den Nachkommastellen eine Wiederholung von der gleichen Zahlenfolge:
Diese wiederholte Zahlenfolge (hier die Zahlenfolge ) nennt man Periode. Eine intuitive Erklärung für die Entstehung dieser Periode können wir bei der Division feststellen, wenn wir sie ohne Taschenrechner durchführen: Wenn nach der letzten Kommastelle unendlich lang Nullen geschrieben werden können und die Division dadurch weiter geführt werden kann, wird irgendwann als Rest genau die gleiche Zahl vorkommen und dadurch wird der Prozess wieder genauso wiederholt.
Die erweiterte Zahlenmenge (ganze Zahlen und dazu Zahlen mit endlich viele oder unendlich viele aber periodischen Nachkommastellen) nennt man Menge der rationalen Zahlen .
Reelle Zahlen
[Bearbeiten]Es gibt aber auch Zahlen, die zwar unendlich viele Nachkommastellen haben aber keine Periode. z. B. ist eine solche Zahl. Es gibt einen Beweis dafür, der zeigt, dass man NICHT als Bruch von zwei ganzen Zahlen ausdrücken kann. ist eine sogenannte irrationale Zahl. Die irrationale Zahlen (wie ) zusammen mit den rationalen (wie oder −6) bilden zusammen die Menge der reellen Zahlen .
ALLE rationale Zahlen sind auch reelle Zahlen. NICHT alle reelle Zahlen sind auch rationale Zahlen (z. B. ist eine Reelle aber keine Rationale Zahl).

Man kann also sagen: 5 ist eine natürliche aber auch eine ganze, eine rationale und eine reelle Zahl. ist eine rationale, eine reelle aber auch eine ganze Zahl (warum? Weil −14:7 = −2 ist und −2 eine ganze Zahl ist). Sie ist aber keine natürliche Zahl (weil −2 eine negative Zahl ist). ist nur eine reelle Zahl und keine rationale, ganze oder natürliche Zahl. ist eine reelle, aber auch eine rationale, eine ganze und eine natürliche Zahl (weil ist).
Eine Darstellung der Beziehungen zwischen den Mengen kann man im Bild sehen. Die reelle Zahlen beinhalten alle anderen Mengen, sie sind sozusagen die „größte“ Menge, die natürlichen Zahlen hingegen sind in allen anderen Mengen drinnen, beinhalten aber selber keine andere Menge (zumindest nicht in diesem Bild, also, wenn wir über diese 4 Mengen sprechen). Die natürliche Zahlen sind sozusagen die „kleinste“ Menge von diesen 4 Mengen.
Arbeiten mit Termen
[Bearbeiten]Term Definition
[Bearbeiten]Ein Term ist ein mathematischer Ausdruck. , , , , sind alles Terme, wobei aus mehreren Teiltermen besteht.
Potenzen
[Bearbeiten]Potenz Definition
[Bearbeiten]Jeder Term der Form mn ist eine Potenz. Was unten steht (hier m) nennt man Basis, was oben rechts (hier n) Hochzahl.
Potenz Was bedeutet diese Schreibweise?
Wenn man 4+4+4 hat, kann man auch 3·4 schreiben: . Eine Multiplikation zeigt, wie oft man eine Zahl mit sich selbst addiert.
Wenn man 4·4·4 hat, dann kann man 4³ schreiben. Eine Potenzzahl (hier 4³) zeigt, wie oft (so oft, wie die Hochzahl, hier 3) man eine Zahl (die Basis, hier 4) mit sich selbst multipliziert.
Potenzen Erklärung
[Bearbeiten]Strichrechnungen unter Potenzzahlen
[Bearbeiten]Wir haben gelernt, dass eine Multiplikation uns zeigt, wie oft die gleiche Zahl innerhalb einer Summe vorkommt. Beispielsweise ist . Das bedeutet allerdings auch, dass ist, weil
Eine Potenzzahl zeigt, wie oft die gleiche Zahl innerhalb eines Produktes vorkommt. Beispielsweise: .
Was ist jetzt, wenn wir Potenzzahlen addieren (oder subtrahieren)?
Nehmen wir ein Beispiel: .
Bei 3a² und 7a² hat die Potenzzahl a² die gleiche Basis a und die gleiche Hochzahl 2. Diese Potenzen können zusammengerechnet werden:
Entsprechend können wir mit a⁴ arbeiten:
a² und a⁴ können wir hingegen nicht zusammenrechnen, da sie zwar die gleiche Basis a aber nicht die gleiche Hochzahl (2 bzw. 4) haben.
a² und b² können wir auch nicht zusammenrechnen, da sie zwar die gleiche Hochzahl 2 aber nicht die gleiche Basis (a bzw. b) haben.
Daher ist:
Warum ist es so? Wie schon erwähnt, können nur gleiche Summanden durch eine Multiplikation ersetzt werden:
Wenn wir 3⁴ und 3² anstatt 3 haben, sind die Summanden nicht gleich, da 3⁴=3·3·3·3=81 und 3²=3·3=9 ist:
Noch ein Beispiel:
Multiplikation von zwei Potenzen mit der gleichen Basis
[Bearbeiten]
Warum das so ist, ist leicht zu erklären:
Die Hochzahlen addiert man, auch wenn sie negativ sind:
Allgemein kann man daher folgern:
wobei n und m irgendwelche positive oder negative reelle Zahlen sein können. Für den Fall von natürlichen Hochzahlen können wir schreiben:
Division von zwei Potenzen mit der gleichen Basis
[Bearbeiten]
Warum das so ist, ist leicht zu erklären:
Die Hochzahlen subtrahiert man (oben minus unten), auch wenn sie negativ sind:
Da ein Bruch (fast) gleichbedeutend mit einer Division ist, kann man auch sagen, dass bei der Division von Potenzzahlen mit gleicher Basis das Ergebnis die gleiche Basis ist, mit einer Hochzahl, die die Differenz aus der Hochzahl des Dividends und der Hochzahl des Divisors ist. Allgemein kann man daher schreiben:
wobei n und m irgendwelche positive oder negative reelle Zahlen sein können.
Null als Hochzahl
[Bearbeiten]
und nach der Regel gilt auch:
Also ist gleichzeitig gleich 1 und gleich . Daher gilt:
Potenzen mit negativer Hochzahl
[Bearbeiten]
Nach der Regel gilt:
Also ist gleichzeitig und . Daher gilt:
und allgemein:
Es muss auch klar sein: x² ist nicht das Gleiche wie y² (kann ausnahmsweise sein, ist es in der Regel aber nicht!)! Wenn die Basis anders ist, kann man mit den Hochzahlen keine Strichrechnung machen, z.B.:
oder etwas Ähnliches. Man kann einfach diesen Ausdruck NICHT vereinfachen!
Potenz einer Potenzzahl
[Bearbeiten]
Warum das so ist, kann man wie im Folgenden erklären:
- Kurze Erklärung zum Schritt : . Hier haben wir die eben erklärte Multiplikationsregel benutzt: .
Die Hochzahlen multipliziert man, auch wenn sie negativ sind:
Allgemein kann man daher schreiben:
wobei n und m irgendwelche positive oder negative reelle Zahlen sein können.
Potenz eines Produktes oder eines Bruches
[Bearbeiten]Mit einem Beispiel kann auch dieser Zusammenhang schnell erklärtwerden:
und entsprechend für einen Bruch:
Es gilt also allgemein:
Weitere Beispiele:
{{#ifeq:Mathematrix: AT AHS/ Theorie/ Klasse 5|Mathematrix: AT PSA Theorie nach Thema/ Arbeiten mit Termen
|
|
Potenzen mit Bruchhochzahl
[Bearbeiten]
Versuchen wir jetzt diesen Zusammenhang zu erklären.
Im Kapitel über Kubikwurzel lernen wir, dass die Gegenrechnung einer Hochzahl die entsprechende Wurzel ist:
und allgemein:
Es gilt allgemein, dass wenn eine Rechnung und ihre Gegenrechnung verwendet werden, das Ergebnis der Anfangswert sein wird:
(Die Gegenrechnung von +6 ist −6)
(Die Gegenrechnung von ⋅5 ist ÷5)
(Die Gegenrechnung von Quadrat ist die Quadratwurzel)
und allgemein für die Gegenrechnung einer Wurzel, wie eben gezeigt:
Benutzten wir jetzt die eben gelernte Regel über Potenz einer Potenz. Wie sollen die Hochzahlen aussehen, damit das Ergebnis der Anfangswert ist?
da ist
Es soll also für die Hochzahlen und gelten:
und daher
Ersetzen wir dann durch im Ausdruck und vergleichen wir folgende zwei Ausdrücke:
Beide Ausdrücke sind gleich a und daher gleich zueinander. Damit die Ausdrücke gleich sind, muss die Basis in beiden Fällen gleich sein:
Allgemeiner gilt also:
und:
}}
Arbeiten mit Potenzen Die Rechenregel zusammengefasst
[Bearbeiten]Komplexe Beispiele mit Potenzzahlen
[Bearbeiten]|style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |- |style="padding: 0.5em; margin: 0.3em"| | |style="padding: 0.5em; margin: 0.3em"| |}
In diesem Absatz erklären wir anhand von Beispielen, wie wir die Rechenregeln der Potenzzahlen anwenden können.
Wenn wir im Ausdruck eine Wurzel haben, ist es unsere erste Aufgabe, diese Wurzel als Potenzzahl zu schreiben. Die Wurzelpotenz soll als Nenner eines Bruches in der entsprechenden Hochzahl geschrieben werden (oder im Nenner eines Bruches, wenn die entsprechende Hochzahl schon ein Bruch ist):
oder auf einmal:
In diesem Ausdruck haben wir keinen Bruch oder Produkt von Potenzzahlen. Es geht um die Potenz einer Potenz (einer weiteren Potenz) und daher müssen wir nach der entsprechenden Regel die Hochzahlen einfach multiplizieren:
oder einfacher:
Jetzt wenden wir einfach die Multiplikationsregel von Zahlen an (minus mal minus ist plus) und führen diese Multiplikation aus:
Hier brauchen wir nur den zweiten und dritten Schritt der vorherigen Aufgabe durchführen. Am Ende haben wir allerdings in die Gegenrichtung gearbeitet und den Nenner im Bruch als Wurzelpotenz in einer Wurzel geschrieben.
Dieses Beispiel sieht kompliziert aus. Das sollte uns nicht aus der Fassung bringen. Die Schritten bleiben doch die gleichen:
Erst schreiben wir die Wurzel als Potenzzahl, also die Wurzelpotenz als Nenner in der entsprechenden Hochzahl:
Hier haben wir allerdings auch die Klammer in der Klammer aufgelöst (der erster Ausdruck links auf der linken Seite), indem wir die Regel der Potenz einer Potenz angewandt haben (Hochzahlen multiplizieren):
Wir haben also ein Produkt aus Potenzen mit der gleichen Basis, wir sollen daher die Regel anwenden und die Hochzahlen addieren:
und am Ende die Regel für die Potenz einer Potenz anwenden, also die Hochzahlen multiplizieren:
Dieser Ausdruck sieht noch komplizierter aus, das sollte uns aber immer noch nicht aus der Fassung bringen. Wir sollen ganz gemütlich und ruhig die Regeln anwenden. Um die Lösung klarer zu machen, bearbeiten wir im Folgenden erst den Zähler und dann den Nenner.
Wie in den vorherigen Beispielen, haben wir hier erst die Wurzel als Potenz ausgedrückt, indem wir die Wurzelpotenz in den Nenner der Hochzahl geschrieben haben. Wir haben daher die Potenz einer Potenz und wir müssen die Hochzahlen multiplizieren:
In der Hochzahl haben wir eine Multiplikation von Brüchen und diese führen wir aus (indem wir kürzen): . Es gilt daher für den Zähler:
Zähler
Im Nenner haben wir einen Bruch von Potenzzahlen mit der gleichen Basis, wir müssen daher die Hochzahl oben minus die Hochzahl unten berechnen:
Nenner
Wir schreiben also jetzt zusammen den Zähler und den Nenner in einem Bruch, wie es dazu gehört. Wir haben dann einen Bruch von Potenzen mit der gleichen Basis, wir müssen also die Hochzahl oben minus die Hochzahl unten berechnen:
Terme Grundaufgaben
[Bearbeiten]Vereinfachen Sie!
3x²+5-7x⁵+11-4x²+3-11x⁵+7x²=?
Diesen Term kann man vereinfachen, indem man Gleiches mit Gleichem addiert bzw. subtrahiert:
Mit Rot sind alle Teilterme (Summanden), die x2 beinhalten, mit Blau alle Teilterme, die x5 beinhalten und mit Schwarz alle einfachen Zahlen markiert. Man summiert die entsprechenden Teilterme. x2 gibt es 3-4+7 also insgesamt 6 mal, x5 (mit Blau) -7-11 also -18 mal und die Zahlen summiert man auch, 5+11+3 ist 19. Das Gesamtergebnis kann man vereinfacht so schreiben:
6x² +19 -18x⁵
Klammer Auflösen
[Bearbeiten]Ziel des Ausmultiplizierens
[Bearbeiten]Lösen Sie die Klammern auf!
Ziel solcher Aufgaben ist, einen Ausdruck ohne Klammern zu schreiben, der gleichwertig zu diesem Ausdruck (mit Klammern) ist. Probieren wir zunächst einmal die Klammern einfach wegzulassen. Zuerst soll man etwas erklären:
Wenn zwischen zwei mathematischen Ausdrücken nichts (keine Rechenart) steht, ist ein "mal" gemeint (Multiplikation) (einzige Ausnahme sind hier die gemischten Zahlen)
Probieren wir jetzt in beiden Ausdrücken eine Zahl an der Stelle von x einzusetzen, beispielsweise 0:
Die beide Ausdrücke sind nicht gleich. Probieren wir es auch mit 1:
Wieder sind die Ausdrücke nicht gleich. Man sagt dann, dass ist, dass nicht gleich zu ist. Obwohl eine Zahl schon ausreichen könnte, stimmt das eigentlich für alle Zahlen, die man für einsetzen kann.
Probieren wir dann beide Summanden in der Klammer mit dem Ausdruck außerhalb der Klammer zu multiplizieren:
Egal mit welcher Zahl wir es jetzt ausprobieren, werden die beide Ausdrücke immer gleich sein! Beispielsweise mit :
Da das immer gilt, kann man schreiben:
Wir haben daher unser Ziel erreicht! Wir haben einen gleichwertigen Ausdruck ohne Klammern!
Klammern werden aufgelöst, indem jeder Summand in Klammern mit dem Ausdruck außerhalb der Klammer multipliziert wird.
Erklärung des Ausmultiplizierens
[Bearbeiten]Denken wir an eine Kiste die 2 Zitronen und 4 Birnen hat:
|
|
Nehmen wir an, dass wir diese Kiste 3 mal haben:
|
|
|
|
In diesem Fall haben wir 3 mal 2 also 6 Zitronen und 3 mal 4 also 12 Birnen.
Den Inhalt der Kiste müssen wir mit 3 multiplizieren und zwar muss jede verschiedene Sorte, die in der Kiste ist, mit 3 multipliziert werden.
Ein Klammer ist genau so wie eine Kiste:
Wir haben einfach statt Bilder für die Zitronen den Buchstabe z und für die Birnen den Buchstabe b benutzt.
Es spielt keine Rolle, ob außerhalb der Kiste eine Zahl oder ein Symbol steht:
Zwischen 2z und 4b steht ein Plus. Der Vorgang ist der gleiche bei Minus:
Auch wenn wir Minus haben, können wir die verschiedenen Sorten (hier 2z und 4b) Summanden nennen.
Beispiel:
Ausmultiplizieren mit einer oder zwei Klammer
[Bearbeiten]Aufgaben mit einer Klammer
[Bearbeiten]
Die Aufgabe hier ist, einen gleichwertigen Ausdruck ohne Klammern zu schreiben. Wie eben erklärt, multipliziert man dafür den Term außerhalb der Klammer ( ) mit jedem Summand in den Klammern (also erst mit , dann mit und dann mit ):
Der Ausdruck am Ende ist immer gleich mit dem Ausdruck am Anfang. Wir haben also die Klammer aufgelöst!
Aufgaben mit 2 Klammern
[Bearbeiten]
Die Aufgabe hier ist wieder, einen gleichwertigen Ausdruck ohne Klammern zu schreiben. Um das zu machen, multipliziert man jeden Summand der ersten Klammer mit jedem Summand der zweiten Klammer :
Zu bemerken ist, dass −8x²−15x² eine Strichrechnung zwischen Potenzen ist. Daher gelten hier die entsprechenden Regel der Strichrechnungen unter Potenzzahlen
Hier gilt die Multiplikationsregel der Vorzeichen: plus mal plus ist plus, plus mal minus ist minus, minus mal plus ist minus, minus mal minus ist plus. (Das Gleiche gilt bei durch)
+ · + = +
+ · − = −
− · + = −
− · − = +
Hier ist darauf zu achten, dass die Regel ausschließlich bei Punktrechnungen gilt (Multiplikation und Division). Hier ein paar Beispiele, die den Zusammenhang klar machen sollten:
5−6=−1
In diesem Fall haben wir eine Strichrechnung zwischen zwei Zahlen: 5 MINUS 6, was insgesamt MINUS 1 beträgt.
5·(−6)=−30
In diesem Fall haben wir eine Punktrechnung (mal) zwischen eine positive und eine negative Zahl, also hier gilt + · − = − und die Werte 5 und 6 müssen wir multiplizieren (5 mal 6 ist 30).
−20−4=−24
In diesem Fall haben wir eine Strichrechnung zwischen zwei Zahlen, wobei die erste Zahl negativ ist, also MINUS 20 MINUS 4, was insgesamt MINUS 24 beträgt.
−20 : (−4)=5
In diesem Fall haben wir eine Punktrechnung (durch) zwischen zwei negative Zahlen, also hier gilt − · − = + und die Werte 20 und 4 müssen wir dividieren (20 durch 4 ist 5).
5+6=11
In diesem Fall haben wir eine Strichrechnung zwischen zwei Zahlen: 5 PLUS 6, was insgesamt 11 beträgt.
5·6=30
In diesem Fall haben wir eine Punktrechnung (mal) zwischen zwei positive Zahlen, also hier gilt + · + = + und die Werte 5 und 6 müssen wir multiplizieren (5 mal 6 ist 30). Diese Berechnung ist gleichbedeutend mit (+5)·(+6)=30.
Die Berechnung 5−6=−1 ist gleichbedeutend mit 5+(−6)=−1. Hier haben wir zwar keine ausdrückliche Multiplikation, wir addieren allerdings eine negative Zahl. In solchen Fällen sollen wir schon die plus mal minus Regel anwenden, wir haben aber doch keine Multiplikation, also 5 wird NICHT mit 6 multipliziert. Die Regel gilt nur für die Vorzeichen. Daher gilt:
5+(+6)=11
5−(+6)=−1
5−(−6)=5+6=11
5+(−6)=−1
Es gilt auch: −5+6=1
Arbeiten mit negativen Zahlen
[Bearbeiten]Wir haben die Regeln für die Multiplikation mit Plus und Minus gesehen. Wie kann man diese Regeln mit Zahlen erklären?
Dass ist, ist trivial. ist und ist . ist daher gleichbedeutend wie und, wie Multiplikation definiert wird, ist das 15.
Dass ist, macht eben auch Sinn. Laut Definition der Multiplikation ist , wie man beim Arbeiten mit negativen Zahlen lernt.
Wenn man hat, ist die Erklärung ebenso leicht. In der Multiplikation spielt die Reihenfolge keine Rolle, daher ist .
Warum ist aber Minus mal Minus doch Plus?
Um das zu erklären, kann man folgende Rechnung betrachten:
Macht man nach der Regel erst die Rechnung in Klammern, ist das Ergebnis:
Wenn erst die Klammer aufgelöst wird, wie wir das vorher gelernt haben, dann ergibt sich Folgendes:
ist , wie wir eben gelernt haben.
Wenn Minus mal Minus Plus ist, dann ist und das Ganze ergibt:
Wenn Minus mal Minus Minus wäre, dann wäre und das Ganze ergäbe:
was ein falsches Ergebnis ist, da wir schon gesehen haben, dass das Ergebnis, wenn man erst die Rechnung in Klammern macht, ist. Ähnliche Ergebnisse bekommt man, egal welches Beispiel benutzt wird. Daher ist Minus mal Minus Plus.
Ähnliches gilt, wenn man nur Vorzeichen hat:
Herausheben
[Bearbeiten]- 6x⁷ – 14x² + 10x³=? Heben Sie heraus!
(das ist allerdings das gleiche Beispiel, wie in Klammer auflösen, nur in die Gegenrichtung).
Die kleinste Hochzahl von x ist 2. Jeder Summand hat daher ein x² drinnen. Außerdem kann man die Zahl in jedem Summand durch 2 teilen. Also jeder Summand hat daher eine 2 drinnen. 2x² ist daher das gemeinsame Element, es bleibt außerhalb der Klammer:
6x⁷ – 14x² + 10x³= 2x² · (3x⁵-7+5x)
Wie haben wir die Teilterme in der Klammer gefunden?
6x⁷ : 2x² = 3x⁵, 14x² : 2x² = 7, 10x³ : 2x² = 5x !
Bei den Hochzahlen wählt man die kleinste Hochzahl. Wenn eine Variable bei einem Summand nicht vorkommt, dann kann man sie nicht herausheben. Bei den Zahlen kann man erst die Primfaktorzerlegung durchführen und dann die gemeinsamen Faktoren herausheben:
- 45b⁴y²n⁷ – 30y⁵n⁹ – 75b⁸y⁸n⁸ + 105 b y n⁷ = ?
45b⁴y²n⁷ – 30y⁵n⁹ – 75b⁸y⁸n⁸ + 105 b y n⁷ = 3·3·5 b⁴y²n⁷ – 2·3·5 y⁵n⁹ – 3·5·5 b⁸y⁸n⁸ + 3·5·7 b y n⁷
Hier haben wir die PFZ gemacht. Überall kommt 3 und 5 zumindest einmal vor, b kommt im zweiten Summand nicht vor (daher kann man b nicht herausheben), die kleinste Hochzahl von y ist 1 (y=y¹) und von n 7. Man kann also „3“, „5“, „y“ und „n⁷“ herausheben:
3·5 y n⁷ · (...?...) = 15yn⁷ · (...?...)
Was bleibt jetzt in der Klammer? Wir dividieren jeden Teilterm (Summand) mit dem herausgehobenen Teilterm (15yn⁷):
| 45b⁴y²n⁷ : 15yn⁷ = 3b⁴y | 30y⁵n⁹ : 15yn⁷ = 2y⁴n² | |
| 75b⁸y⁸n⁸ : 15yn⁷ = 5b⁸y⁷n | 105 b y n⁷ : 15yn⁷ = 7b |
also:
45b⁴y²n⁷ – 30y⁵n⁹ – 75b⁸y⁸n⁸ + 105 b y n⁷ = 15yn⁷ ( 3b⁴y – 2y⁴n² – 5b⁸y⁷n+ 7b )
Umformen
[Bearbeiten]Umformen Grundwissen Gegenrechnungen
[Bearbeiten]Wie kann man diese Aufgabe in der mathematischen Sprache schreiben? Für das Gefragte (wie viele Äpfel) wird in Mathematik irgendein Symbol benutzt, als Stellvertreter für die noch unbekannte Zahl. In der Regel wird als Symbol ein Buchstabe verwendet und nicht allzu selten x.
Mit x sind also die Äpfel gemeint, die Vassili am Anfang hatte. Wir wissen noch nicht, wie viele sie waren, daher schreiben wir ein Symbol dafür, ein Buchstabe, also x.
Wenn Vassili drei Äpfel der Lisa gibt, dann hat er weniger Äpfel als zuvor, es geht um eine Subtraktion. Von den x Äpfeln am Anfang sind drei Äpfel zu subtrahieren. Dass dann noch fünf Äpfel bleiben, wird durch den folgenden mathematischen Ausdruck geschrieben:
x−3=5
Man kann für x verschiedene Zahlen ausprobieren, z.B. 2, 3, 7, 8 oder 9. So kann man schon feststellen, dass nur acht minus drei gleich fünf ist. „x“ muss also 8 sein, damit die Rechnung stimmt. Vassili hatte also 8 Äpfel am Anfang.
Die ganze Zeit ausprobieren ist allerdings nicht gerade geschickt. Besonders bei größeren Zahlen wird es sogar ziemlich schwer. Es gibt in der Mathematik einen geschickteren Weg, die Aufgabe zu lösen. Man benutzt die sogenannte Gegenrechnung. Bei allen Gleichungen gibt es zwei Teile, ein Teil links vom „=“ und ein Teil rechts vom „=“. Bringt man einen Term von einer Seite zur anderen, dann muss man die Gegenrechnung benutzen.
Die Gegenrechnung der Subtraktion ist die Addition und umgekehrt.
Wenn x−3=5 ist, dann kann man die 3 auf die andere Seite vom „=“ bringen und statt minus die Gegenrechnung (plus) benutzen:
x=5+3 also x=8
Bei der Aufgabe c+4452 = 341 bringt man 4452 auf die andere Seite und benutzt die Gegenrechnung von minus. Die Lösung ist daher:
c+4452 = 341 → c= 341−4452 → c = −4111
Die Gegenrechnung der Multiplikation ist die Division und umgekehrt.
3f=114
Zwischen 3 und f steht nichts.
Wenn in Mathematik zwischen zwei Ausdrucken (zum Beispiel einer Zahl und einem Symbol, einer Klammer und einer Zahl und so weiter) nichts steht, dann ist Multiplikation gemeint (einzige Ausnahme: die gemischten Zahlen).
Da zwischen 3 und f nichts steht, ist mal gemeint. f ist ein Symbol und steht für irgendeine Zahl. Die Aufgabe ist herauszufinden, wie viel f sein soll, damit die Rechnung stimmt. In diesem fall soll 3 auf die andere Seite gebracht und die Gegenrechnung von mal (also durch) benutzt werden:
3f=114 (nichts zwischen 3 und f, also mal gemeint):
3·f=114 (3 auf die andere Seite von „=“ bringen und Gegenrechnung, also hier Division, benutzen)
f=114:3 und daher
f = 38.
Man kann auch einen Bruch statt einer Division benutzen:
Entsprechend ist die Gegenrechnung der Division die Multiplikation:
also k:5 = 11 und daher k = 11 · 5
k = 55
Was ist aber die Gegenrechnung vom Quadrat?
Die Gegenrechnung von Quadrat ist die sogenannte „Wurzel“:
z² = 81 also z = und daher z=9
9 ist die Zahl, deren Quadrat 81 ist, daher ist die Wurzel von 81 gleich 9. Wenn wir in der Gleichung z² = 81 z durch 9 ersetzen, dann stimmt die Gleichung tatsächlich: 9² = 81
Selbstverständlich ist die Gegenrechnung der Wurzel das Quadrat.
= 13 also m = 13² und daher m=169
Obwohl es für das Niveau dieses Buches nicht absolut notwendig ist, können wir doch auf eine Tatsache aufmerksam machen: Die Gleichung z² = 81 hat noch eine Lösung, wenn z gleich −9 ist. Freilich stimmt die Gleichung (−9)² = 81. (−9)² bedeutet (−9)·(−9). Minus mal minus ist plus und daher:
(−9)² =(−9)·(−9)= + 9·9 = 81 also
(−9)² = 81
Umformen einfache Kombinationen
[Bearbeiten]5x − 7 = 3x + 11
Wir wählen die linke Seite als die Seite, in der die Teilterme (Summanden) mit der gesuchten Variable (x) sein werden. Wir haben zwei solchen Teilterme, 5x und 3x. 5x ist schon auf der linken Seite, wir müssen also noch 3x auf die andere Seite bringen. Vor 3x steht das Symbol „=“. Ist 3x jetzt positiv oder negativ? Wenn man b=4 schreibt, ist +4 oder −4 gemeint? Die Antwort ist +4. Daher auch hier, wenn nach dem Symbol „=“ kein plus oder minus steht, dann ist ein plus gemeint. Wenn man 5x − 7 = 3x + 11 schreibt, ist es das Gleiche wie + 5x − 7 = + 3x + 11. Wenn man den Term 3x auf die andere Seite bringt, muss man die Gegenrechnung benutzen, also Subtraktion (minus).
5x − 7 − 3x = 11
7 hat kein x neben sich, sie muss auch auf die rechte Seite gebracht werden, wieder mit der Gegenrechnung, also diesmal mit Addition (plus):
5x − 3x = 11 + 7
Das Ganze kann man in einem Schritt machen:
5x − 7 = 3x + 11
5x − 3x = 11 +7
2x = 18
(Hier haben wir einfach die Rechnungen gemacht: 5x-3x ist 2x und 11+7 ist 18).
Es bleibt noch, 2 auf die andere Seite zu bringen. Zwischen 2 und x steht nichts, daher ist eine Multiplikation gemeint. Die Gegenrechnung ist eine Division:
x = und daher x = 9
Man kann das ganze auch so erklären:
5x − 7 = 3x + 11
Man will, dass auf der rechten Seite 3x verschwindet. Das kann passieren, indem man 3x subtrahiert. Ein Gleichung aber ist wie eine Waage. Das Gleichungssymbol (=) teilt die Gleichung in zwei Teilen, links und rechts. Was auf der einen Seite passiert, muss auch auf der anderen stattfinden, damit das Gleichgewicht erhalten bleibt. Man benutzt folgende Schreibweise:
5x − 7 = 3x + 11 | −3x (Man schreibt am Rand, was auf beiden Seiten zu tun ist)
5x − 7 − 3x = 3x + 11 − 3x
2x − 7 = 11
Man will aber auf der linken Seite nur Teilterme (Summanden) mit x haben, deshalb muss die -7 dort verschwinden. Das geht, indem man 7 auf beiden Seiten addiert.
2x − 7 = 11 | +7
2x − 7 + 7 = 11 + 7
2x = 18
Jetzt bleibt nur die Division:
2x = 18 | :2
x = 18 : 2 (Man kann auch schreiben)
x = 9
Sofern mehrere Teilrechnungen oder Zwischenschritte im Kopf durchgeführt werden, wird zusammengefasst und kürzer notiert:
5x − 7 = 3x + 11 | −3x+7
2x = 18 | :2
x =
x = 9
Wenn die Variable innerhalb einer Klammer steht, ist der erste Schritt, die Klammer aufzulösen, sonst geht man wie vorher vor:
4y + 3 (7 − 5y) = 11 − 6y
4y + 21 − 15y = 11 − 6y | −21
4y − 15y = 11 − 6y −21 | +6y
4y − 15y + 6y = 11 − 21
− 5y = −10 | : (−5)
y=2
Wenn man y durch 2 in der Anfangsgleichung 4y + 3 (7 − 5y) = 11 − 6y ersetzt, stellt man fest, dass die Gleichung tatsächlich stimmt.
4y + 3 (7 − 5y) = 11 − 6y
4·2 + 3 (7 − 5·2) = 11 − 6·2
8 + 3 ·(−3) = 11 − 12
8 − 9 = − 1
In der Tat ist 2 der einziger Wert von y, für den die Gleichung wirklich stimmt. Die LeserInnen können andere Werte ausprobieren und feststellen, dass die Gleichung dann nicht mehr stimmt.
Komplexe Umformungen
[Bearbeiten]
Wenn hier m gefragt ist, ist es völlig irrelevant, wie kompliziert der Rest aussieht. In unserem Kopf sollen wir folgendes Bild haben:
Dieses Bild wird noch einfacher, wenn wir in unserem Kopf A1 und A5 als ein Box denken und entsprechend A2 und A3. Das geht, weil die ersten zwei Summanden sind, die auf die andere Seite gehen sollen, und die letzten zwei ein Produkt sind:
Wir brauchen die Fassung nicht verlieren. Wir sollen einfach die Strukturen erkennen. Dann ist es eher einfach. Es gibt allerdings keine Regel der Form "Klammer vor Punkt vor Strich". Wichtig ist zu erkennen, was bei einer "Verschachtelung" "innen" oder was "außen" ist. Beispiel:
und
Im ersten Fall ist der Bruch innerhalb der Wurzel, also müssen wir erst die Gegenrechnung für die Wurzel und dann für den Bruch benutzen:
Im zweiten Fall ist die Wurzel innerhalb des Bruches, also müssen wir erst die Gegenrechnung für den Bruch und dann für die Wurzel benutzen:
Beim Umformen ist unsere erste Aufgabe den Term (oder die Terme) mit der gesuchten Variable zu isolieren (allein auf einer Seite lassen).
In den folgenden Gleichungen ist immer m die gefragte Variable. In der ersten Spalte sieht man eine Gleichung. Für jede Gleichung haben wir in der zweiten Spalte den Term (bzw. die Terme) mit der gesuchten Variable in einem Rahmen und die gesuchte Variable mit Rot hervorgehoben. In der letzten Spalte sieht man dann diesen Term (bzw. diese Terme) allein auf einer Seite, während alle andere Terme sich auf der anderen Seite befinden.
|
|
| ||||||||
|
|
| ||||||||
|
|
| ||||||||
|
|
| ||||||||
|
|
|
Man sieht in diesen Beispielen, dass der Term mit der gesuchten Variable von den anderen Summanden isoliert wird. Wenn man diesen Schritt schon gemacht hat, sind die weiteren Schritten viel einfacher. Im Folgenden werden wir immer mit der Gleichung der jeweiligen letzten Spalte anfangen.
- Im ersten Fall haben wir die gesuchte Variable im Nenner. Man multipliziert jede Seite als Ganzes mit der gesuchten Variable.
Als Ganzes bedeutet also hier die linke Summe in Klammer zu setzen. Man dividiert dann durch die Klammer und dann haben wir schon das Ergebnis!
oder in einem Bruch:
- Im zweiten Fall
muss man zuerst durch a dividieren und dann Wurzel ziehen. Das Ergebnis ist dann:
oder in einem Bruch geschrieben:
- Im dritten Fall steht die gesuchte Variable in einer Summe im Nenner.
Es gibt verschiedenen Möglichkeiten das Minus weg zu kriegen (z.B. mit -1 multiplizieren). Wir ziehen aber hier vor, das Minus in den Nenner zu bringen, was dazu führt, dass sich die Vorzeichen ändern (also anstatt haben wir ). Wir arbeiten dann wie im ersten Fall aber mit dem Nenner als Ganzes:
und das Ergebnis ist:
- Im viertel Fall befindet sich die gesuchte Variable in mehreren Termen:
Man muss also die gesuchte Variable zuerst herausheben:
und dann durch die dadurch entstandenen Klammer dividieren. Das Endergebnis (wenn man auch den Doppelbruch vereinfacht) ist:
- Im fünften Fall befindet sich die gesuchte Variable innerhalb einer Wurzel im Nenner.
Man soll zuerst den Nenner "oben" bringen, also mit dem Nenner multiplizieren
Als zweites soll die Wurzel allein auf einer Seite bleiben:
Dann soll man die Wurzel "auflösen", in dem man beide Seiten quadriert:
Jetzt steht die gefragte Variable m (quadriert) in einer Summe rechts. Man soll sie erst "isolieren":
und dann einfach Wurzel ziehen:
Funktionen
[Bearbeiten]Funktion allgemein
[Bearbeiten]Wenn man z.B. die Temperaturen um gewissen Uhrzeiten an einem Tag misst, dann hat man schon eine Art von Funktion. Man sagt, dass die Temperatur die abhängige Variable ist und die Uhrzeit die unabhängige. Für jeden Wert der unabhängigen Variable gibt es einen Wert der abhängigen Variable aber für jeden Wert der abhängigen Variable kann es keine, eine oder mehrere Werte der unabhängigen Variable geben.

In unserem Beispiel: für jede Uhrzeit gibt es genau eine Temperatur (es kann nicht mehrere geben), eine Temperatur aber kann nie, einmal oder mehrmals vorkommen. Man kann die ganze Information in einer Tabelle schreiben und mit Hilfe der Tabelle, kann man auch ein Diagramm erstellen:
Wie man im Diagramm ablesen kann, es gibt nur eine Temperatur für jede Uhrzeit (z.B. um 10 Uhr ist die Temperatur 14°C und nicht gleichzeitig 18°C) aber für jede Temperatur kann es keine (z.B. 5°C gibt es nicht), eine (z.B. 10° C gibt es nur um 6 Uhr) oder mehrere Zeiten (z.B. 15°C kommt 2 mal vor, man kann sogar raten, dass es die gleiche Temperatur irgendwann zwischen 10 Uhr und 12 Uhr gab!).
Lineare Funktion
[Bearbeiten]Was ist eine lineare Funktion
[Bearbeiten]Wenn das Diagramm einer Funktion eine Gerade ist, dann geht es um eine sogenannte lineare Funktion. Ein lineare Funktion hat die allgemeine Form:
y=s x +A
wo y die abhängige Variable ist, x die unabhängige Variable und s und A irgendwelche Konstanten (Zahlen, die sich nicht ändern, wie die Variablen). So sind die folgende Funktionen linear:
y=3x – 2 y=-0,5x+130 y= ¾ x – 2,3 y=-√3 x -5
In der ersten Funktion y=3x – 2 ist s=3 und A=-2.
In der zweiten Funktion y=-0,5x+130 ist s=-0,5 und A=130.
In der dritten Funktion y= ¾ x – 2,3 ist s= ¾ und A=-2,3.
In der vierten Funktion y=-√3 x -5 ist s=-√3 und A=-5.
Selbstverständlich kann man statt x und y andere Symbole benutzen:
y=3x – 2, a=3b – 2 und V=3h – 2 sind Darstellungen der gleichen Funktion, es werden nur andere Symbole für x und y benutzt. y= ¾ x – 2,3 ist doch eine andere Funktion, weil s und A (die Konstanten) anders sind. Wenn allein s oder allein A oder beide s und A in zwei Funktionen anders sind, dann haben wir zwei unterschiedlichen linearen Funktion. Wenn s und A in zwei Funktionen gleich sind, dann haben wir die gleiche Funktion, egal welche Symbole wir für x und y benutzen.
In einer linearen Funktion wird die Konstante, mit der x multipliziert wird (hier mit s bezeichnet), Steigung der Funktion genannt. Die Steigung ist ein sehr wichtiger Begriff in der höheren Mathematik. Die Konstante, die dann addiert wird (hier mit A bezeichnet) nennt man y-Achsenabschnitt. Man muss auch sagen: in verschiedenen Staaten benutzt man unterschiedliche Symbole für s und A, z.B.
Hier ist dann m die Steigung und n der y-Achsenabschnitt (Gebrauch in Deutschland) .
Hier ist dann k die Steigung und d der y-Achsenabschnitt (Gebrauch in Österreich) .
Hier ist dann m die Steigung und q der y-Achsenabschnitt (Gebrauch in der Schweiz) .
Hier ist dann m die Steigung und b der y-Achsenabschnitt (Gebrauch in Spanien) .
Hier ist dann a die Steigung und b der y-Achsenabschnitt (Gebrauch in Frankreich und auf Englisch) .
Tabelle für eine lineare Funktion erstellen
[Bearbeiten]Für jede Funktion kann man eine Tabelle machen. Diese Tabelle kann man dann als Punkte in einem Diagramm darstellen. Als Beispiel benutzen wir die Funktion y=3x – 2:

Diagramm einer linearen Funktion mit Hilfe von zwei Punkten erstellen
[Bearbeiten]Um diese Funktion in einem Diagramm darzustellen braucht man nur zwei Punkte. Einen Punkt schreibt man mit einem Wertepaar P:(x|y), wobei erst immer der x-Wert geschrieben wird und dann der y-Wert (innerhalb von Klammern). Benutzen wird beispielsweise PA:(-1|-5) und PB:(2|4) (erstes Bild). Mit Hilfe dieser Punkte kann man eine Gerade ziehen (zweites Bild). Wie man dann feststellen kann, liegen alle Wertepaare der Tabelle auf dieser Gerade! (Drittes Bild)
Das ist genau die Sache. Alle Wertepaare einer linearen Funktion liegen auf der gleichen Gerade! Die Darstellung einer linearen Funktion auf einem Koordinatensystem ist eine Gerade!
Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln
[Bearbeiten]
Wenn man zwei Punkte einer linearen Funktion hat, kann man nicht nur die entsprechende Gerade im Diagramm zeichnen, sondern auch die Funktion selber finden, wenn man sie nicht kennt. Nehmen wir die folgenden zwei Punkte P und Q, die man auch vom Diagramm ablesen kann:
Mit Hilfe der beide Punkten kann man die Funktion in einem Koordinatensystem darstellen, wie im Bild. Wie viel ist die Steigung dieser Funktion und wie viel der y-Achsenabschnitt?
Die allgemeine Gleichung einer linearen Funktion ist:
wobei hier mit s die Steigung gemeint ist und mit A der y-Achsenabschnitt.
Um die Steigung und den y-Achsenabschnitt der im Diagramm dargestellten Funktion zu berechnen, werden wir hier das sogenannte Gleichsetzungsverfahren benutzen. Setzen wir die Wertepaare für die zwei gegebenen Punkten in der allgemeinen Gleichung der linearen Funktion ein:
Formen wir beide Gleichungen auf A um:
Da die rechten Seiten der Gleichungen gleich sind (beide A), sollen auch die linken gleich sein.
und daher
Die Funktion lautet daher:
Für die direkte Berechnung der Steigung s gibt es allerdings eine Formel. Es gilt:
wobei Δy die Differenz der y-Werte der zwei Punkte und Δx die Differenz der x-Werte ist.
In unserem Beispiel sind die Punkte und , also die y-Werte 4 und -2 und die x-Werte 2 und 5. Die entsprechenden Differenzen sind: Δy=4 − ( − 2)=6 und Δx=2-5=-3. Daher ist die Steigung der abgebildeten linearen Funktion, die durch die Punkte P und Q geht:
Die Steigung und ihre Zusammenhänge ==== ===== Beweis der Formel der Steigung einer linearen Funktion =
[Bearbeiten]|
Zeigen Sie, dass die Steigung s |
Wir benutzen hier 2 Punkte, wie in der entsprechenden Aufgabe mit konkreten Zahlen. Diesmal benutzen wir Symbole statt konkreten Zahlen.
Wir formen beide Gleichungen auf A um:
Da die rechten Seiten der Gleichungen gleich sind (beide A),
sollen auch die linken gleich sein.
Das Symbol bedeutet Differenz. und , daher:
Steigung
Zusammenhang linearer Funktion und direkter Proportionalität
[Bearbeiten]Die direkte Proportionalität ist eine lineare Funktion, deren y-Achsenabschnitt A null ist. Wenn wir für die Steigung der linearen Funktion das Symbol s und für den y-Achsenabschnitt das Symbol A, dann lautet die allgemeine Darstellung:
y= s·x + A
Wenn der y-Achsenabschnitt null ist, dann haben wir eine direkte Proportionalität:
y= s·x
Die Steigung ist in diesem Fall das Verhältnis (Quotient) zwischen abhängiger und unabhängiger Variable:
Es gibt allerdings noch einen Zusammenhang zwischen direkter Proportionalität und linearer Gleichung. Die Steigung ist das Verhältnis zwischen Änderung der unabhängigen und Änderung der abhängigen Variable:
Das bedeutet, dass eine direkte Proportionalität zwischen den beiden Änderungen besteht:
Zusammenhang linearer Funktion und Ähnlichkeit ebener Figuren
[Bearbeiten]

und
also, die Quotienten der entsprechenden Seiten sind gleich!
Seite DE ist allerdings 1,5 mal die Seite AB, also um 50% größer als AB. Das gilt allerdings genauso für Seiten EF und BC, also EF ist 50% größer als BC. Man stellt daher fest, dass bei der Ähnlichkeit von Figuren eine direkte Proportionalität (eine lineare Funktion mit y-Achsenabschnitt gleich null) für die Längen der Seiten vorliegt: wird eine Seite größer, dann wird die andere auch und zwar um den gleichen Prozentsatz!
Einheiten der Steigung
[Bearbeiten]

Die Steigung einer Gerade ist allgemein die Differenz zwei y-Werte durch die Differenz der entsprechenden x-Werte, also ein Differenzenquotient (Bild links). Da bei einem s-t Diagramm auf der y-Achse die Strecke dargestellt wird und bei der x die Zeit (Bild rechts), ergibt sich der Quotient:
Steigung:
Der letzte Quotient ist nichts anders als die mittlere Geschwindigkeit:
Daher:
Die Steigung in einem s-t Diagramm zeigt uns die Geschwindigkeit
Im konkreten Beispiel rechts: s1 ist zwei Einheiten, s2 5 Einheiten. Wenn die Einheiten der y-Achse Meter (m) sind, ist Δs=3 m. Entsprechend, wenn die Einheit auf der x-Achse Sekunde (s) ist, dann ist Δt=6 s. Die Steigung und daher auch die Geschwindigkeit ist in diesem Fall


Entsprechend können wir die physikalische Größe und die Einheiten der Steigung in einem v-t Diagramm finden. Da bei einem v-t Diagramm auf der y-Achse die Geschwindigkeit dargestellt wird und bei der x die Zeit (Bild rechts), ergibt sich der Quotient:
Steigung </math>
Die Steigung zeigt uns in diesem Fall eine Änderung der Geschwindigkeit, also eine Beschleunigung:
Daher:
Die Steigung in einem v-t Diagramm zeigt uns die Beschleunigung
Im konkreten Beispiel rechts: ist 2 Einheiten, 5 Einheiten, daher, wenn die Einheiten m/s (Meter pro Sekunde) sind, ist , und für Sekunde als Einheit auf der x-Achse ist . Die Steigung und daher auch die Beschleunigung ist in diesem Fall:
Von diesen Beispielen wird daher klar:
Die Steigung ist eine Änderungsrate, sie zeigt wie schnell sich die Größe der y-Achse in Bezug auf die Größer der x-Achse ändert. Die Einheiten der Steigung sind daher die Einheiten der y-Achse durch die Einheiten der x-Achse.
Noch zwei Beispiele: Wenn auf der y-Achse Kraft (in Newton) dargestellt wird und auf der x Fläche (in m2), dann ist die physikalische Größe der Steigung Druck (also Kraft durch Fläche) und die Einheit Pa (Pascal, also Newton durch m2). Wenn auf der y-Achse Masse (in kg) steht und auf der x Volumen (in ), dann ist die physikalische Größe der Steigung Dichte (also Masse durch Volumen) und ihre Einheiten kg/.
Textaufgaben zu den linearen Funktionen
[Bearbeiten]Die andere Konstante wird dann der y-Achsenabschnitt sein. Die Einheit des y-Achsenabschnitts ist auch die Einheit der abhängigen Variable und auch die erwähnte Einheit A bei der Steigung. Damit haben wir alle Elemente in einem mathematischen Zusammenhang „übersetzt“.
- Beim Taxifahren ist die Grundgebühr 4€ und jede Minute kostet dann 0,5€. Stelle diesen Zusammenhang als lineare Funktion dar.
Lösung:
Hier sind zwei Zahlen angegeben: 4€ und 0,5€. Über 0,5€ ist aber auch gesagt, dass man "jede Minute" 0,5€ zahlt. Anders ausgedrückt sind es 0,5€ pro Minute. Einheit A (€) durch Einheit B (min). Das heißt, es geht um eine Änderungsrate. 0,5 soll also unsere Steigung sein. Dann ist die Grundgebühr der y-Achsenabschnitt. Die abhängige Variable wird also in € ausgedrückt (wie die Grundgebühr und die Einheit A oben in der Steigung), die unabhängige in Minuten (wie die Einheit B, die Einheit, die in der Steigung unten steht). Für beide Variablen kann man frei irgendwelche Symbole auswählen, gewöhnlich sollen sie auch sinnvoll sein, z.B. hier K für die Kosten und t für die Zeit (Englisch: time):
K(t)= 0,5 t + 4 (t in Minuten, K in €)
Man soll auch eine Entscheidung über das Vorzeichen der Steigung treffen. Das ist eher einfach. Wenn es klar ist, dass die abhängige Variable (z.B. y, hier die Kosten K) auch größer wird, wenn die unabhängige (z.B. x, hier die Zeit t) größer wird, dann ist die Steigung positiv. Bei den Kosten ist es klar, dass sie immer mehr werden, wenn die Fahrt länger dauert. Also ist die Steigung positiv.
Wenn aber es klar ist, dass die unabhängige Variable kleiner wird, wenn die unabhängige größer wird, dann ist die Steigung negativ. Schauen wir ein entsprechendes Beispiel.
- Eine Kerze mit einer Länge von 1,8 dm wird angezündet. Dabei brennt sie stündlich um ca. 0,9 cm ab. Stelle diesen Zusammenhang als lineare Funktion dar.
Hier ist 0,9 cm eine Änderungsrate, also 0,9 cm pro Stunde. 0,9 ist also die Steigung. Die Kerze wird aber immer kürzer, also wird die Steigung negativ sein. 1,8 dm wird unserer y-Achsenabschnitt sein. Wir wählen L für die Länge und t für die Zeit aus:
L(t)= - 0,9 t + 18 (t in Stunden, L in cm)
Vorsicht!
Man soll immer die Einheiten schreiben und die richtigen Einheiten benutzen.
Wenn man beispielsweise für den Abstand die Einheit Meter benutzt, muss man alle angegebene Abstände in Meter umwandeln, wenn sie nicht schon in Meter angegeben sind. Der vorsichtige Leser hat vielleicht gemerkt, dass der y-Achsenabschnitt in der Funktion 18 und nicht 1,8 ist. Wir haben erst die 1,8dm in 18cm umgewandelt! Das ist notwendig, weil die Steigung in cm (und nicht dm) pro Stunde gegeben ist. Ähnlich, wenn der Wert für die Zeit in Minuten gegeben ist, muss man sie erst in Stunden umwandeln (die Steigung ist ja pro Stunden). Darauf muss man also immer aufpassen!
Schauen wir ein etwas komplexeres Beispiel.
- Der Druck in der Atmosphäre eines Planeten ist durch eine lineare Funktion angegeben. Auf 50km Höhe ist er 3 Atm, auf 200 km 1,8 Atm. Wie viel ist der Druck
- auf der Oberfläche des Planeten?
- auf 300 km Höhe?
- 50 km unterhalb der Oberfläche?
In diesem Fall muss man erst die lineare Funktion mit Hilfe der beiden Punkte finden. Der aufmerksame Leser hat vielleicht schon gesehen, dass die gegebenen Punkte hier sind. Wie im vorherigen Teil gezeigt, man kann die Funktion in zwei verschiedenen Weisen finden:
Man kann das lineare Gleichungssystem lösen:
| P(x|y) | x | y | y=mx+n |
|---|---|---|---|
| P(50|3) | 50 | 3 | 3=m·50+n |
| Q(200|1,8) | 200 | 1,8 | −1,8=m·200+n |
oder man kann direkt die Formel für die Steigung benutzen:
und dann den y-Achsenabschnitt finden.
Selbstverständlich bekommt man in beiden Fällen die gleiche Antwort:
m=-0,008 und n=3,4 also
Mit Hilfe der Funktion kann man jetzt die Fragen beantworten.
- Auf der Oberfläche ist die Höhe (also der x-Wert) Null. Das ist der y-Achsenabschnitt, also 3,4 Atm
- In der zweiten Frage setzt man die 300 km für den x-Wert ein: , also 1 Atm.
- In der dritten Frage muss man denken, dass unterhalb der Oberfläche die Höhe negativ sein wird: also 3,8 Atm.
Darstellungen der linearen Funktion
[Bearbeiten]Die explizite Form
[Bearbeiten]- Die Darstellung y=a⋅x+b der linearen Funktion nennt man explizite Form.
- In dieser Form steht die abhängige Variable y auf der rechten Seite und auf der linken die unabhängige Variable x - mit einer Konstante a (bzw. d, m usw.) vor ihr - plus eine zweite Konstante b (bzw. d, n usw.). Es gibt aber auch andere Darstellungen der linearen Funktion.
Die implizite Form
[Bearbeiten]- Die implizite Form ist:
- a⋅x+b⋅y+c=0 (oder a⋅x+b⋅y=c)
Die Parameterform (Vektorform)
[Bearbeiten]Die Parameterform wird durch zwei Gleichungen angegeben:
Die Variable t nennt man Parameter
Das gleich kann man in der sogenannten Vektorform darstellen:
und sind Vektoren, nämlich :
Diese Darstellung ist gleichbedeutend mit den folgenden zwei Gleichungen:
Es ist oft so in der Vektorrechnung, dass die Achsen des Koordinatensystems durchnummeriert werden. Hier steht an der Stelle von und an der Stelle von .
Graphische Darstellung
[Bearbeiten]
Wie schon beschrieben kann man Geometrie und Algebra kombinieren. Wir haben dort gesehen, dass die algebraische Form eines Kreises x2+y2=r2 ist.
Die geometrische Form einer linearen Gleichung in einem kartesischen Koordinatensystem ist eine Gerade:
In diesem Bild haben die rote und die grüne Gerade den gleichen y-Achsenabschnitt, die rote und die blaue die gleiche Steigung (sie sind parallel). Die blaue und die grüne haben einen gemeinsamen Punkt bei (-4/3|-5/3)
Umwandeln von einer Form zu einer anderen
[Bearbeiten]Im folgenden werden die unterschiedlichen Symbole für die explizite Form benutzt, die in den verschiedenen deutschsprachigen Staaten benutzt werden. Nochmal:
y=k⋅x+d ist gleich wie y=m⋅x+n ist gleich wie y=m⋅x+q
Wichtig ist nur zu wissen:
Die Konstante, die in der explizite Form mit x multipliziert wird, ist die Steigung. (in der Schweiz und in Deutschland m, in Österreich k - in der Regel!)
Die Konstante, die zu diesem Produkt addiert wird, ist der y-Achsenabschnitt. (in der Schweiz q, in Deutschland n, in Österreich d - in der Regel!)
Explizite zur impliziten Form
[Bearbeiten]y=k⋅x+d ⇔ -k⋅x+y-d=0
Das ist schon die implizite Form a⋅x+b⋅y+c=0 mit
-k statt a (Konstante vor x in der impliziten Form),
1 statt b (Konstante vor y in der impliziten Form) und
-d statt c (Konstante ohne Variable in der impliziten Form).
Explizite zur Parameterform
[Bearbeiten]y=m⋅x+n
Wenn wir x=t stellen, dann haben wir schon die Parameterform:
| x=t y=m⋅t+n |
Vektorform: |
Vergleichen wir das mit dem allgemeineren Parameterform (x=a1⋅t+b1 und y=a2⋅t+b2), dann stellen wir fest, dass hier a1=1, b1=0, a2=m und b2=n ist.
Implizite zur expliziten Form
[Bearbeiten]a⋅x+b⋅y+c=0
Mit unseren Kenntnissen können wir diese Gleichung auf y umformen:
a⋅x+b⋅y+c=0 ⇔ b⋅y=-c-a⋅x und daher:
Das ist die explizite Form mit -a/b als Steigung (m, k usw.) und -c/b als y-Achsenabschnitt (n,p,d usw.).
Implizite zur Parameterform
[Bearbeiten]Man nimmt das Ergebnis aus dem letzten Abschnitt und wandelt diese explizite in die Parameterform:
| Vektorform: |
Parameter- zur expliziten Form
[Bearbeiten]| x=a1⋅t+b1 y=a2⋅t+b2 |
Vektorform: |
Man formt die erste Gleichung auf t um und setzt dieses t in die zweite Gleichung ein:
Die Steigung in der Parameterform ist daher und
der y-Achsenabschnitt ist
Parameter- zur impliziten Form
[Bearbeiten]Man benutzt die Gleichung aus dem letzten Abschnitt und formt sie um:
Das ist schon die implizite Form a⋅x+b⋅y+c=0 mit
statt a (Konstante vor x in der impliziten Form),
statt b (Konstante vor y in der impliziten Form) und
statt c (Konstante ohne Variable in der impliziten Form).
Die lineare Funktion graphisch darstellen
[Bearbeiten]Durch die Definition der Gerade versteht man, dass zwei Punkte ausreichen, um eine Gerade eindeutig zu definieren. Ein Punkt ist durch zwei Werte bestimmt, die x-Koordinate und die entsprechende y-Koordinate. Um zwei Punkte einer linearen Funktion zu finden, reicht es daher aus, willkürlich zwei Werte für x in der Funktion einzugeben und die entsprechende Werte für y finden. Diese zwei Punkte zeichnet man dann im Koordinaten System. Die Gerade, die durch diese zwei Punkte läuft, entspricht der gegebenen linearen Funktion.
Lösung(en) einer Funktion
[Bearbeiten]Schnittpunkte von Funktionen
[Bearbeiten]
| Diagramm |
| Text |

Hier sind ein paar Beispiele von Funktionen:
f(x)=3x−5 K(s)=3s+1,5 V(r,h)=πr²(r+h)
h(t)=14− 3t ρ(m,V)=
Oft haben wir erwähnt, dass wenn nichts zwischen zwei mathematischen Ausdrücken steht, eine Multiplikation gemeint ist. In diesen Fällen ist allerdings nicht so. Mit dem Symbol f(x) ist eine Funktion f gemeint, wo die abhängige Variable durch f (in diesem Fall auch y) und die unabhängige durch x symbolisiert wird. f(x) bedeutet so viel wie „f in Abhängigkeit von x“. Entsprechend könnte K(s) die Kosten einer Taxifahrt in Abhängigkeit vom Abstand s bedeuten, V(r,h) das Volumen V eines zusammengesetzten geometrischen Körpers in Abhängigkeit von dem Radius r und der Höhe h, h(t) die Höhe einer Kerze in Abhängigkeit von der Zeit oder ρ(m,V) die Dichte in Abhängigkeit von der Masse und das Volumen. Selbstverständlich können alle diese Symbole auch etwas anderes als Kosten, Volumen, Radius, Zeit usw. bedeuten und jedes Symbol kann mal die unabhängige und mal die abhängige Variable sein (wie hier mit dem Volumen). In der Symbolik a(u) ist das (oder die) Symbol im Klammer (hier u) die unabhängige Variable, die auf der x-Achse dargestellt wird und das Symbol außerhalb (vor) der Klammer (hier a) die abhängige.

In einer Funktion kann es für jeden Wert der unabhängigen Variable genau einen Wert der abhängigen geben, für jeden Wert der abhängigen allerdings keine, eine oder mehrere Werte der unabhängigen. Die Menge der Werte der unabhängigen Variable wird Definitionsmenge genannt, die Menge der Werte der abhängigen Zielmenge. Obwohl für die Zielmenge oft das Wort Wertemenge benutzt wird, sind in der Schulmathematik i.d.R. nur die Werte der Zielmenge, die tatsächlich einem Wert der Definitionsmenge entsprechen, mit Wertemenge gemeint. Im Bild ist A die Definitionsmenge, B die Zielmenge und {b,c,d} die Wertemenge. B kann in diesem Fall nicht die Definitionsmenge sein, da {b} zwei Werten von A entspricht. Mit dem Wort „Stelle“ ist ein Wert aus der Definitionsmenge gemeint („x-Wert“), mit dem Ausdruck „Wert der Funktion“ ein Wert aus der Zielmenge („y-Wert“). Wenn der Wert einer Funktion (y-Wert) an einer gewissen Stelle gefragt wird, dann muss man die unabhängige Variable in der Funktion durch ihren angegebenen Wert („Stelle“, x-Wert) ersetzen. Wenn z.B. die Funktion g(a)=a²+4a−11 ist, dann ist der Wert der Funktion an der Stelle 2 gleich g(2)=2²+4·2−11 also 1. Wie zu sehen ist, haben wir bei g(2) überall, wo in der Funktion g(a)=a²+4a−11 das a steht, dieses durch 2 ersetzt und damit den Wert der Funktion an dieser Stelle berechnet. Es gilt daher in dieser Funktion: g(2)=1.
Mit dem Begriff „Lösungen“ einer Funktion sind die Stellen (x-Werte) der Funktion gemeint, wo die Funktion gleich Null ist, also wo die x-Achse von der Funktion geschnitten oder berührt wird und wo der y-Wert Null ist. Im Diagramm sind die Punkte B, C, D und E Lösungen der Funktion, die durch die Kurve dargestellt wird. Der Punkt F ist die Lösung der Funktion, die mit einer Gerade dargestellt wird. Wenn nicht ein Diagramm sondern der "algebraische" Ausdruck der Funktion gegeben ist, dann sollen wir die Funktion gleich Null setzen, um die Lösungen zu finden. Beispielsweise müssen wir die Funktion k(x)=x4−5x3+4x gleich Null setzen, u ihre Lösungen (Nullstellen) zu finden:
0=x4−5x3+4x
Diese Gleichung stimmt für x gleich ca. −0,83, 0, 1 und ca. 4,83. Diese Stellen (: Werte von x) sind die Lösungen der Funktion (Nullstellen: Stellen, also Werten von x, wo die Funktion, also die Werte von y, Null ist).
Der y-Achsenabschnitt für eine Gerade haben wir schon gelernt, für die Kurve im Diagramm ist er der Punkt A. An diesem Punkt ist der x-Wert Null (wie allerdings auf der ganzen y-Achse). Wenn wir den Wert der Funktion g(a)=a²+4a−11 a an der Stelle 0 (x-Wert, also die unabhängige Variable ist Null, also hier a=0), dann bekommen wir den Wert g(0)=0²+4∙0−11=−11. Alle Teilterme, die x haben, werden bei der Berechnung des y-Achsenabschnitts einfach ausgelassen (da sie mit Null multipliziert werden). Der y-Achsenabschnitt der Kurve im Diagramm ist 1 (Punkt A), der Gerade 13 (nicht sichtbar).
Lösung eines Gleichungssystems sind die Punkte, wo die Funktionen einander schneiden. Im Bild sind es die Punkte G, H, I. Da schneiden die Kurve und die gerade einander. Um diese Punkte zu finden, werden die beide Funktionen gleich zueinander gestellt. Wenn z.B. die Kurve k(x)=x⁵+4x³-3x²+1 wäre und die Gerade f(x)=−2x+13, dann schreibt man: k(x)=f(x) also x⁵+4x³-3x²+1=−2x+13 und löst diese Gleichung. Das funktioniert, weil die beiden Funktionen an den Schnittpunkten die gleichen y-Werte haben (also ist an diesen Punkten tatsächlich k(x)=f(x)) und auch die gleichen x-Werte.
Der Punkt K gehört zur Kurve aber nicht zur Gerade, Punkt J gehört zu keiner der beiden Funktionen. Um herauszufinden, ob ein Punkt zu einer Funktion gehört, setzen wir in der Funktion den Wert von x ein und vergleichen wir das Ergebnis (y-Wert) mit dem y-Wert des Punktes. Wenn diese dann übereinstimmen, dann gehört der Punkt zur Funktion, sonst nicht.
Die quadratische Funktion
[Bearbeiten]Die quadratische Gleichung
[Bearbeiten]| Eine Funktion der Form wird quadratische Funktion genannt. Ihre Lösungen |
| Der Ausdruck unter der Wurzel wird Diskriminante genannt. |
| Wenn die Diskriminante positiv ist, hat die Gleichung zwei Lösungen, wenn null dann eine Lösung und wenn negativ |
Eine Polynomfunktion ist eine Funktion von einer Summe von Potenzfunktionen, deren Hochzahlen natürliche Zahlen sind:
n ist die größte Hochzahl und bestimmt den sogenannten Grad der Funktion (für an≠0), an, an-1, … , a0 sind die sogenannten Koeffizienten. Wenn n=2 ist, dann ist von einer quadratische Funktion die Rede:Q(x)= ax²+bx+c
Wir beschäftigen uns in diesem Kapitel mit den Lösungen einer quadratischen Funktion, also mit den Stellen der Funktion, wo ihre Wert Null ist. Wir setzen daher die Funktion gleich Null. Die entsprechende Gleichung wird quadratische Gleichung genannt:
ax²+bx+c=0
Fangen wir mit einem einfachen Beispiel an:
x²=9
Die Gegenrechnung von Quadrat ist die Wurzel:
also x=3
Ist das jetzt die einzige Lösung dieser Gleichung? Nein. Auch der Wert −3 ist eine Lösung der Gleichung:
(−3)²=9
Daher ist es notwendig, bei solchen Fällen beide Lösungen zu schreiben:
also sowohl +3 als auch −3
Allerdings haben wir die quadratische Gleichung in der folgenden Form geschrieben:
ax²+bx+c=0
In der Gleichung x²=9 haben wir rechts doch nicht null sondern 9. Wie so haben wir behauptet, dass es um eine quadratische Gleichung geht? Das wird klar, wenn 9 auf die andere Seite gebracht wird:
x²−9=0
Das ist eine quadratische Gleichung mit a=1, b=0 und c=−9. Das ist allerdings auch die plus-minus binomische Formel, die als Produkt geschrieben werden kann:
x²−9=0 → (x+3)(x−3)=0 also x=−3 oder x=3
Wir haben also gesehen, dass die quadratische Funktion f(x)=x²−9, also die entsprechende Gleichung x²−9=0, zwei Lösungen hat. Ist das immer der Fall, dass eine quadratische Funktion und die entsprechende Gleichung zwei Lösungen hat? Nehmen wir folgendes Beispiel:
x²+10x+25=0
Das ist eine quadratische Gleichung mit a=1, b=10 und c=25. Der Term links ist wieder eine binomische Formel, die plus Formel:
x²+10x+25=0 → (x+5)²=0 → (x+5)(x+5)=0 also x=−5
Wie zu sehen ist, gibt es hier nur eine (sozusagen doppelte) Lösung, nämlich x=−5. Nehmen wir noch ein Beispiel:
x²=−3
Die Gegenrechnung ist die Wurzel:
Die Wurzel von negativen Zahlen ist (in der Menge der reellen Zahlen) nicht definierbar. Eine Erklärung ist, dass das Quadrat von allen Zahlen (positiven und negativen) nie negativ sein kann. Beispielsweise ist 3²=9 positiv aber (−3)²=9 auch. Daher hat die Gleichung x²=−3 keine Lösung. Bringen wir in der Gleichung die 3 auf die andere Seite:
x²+3=0
Vergleichen wir das mit der allgemeinen quadratischen Gleichung:
ax²+bx+c=0
sehen wir, dass in x²+3=0 das a gleich 1, das b gleich 0 und das c gleich 3 sein soll. So haben wir eine quadratische Gleichung mit a=1, b=0 und c=3. Diese Gleichung hat allerdings keine Lösung (in der Menge der reellen Zahlen). Wir haben also in den vorherigen Beispielen gesehen:
Eine quadratische Gleichung (und die entsprechende Funktion) kann keine, eine oder zwei Lösungen haben.
Es gibt eine Formel für die Lösungen der allgemeiner quadratische Funktion ax²+bx+c=0:
Der Ausdruck unter der Wurzel wird Diskriminante D genannt.
Wenn die Diskriminante positiv ist, hat die Gleichung zwei Lösungen , wenn null dann eine Lösung und wenn negativ keine (da es keine Wurzel von negativen Zahlen gibt). In unseren Beispielen:
- x²=9 also x²−9=0 Hier ist a=1, b=0 und c=−9.
Diskriminante: D=b²−4ac=0²−4·1·(−9)=36>0 (positiv). Es gibt daher 2 Lösungen.
- (x+5)²=0 also x²+10x+25=0 Hier ist a=1, b=10 und c=25.
Diskriminante: D=b²−4ac=10²−4·1·25=100−100=0 (null). Es gibt daher 1 Lösung.
- x²=−3 also x²+3=0 Hier ist a=1, b=0 und c=3.
Diskriminante: D=b²−4ac=0²−4·1·3=−12<0 (negativ). Es gibt daher keine Lösung.
- (x+5)²=9 also x²+10x+16=0 Hier ist a=1, b=10 und c=16.
Diskriminante: D=b²−4ac=10²−4·1·16=100−64=36>0 (positiv). Es gibt daher 2 Lösungen.
Quadratische Gleichung Textaufgaben
[Bearbeiten]Lineare Gleichungssysteme mit 2 Variablen
[Bearbeiten]Einsetzungsverfahren
[Bearbeiten]Wie löst man so eine Aufgabe? Man benutzt ein sogenanntes lineares Gleichungssystem. Wir werden uns hier mit der einfachste Form eines Gleichungssystems beschäftigen, einem Gleichungssystem mit zwei unbekannten und zwei Gleichungen. Es gibt verschiedene Wege so ein System zu lösen, wir werden hier zunächst einmal einen Weg zeigen.
Hier gibt es zwei unbekannte, die Anzahl der Tische für 3 Personen und die Anzahl der Tische für 5 Personen. Wenn man in Mathematik etwas nicht kennt, benutzt man ein Symbol dafür, in der Regel (kann aber a, b, z, A1, oder irgendwas sein). Lass uns dann mit die Anzahl der Tische für 3 Personen bezeichnen. Wir wissen nicht, ob die Anzahl der Tische für 5 Personen gleich so groß wie die Anzahl der Tische für 3 Personen ist. Daher müssen wir für die Anzahl der Tische für 5 Personen ein anderes Symbol benutzen, z.B. . Also:
: die Anzahl der Tische für 3 Personen
: die Anzahl der Tische für 5 Personen
Wie schon gesagt, wir wissen nicht, wie viele Tische es für 3 oder für 5 Personen gibt. Wir wissen aber schon, dass es insgesamt 8 Tische gibt. Also die x Tische und die y Tische zusammen sind 8 Tische:
Die Tische sind für 3 Personen. Wir wissen zwar nicht, wie viel ist, aber wir können sagen, dass
| 1 Tisch → | (3 · 1 =) | 3 | Personen |
| 2 Tische → | (3 · 2 =) | 6 | Personen |
| 5 Tische → | (3 · 5 =) | 15 | Personen |
| 8 Tische → | (3 · 8 =) | 24 | Personen also |
| x Tische → | (3 · x =) | Personen |
da wir x Tische haben, anstatt eine bestimmte Zahl, wie 1, 2, 5 oder 8 Tische.
In der gleichen Weise kann man sagen, dass die Tische (für 5 Personen) Gäste bedienen können.
Wir haben also Personen an den Tischen und Personen an den Tischen.
Wir wissen jetzt nicht, wie viel 3x oder 5y ist (das sind Personen), wir wissen aber, dass insgesamt 36 Personen bedient werden können, also:
Wir schreiben jetzt beide Gleichungen zusammen:
Mit einer Gleichung können wir weder x noch y finden, wir können aber hier die erste Gleichung (am einfachsten) umformen:
Da wir es wissen, dass x=8−y ist, können wir dann in der zweiten Gleichung statt x, 8−y schreiben:
(x wird also durch 8-y ersetzt)
Jetzt haben wir eine Gleichung mit einem Unbekannten. So was können wir schon lösen, wie wir beim Kapitel Umformen gelernt haben:
| |Klammer auflösen | |
| |-24 (und y zusammenrechnen) | |
| | :2 | |
y sind die Tische mit 5 Personen. Es gibt also 6 Tische für 5 Personen. Wie viele sind die restlichen? Wir benutzen unsere Gleichung:
Es gibt also x=2 Tische für 3 Personen und y=6 Tische für 5 Personen. Somit haben wir die Aufgabe gelöst!
Lineare Gleichungssysteme Begriffe
[Bearbeiten]Lass uns jetzt ein paar Begriffe erklären.
Eine Gleichung ist ein mathematischer Ausdruck, der das Symbol „=“ („ist“, „gleich“ oder „ist gleich“ ausgedrückt) zumindest einmal beinhaltet und bei dem auf beide Seiten des Symbols „=“ andere mathematische Ausdrücke stehen. „6+3=“ ist noch keine Gleichung, „6+3=9“ oder „6+3=x“ oder „6+y=x“ schon.
Wenn alle Variablen in der Gleichung ohne Hochzahl oder sonst was vorkommen, dann spricht man von einer linearen Gleichung(1). oder oder sind lineare Gleichungen. , oder hingegen nicht (letztere weil im Nenner ist).
Eine Gleichung kann keine, eine oder mehrere Variablen beinhalten. hat keine Variable (und ist allerdings eine wahre Aussage: 6+3 ist tatsächlich 9). , , haben eine Variable. , und haben zwei Variablen.
Wenn man zwei oder mehrere Gleichungen irgendwie verbindet, dann hat man ein Gleichungssystem. In diesem Kapitel haben wir 2 Gleichungen je mit 2 unbekannten gehabt:
Da beide Gleichungen hier linear sind, spricht man von einem linearen Gleichungssystem. So ein System kann man in verschiedenen Wege lösen. Der Weg, den wir hier benutzt haben, nennt man Einsetzungsverfahren. Es gibt dann noch das Gleichsetzungsverfahren und das Additionsverfahren (wir werden sie gleich lernen). Das Einsetzungsverfahren ist sehr wichtig (auch in anderen Wissenschaften, wie in der Physik), da man es leicht auch bei nicht lineare Gleichungssysteme anwenden kann. Dieses Thema ist von einem höheren Niveau und daher nicht in diesem Buch behandelt.
Die Zahlen (manchmal aber auch Symbole), die vor den Variablen stehen und mit diesen multipliziert werden, nennt man Koeffizienten. In der zweiten Gleichung () ist der Koeffizient von 3 und von 5. In der ersten Gleichung () steht keine Zahl vor den Variablen. Trotzdem sagt man dann, dass der Koeffizient 1 ist (es gilt ja, dass und ist). Bei ist der x-Koeffizient , der y-Koeffizient und der z-Koeffizient . Die Symbole c und d sind in dieser Gleichung nicht Variablen (das ist aber nicht immer klar, man soll in solchen Fällen immer die Vorgaben lesen). Wenn ein Symbol benutzt wird, der eine feste Zahl (und daher keine Variable) darstellt, dann nennt man diese Symbol eine Konstante. Die Konstante c ist hier gleichzeitig der Koeffizient der Variablen v. Die Konstante d hingegen ist keiner Koeffizient.
Ein Gleichungssystem kann keine, zwei oder unendlich viele Lösungen haben. Das ist allerdings Thema eines anderen Kapitels.
Gleichsetzungsverfahren
[Bearbeiten]
Formen wir beide Gleichungen auf um:
- Die erste Gleichung geht leicht:
daher
- Die zweite Gleichung ist etwas schwerer:
| |-5y | |
| |:3 | |
Das Gleichungssystem sieht jetzt wie in Folgendem aus:
Da beide Ausdrücke rechts der beiden Gleichungen gleich mit sind, sind sie auch zueinander gleich:
Jetzt haben wir eine Gleichung mit einer Unbekannte, was man mit Umformen lösen kann:
| |⋅3 | |
| |(Klammer auflösen) | |
| |−36+3y | |
| |:(−2) | |
und daher
Die Antwort ist:
und
also genau wie vorher, wie es zu erwarten war.
Additionsverfahren
[Bearbeiten]
Nehmen wir hier die Variable (man kann aber genauso die Variable benutzen). Der y-Koeffizient in der ersten Gleichung ist 3 und in der zweiten 2. Wenn wir den ersten Koeffizient mit 2 multiplizieren und den zweiten mit -3 bekommen wir 6 und ihre Gegenzahl -6. Wenn wir beide Seiten der ersten Gleichung mit 2 multiplizieren, dann haben wir auf beiden Seiten das Gleiche gemacht und beide Seiten werden weiter gleich bleiben (siehe Gegenrechnungen). Ebenfalls wenn wir beide Seiten der zweiten Gleichung mit -3 multiplizieren, bleiben beide Seiten dieser Gleichung gleich:
Wenn wir jetzt die Summe der linken Seiten und die Summe der rechten Seiten beider Gleichungen berechnen, werden die Ergebnisse gleich sein:
Zauberei! Jetzt haben wir nur eine Gleichung mit einem Unbekannten, die wir sofort lösen können!
Wenn wir jetzt eine der beiden Anfangsgleichungen nehmen, können wir auch y berechnen. Nehmen wir die erste:
(x ist -2, wie wir gerade berechnet haben)
|+4
|:3
Die Lösung des Gleichungssystems lautet daher:
und
Tatsächlich kann man diese Werte in beiden Gleichungen einsetzen und feststellen, dass das Ergebnis stimmt. Ersetzen wir in beiden Gleichungen x durch -2 und y durch 5, dann bekommen wir eine wahre Aussage:
Es gibt kein anderes Zahlenpaar, der beide Gleichungen richtig löst, also die Lösung ist eindeutig! Ist es aber immer so? Das ist das Thema des nächsten Unterkapitels.
Graphische Lösung eines linearen Gleichungssystems
[Bearbeiten]Im Kapitel über lineare Funktionen wird erklärt, wie man in einem Koordinatensystem eine lineare Funktion mit Hilfe von zwei Punkten zeichnen kann (zwei Punkte sind eine hinreichende und notwendige Voraussetzung, um eine lineare Funktion zu definieren; daher reichen zwei Punkte um die Funktion zu zeichnen). Nehmen wir die erste Funktion vom folgendem Gleichungssystem:
| (Funktion A) | |
| (Funktion B) |
-
Funktion A
-
Funktion B
-
Funktion A und B
Man kann zwei Punkte für die Funktion finden, indem man willkürlich Werte für x angibt und die entsprechenden Werte für y findet. Für ist:
→ → → .
Für ist:
→ → → .
Wir haben also zwei Punkte der Funktion A: und . Diese Punkte können wir dann im Koordinatensystem zeichnen und auch die Gerade, die der Funktion entspricht, wie im Bild „Funktion A“.
Entsprechend kann man Punkte für die Funktion B finden. Für ist:
→ → → → .
Für ist :
→ → → → .
Wir haben also zwei Punkte der Funktion B: und . Diese Punkte können wir dann im Koordinatensystem zeichnen und auch die Gerade, die der Funktion entspricht, wie im Bild „Funktion B“.
Wenn wir jetzt beide Funktionen in einem Koordinatensystem zeichnen, dann bekommen wir das Bild „Funktion A und B“. Da kann man klar sehen, dass die Funktionen einander an einem einzigen Punkt schneiden, den Punkt . Dieser Punkt ist die Lösung des Gleichungssystems der Funktionen A und B. Leider kann man i.d.R. den - und den -Wert nicht genau ablesen, daher ist diese Methode nicht so genau, wie die drei Verfahren der vorherigen Absätzen.
Lösungsmenge eines linearen Gleichungssystems
[Bearbeiten]| Gleichungssystem A | Gleichungssystem B | |
|---|---|---|
Die Lösung des ersten linearen Gleichungssystems war und , des zweitens und . Geht es aber immer, dass ein Gleichungssystem eine Lösung hat? Die Antwort ist nein. Probieren wir das folgendes Gleichungssystem mit dem Einsetzungsverfahren zu lösen:
| Gleichungssystem C |
|---|
Lösung
→
→ → → !
Man sagt, dass die Aussage am Ende falsch ist. ist doch nicht gleich ! Das bedeutet, dass die beiden Gleichungen, die wir im Gleichungssystem haben ( und ), nicht gleichzeitig erfüllt werden können. Man sagt, dass das Gleichungssystem keine Lösung hat.
Es gibt allerdings noch eine Möglichkeit. Das Gleichungssystem kann unendlich viele Lösungen haben, wie im folgenden Beispiel:
| Gleichungssystem D |
|---|
Lösung
→
→ → →
Man sagt, dass die Aussage am Ende immer wahr ist. Egal wie viel ist, die beiden Gleichungen werden immer gelten. Man soll doch etwas vorsichtig sein. Wenn ist, dann ist (erste Gleichung → → → ). Wenn ist, dann ist (erste Gleichung → → → ). Für jedes gibt es ein bestimmtes und umgekehrt.
Allerdings gilt genau das Gleiche in der zweiten Gleichung: Wenn ist, ist ( → → → ). Wenn ist, dann ist ( → → → ). Egal welchen Wert man für benutzt, wird es für beide Gleichungen der gleiche Wert für als Lösung gelten (und umgekehrt). Es gilt nicht, dass alle Wertepaare (alle Punkte auf der Ebene) Lösungen des Gleichungssystems sind, sondern dass alle Lösungen der einen Gleichung auch Lösungen der anderen Gleichung sind.
Das war allerdings nicht der Fall, als wir eine Lösung des Gleichungssystems hatten (und auf gar keinen Fall, als wir keine Lösung hatten). Nehmen wir beispielsweise das Gleichungssystem A:
6
Da haben wir als Lösung und gefunden. Diese Lösung gilt gleichzeitig für beide Gleichungen. Tatsächlich wenn ist, dann gilt für die erste Gleichung ( → → →) aber auch für die zweite Gleichung ( → → →) . Wenn aber , dann gilt für die erste Gleichung ( → → →) . Für die zweite Gleichung hingegen gilt in diesem Fall: ( → → →) . Die beiden Gleichungen haben den gleichen Wert für y(den Wert 6), nur wenn ist. Man sagt, dass Gleichungssystem A und B eine Lösung haben, Gleichungssystem C keine und Gleichungssystem D unendlich viele Lösungen haben.
Ein lineares Gleichungssystem kann keine, eine oder unendlich viele Lösungen haben.
Viel besser kann man das Ganze verstehen, wenn man die graphischen Lösungen betrachtet.
-
Gleichungssystem A
-
Gleichungssystem B
-
Gleichungssystem C
-
Gleichungssystem D
Im Gleichungssystem A gibt es nur ein Wertepaar, das für beide Funktionen stimmt: . Wenn ist, dann ist für beide Funktionen. Für jeden anderen Wert von x stimmt der Wert von y nicht mehr überein. Beispielsweise für ist für die Funktion und für die Funktion . Es gibt nur ein Wertepaar, das für beide Funktionen eine Lösung ist, und dieses Wertepaar (also der Punkt ) ist die Lösung des Gleichungssystems.
Entsprechend hat auch das Gleichungssystem B nur eine Lösung, den Punkt (Wertepaar) , wie man eindeutig im entsprechenden Bild auch sehen kann. Das ist allerdings nicht der Fall für das Gleichungssystem C. Da laufen die Darstellungen der Funktionen im Koordinatensystem (die Geraden sind) parallel zueinander, sie treffen einander nie. Sie haben daher keinen gemeinsamen Punkt und das Gleichungssystem hat daher keine Lösung (man sagt, dass die Lösung die leere Menge ist). Im Gleichungssystem D hingegen sind alle Punkte der einen Funktion auch Punkte der anderen. Alle Wertepaare, die zu diesen Funktionen gehören, sind daher auch Lösungen des Gleichungssystems D. Das System hat somit unendlich viele Lösungen. Beide Funktionen sind in diesem Fall unterschiedliche Darstellungen der gleichen Funktion. Tatsächlich, wenn man beide Seiten der zweiten Funktion (des Systems D) durch 3 dividiert, bekommt man die erste Funktion:
.
Lösbarkeit eines linearen Gleichungssystems mit 2 Variablen
[Bearbeiten]Man soll zuerst beide Gleichungen in die sogenannte explizite Form umformen, also in der Form, in der y allein auf der linken Seite steht. Nehmen wir die Gleichungssysteme A, C und D des vorherigen Absatzes:
| Gleichungssystem A | Gleichungssystem C | Gleichungssystem D | ||
|---|---|---|---|---|
In der expliziten Form sehen diese Systeme wie im Folgenden aus:
| Gleichungssystem A | Gleichungssystem C | Gleichungssystem D | ||
|---|---|---|---|---|
Bei System A ist die Steigung unterschiedlich (-1 in der ersten Gleichung und -0,6 in der zweiten).
Wenn die Steigung der beiden linearen Funktionen unterschiedlich ist, dann hat das System mit Sicherheit genau eine Lösung.
Bei den Systemen C und D ist die Steigung überall die Gleiche (). Im System C haben die Gleichungen einen anderen y-Achsenabschnitt (+4 und +2). Im System D ist hingegen auch der y-Achsenabschnitt der beiden Gleichungen der gleiche (+4)
Wenn die Steigung der beiden linearen Funktionen die gleiche ist, gibt es zwei Möglichkeiten:
- Ist der y-Achsenabschnitt unterschiedlich, dann gibt es keine Lösung.
- Ist der y-Achsenabschnitt der gleiche, dann gibt es unendlich viele Lösungen.
Textaufgaben linearer Gleichungssysteme mit 2 Variablen
[Bearbeiten]In einem Café gibt es 8 Tische. Manche sind für 3 Personen und der Rest für 5 Personen. Insgesamt kann das Café 36 Personen bedienen. Wie viele 3 bzw. 5 Personen-Tische gibt es im Café?
Schauen wir die Denkweise genauer an. Die Anzahl der Tische ist bekannt, als auch die der Personen insgesamt. Was ist hier unbekannt (und letztendlich auch gefragt)? Wie viele Tische für 5 Personen und wie viele für 3 Personen es gibt. Für die Unbekannten in jedem mathematischem Problem benutzt man irgendwelche Symbole. Wir haben x und y benutzt, dass könnte aber genauso a und b, oder m und n, oder f und d oder irgendwas anders sein. Wichtig: Es gibt zwei Unbekannte, wir müssen also zwei verschiedenen Symbole dafür benutzen. Wenn es drei Unbekannte gibt, dann soll mal drei unterschiedlichen Symbole benutzen usw. (wie werden uns aber hier nur mit Gleichungssystemen mit zwei Unbekannten beschäftigen).
Am Anfang muss man definieren, was jedes Symbol darstellt. In dieser Aufgabe haben wir gesagt, dass die Tische für 3 Personen und y die Tische für 5 Personen sind:
x: die Tische für 3 Personen
y: die Tische für 5 Personen
Dieser Schritt sollte nicht so schwer sein. Man gibt einfach Namen (Symbole) für die unbekannten Sachen. Beim nächsten Schritt haben viele Menschen die größten Schwierigkeiten. Dabei ist die Sache nicht wirklich so schwer. Man soll das Problem vorsichtig lesen und den Text in die mathematische Sprache umsetzen. Dafür muss man nicht den ganzen Text verstehen, sondern auf Schlüsselworte beachten. In dieser Aufgabe steht, dass es 8 Tische gibt. Auch wenn man nicht wüsste, was ein Tisch ist, kann man schon schreiben, dass die Tische zusammen 8 sind. Welche Rechenart steht in Mathematik für zusammen? Die Addition. Also:
x+y=8
Wir haben zwei Unbekannte, also wir brauchen zwei Gleichungen, um die Aufgabe eindeutig zu lösen. Die zweite Gleichung zu erzeugen war in dieser Aufgabe nicht so leicht. Wir haben gesagt: Wenn es 2 Tische für 3 Personen gibt, dann sitzen an diesen Tischen 2⋅3=6 Personen, es 5 Tische für 3 Personen gibt, dann sitzen an diesen Tischen 5⋅3=15 Personen usw. Man merkt, dass damit wir die Personen berechnen, die Anzahl der Tische mit der Anzahl der Personen pro Tisch (hier 3 Personen pro Tisch) multiplizieren müssen. Wir wissen aber nicht, wie viele Tische für drei Personen es gibt. Wir haben aber doch ein Symbol dafür benutzt: das sind x Tische. Dieses Symbol muss man also mit der Anzahl der Personen pro Tisch (hier 3) multiplizieren, um durch einen Term zu zeigen, wie viele Personen an diesen Tischen sitzen können: 3x! Dass ist (noch) nicht eine bestimmte Zahl, das sind aber doch die Personen die an diesen x Tischen sitzen können. Entsprechend können an den y Tischen für 5 Personen insgesamt 5y Personen sitzen (Anzahl der Tische y mal Personen pro Tisch, hier 5). In der Aufgabe steht, dass das Café insgesamt 36 Personen bedienen kann. Also die Anzahl der Personen, die an den zwei Tischkategorien (eine Kategorie die 3-Personen Tische, zweite Kategorie die 5-Personen Tische) sitzen können ist insgesamt 36 Personen. Welche Rechenart wird hier angedeutet? Wieder Addition. Die Personen der beiden Kategorien zusammen (also plus) sind 36:
3x+5y=36
Wir haben also zwei Gleichungen und zwei Unbekannte.
x+y=8
3x+5y=36
Jetzt kann man eine der dargestellten Wege benutzen, um x und y herauszufinden. In unserem Beispiel haben wir das Ersetzungsverfahren benutzt.
Erzeugen wir das Gleichungssystem für noch ein paar Textaufgaben:
Iris ist 2,5 mal älter als ihr Bruder Andreas. Zusammengezählt sind ihre Altersjahren 14. Wie viele Jahren alt sind die beiden Geschwister?
Gefragt sind die Lebensalter der beiden Geschwister. Wir schreiben mit i das Lebensalter von Iris und mit a von Andreas. Iris ist 2,5 mal älter und zusammen sind die Jahre 18:
i=2,5⋅a und i+a=14
Dieses System lässt sich sehr leicht durch das Ersetzungsverfahren lösen. Wir ersetzen i in der zweiten Gleichung durch 2,5a (da i=2,5a, wie es schon in der ersten Gleichung steht):
i+a=18 → 2,5a+a=14 → 3,5a=14 (:3,5) → a=4 und sofort i=2,5a=2,5⋅4 → i=10 (also tatsächlich i+a=14)
Die Summe des Fünffachen einer Zahl und 4 ist so viel wie eine andere Zahl um 1 reduziert. Die Differenz des dreifachen der zweiten Zahl und 43 ist so viel wie die erste Zahl um 14 erhöht. Berechnen sie die Zahlen.
Viele finden solche Aufgaben extrem schwer. Dabei muss man einfach Schritt für Schritt vorgehen. Erst gibt man Symbole für die zwei unbekannten Zahlen.
e ist die erste Zahl
z ist die zweite Zahl
Gehen wir Schritt für Schritt vor:
Die Summe des Fünffachen einer Zahl.... Die erste Zahl haben wir e genannt. Das fünffache bedeutet 5e. Über die Summe wissen wir noch nichts, außer dass der erste Summand 5e sein wird.
Die Summe des Fünffachen einer Zahl und 4.... Hier erkennen wir den zweiten Summand: 4. Also bisher haben wir: 5e+4
Die Summe des Fünffachen einer Zahl und 4 ist so viel wie.... ...ist so viel wie in der mathematische Sprache umgesetzt ist nichts mehr und nichts mehr als das Symbol für gleich (=). Also bisher haben wir: 5e+4=
Die Summe des Fünffachen einer Zahl und 4 ist so viel wie eine andere Zahl um 1 reduziert. Die zweite (die "andere") Zahl haben wir z genannt und sie wird um 1 reduziert also z−1. Bisher haben wir: 5e+4=z−1 Hier endet der erster Satz. Wir haben also schon unsere erste Gleichung!
5e+4=z-1
Fangen wir jetzt mit dem zweiten Satz an: Die Differenz des dreifachen der zweiten Zahl.... Über die Differenz kenne wir nur den Minuend. Er ist das dreifache der zweiten Zahl. Die zweite Zahl haben wir z genannt, also ist ihr Dreifaches 3z. Bisher haben wir daher: 3z−...
Die Differenz des dreifachen der zweiten Zahl und 43 Jetzt haben wir auch den Subtrahend der Differenz: 3z−43
Die Differenz des dreifachen der zweiten Zahl und 43 ist so viel wie ...ist so viel wie bedeutet ist gleich: 3z−43=
Die Differenz des dreifachen der zweiten Zahl und 43 ist so viel wie die erste Zahl um 14 erhöht Die erste Zahl ist e und sie wird um 14 erhöht (also plus 14): 3z−43=e+14. Wir haben jetzt auch die zweite Gleichung! Das Gleichungssystem lautet:
5e+4=z−1
3z−43=e+14
Dieses System kann man dann mit einem der präsentierten Verfahren lösen. Die Antwort ist e=3 und z=20, wie man überprüfen kann:
5⋅3+4=20−1 ✔ und
3⋅20−43=3+14 ✔
Viele Menschen denken, dass solche Aufgaben schwer wären. Wie man hier sieht, wenn man die Aufgabe Schritt für Schritt löst, ist es nicht so schwer. Das braucht einfach etwas Konzentration, ist aber durchaus fast für jeden möglich.
In einer Flups gibt es 37 Tröpats. Manch davon haben 4 Hupals, die restlichen 7 Hupals. Die Flups beihaltet damit 190 Hupals. Wie viele Tröpats mit 4 bzw. 7 Hupals gibt es?
Man mag hier fragen, was zum Teufel Flups, Tröpats und Hupals sind. Meine Antwort ist dann eine weitere Frage: Ist diese Kenntnis für die Lösung der Aufgabe notwendig? Die Antwort ist ganz einfach NEIN! Wenn in einer Prüfungssituation jemand eine unbekanntes Wort trifft, soll man erst entscheiden, ob dieses Wort für die Lösung wichtig ist, sonst verliert man Zeit, die für eine Prüfung i.d.R. sehr wichtig ist. Ziel dieser Aufgabe ist darauf aufmerksam zu machen. In der Aufgabe wird NICHT gefragt, was Flups usw sind. Ḿan braucht es daher auch nicht wissen. Wichtig sind nur Schlüsselworte und -phrasen, wie z.B. In... gibt es, was darauf hinweist, dass die Tröpats insgesamt 37 sind. Der erste Schritt ist für jede Unbekannte ein Symbol einzusetzen. Wenn v die Tröpats mit 4 Hupals sind und s die Tröpats mit 7 Hupals, dann haben wir die erste und die zweite Gleichung, genau wie im ersten Beispiel in diesem Teilkapitel:
v+s=37
4v+7s=190
Das System kann man dann in einer beliebige Weise lösen. Die Antwort ist 23 Tröpats mit 4 Hupals und 14 Tröpats mit 7 Hupals (was das auch immer sein könnte ![]() ).
).
Trigonometrische Funktionen
[Bearbeiten]Definition von Sinus Kosinus und Tangens
[Bearbeiten]
| Definitionen |
Trigon. Umkehrf. |
| Pythagoras abstrakt |
Pythagoras konkret |


An jedem rechtwinkeligen Dreieck gilt eine gewisse Regel, die schon seit zumindest 4000 Jahren bekannt ist. Diese Regel wurde nach einem griechischen Philosophen genannt: der Pythagoräische Lehrsatz.
In einem rechtwinkeligem Dreieck ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.
Dieser Satz ist verständlicher, wenn wir das erste Dreieck für einen Entwurf des Satzes mit Symbolen benutzen. Wenn a und b die zwei kleineren Seiten des rechtwinkeligen Dreiecks (Katheten genannt) und c die größere (Hypotenuse genannt) sind, ist der entsprechende mathematische Ausdruck:
Genauso seit tausenden Jahren bekannt ist eine andere Eigenschaft der geometrischen Figuren und in diesem Fall der rechtwinkeligen Dreiecke. Bei ähnlichen Dreiecken (wenn alle Winkel gleich sind) ist das Verhältnis (der Bruch der Längen) der entsprechenden Seiten konstant. im ersten Dreieck im Bild ist genauso viel wie im zweiten. Besonders in rechtwinkeligen Dreiecken bedeutet diese Tatsache, dass:
- Das Verhältnis der dem kleinsten Winkel gegenüberliegenden Seite (hier a) zu Hypotenuse (hier c) eine konstante Zahl für alle ähnlichen rechtwinkeligen Dreiecke ist.
- Das Verhältnis der dem kleinsten Winkel anliegenden Kathete (hier b) zu Hypotenuse eine konstante Zahl für alle ähnlichen rechtwinkeligen Dreiecke ist.
Das entsprechende gilt für den anderen nicht rechten Winkel.
Mit Buchstaben ist dieser Satz viel verständlicher. Im ersten Dreieck gilt: und sind konstant, für alle ähnlichen rechtwinkeligen Dreiecke.
Der erste Bruch wurde Sinus genannt, der zweite Kosinus. Für den kleinsten Winkel (nennen wir ihn ) des ersten Bildes gilt also:
und
Die zwei Dreiecke im Bild sind ähnlich. Die kleinste Kathete a im ersten Dreieck durch seine Hypotenuse, wird so viel sein, wie die kleinste Kathete c im zweiten Dreieck durch seine Hypotenuse:
und
Somit werden Sinus und Kosinus definiert. Sinus und Kosinus sind die zwei wichtigsten trigonometrischen Funktionen. Formell:
|
und |
|
wobei irgendein nicht rechter Winkel |
Für den anderen nicht rechten Winkel des ersten Dreiecks (nennen wir ihn ) gilt dann:
und ,
da gegenüber von die Seite b ist.
Alle Winkel zusammen in einem Dreieck sind 180°. In einem rechtwinkeligen Dreieck ist einer Winkel 90°, daher sind die anderen zwei zusammen auch 90°. Daher gilt:
und .
Mit Hilfe des Pythagoräischen Lehrsatzes ist auch leicht zu zeigen, dass:
.
und bedeuten bzw. .
Es gibt allerdings noch eine wichtige Trigonometrische Funktion, der Tangens. Er ist das Verhältnis der Gegen- zu Ankathete:
Die Symbole für manche weiteren trigonometrischen Funktionen sind: und . Es gibt allerdings auch die Umkehrfunktionen. Von und werden sie mit den Symbolen bzw. oder bzw. (besonders bei Taschenrechnern) dargestellt.
Radiant
[Bearbeiten]Für die Messung einer Drehbewegung verwenden wir in der Regel den Winkelgrad. Ein Grad ist einer ganzen Drehung. Eine ganze Drehung ist damit 360°. Bei Rechnungen in der höheren Mathematik und in der Physik hat sich allerdings gezeigt, dass eine andere Einheit notwendig ist, der Radiant (rad). Eine ganze Drehung ist rad. Mit Schlussrechnung können wir daher sehr einfach zwischen den beiden Einheiten [2]umrechnen:
- ↑ BIPM – SI prefixes (englisch) – „BIPM – SI-Broschüre“, 8. Auflage, März 2006, Abschnitt 3.1: SI-Präfixe
- ↑ (die allerdings dimensionslos sind)
Sinus und Kosinussatz
[Bearbeiten]Beweis des Sinussatzes
[Bearbeiten]Der Sinussatz besagt, dass in jedem Dreieck die Verhältnisse der Sinusse seiner Winkeln zur entsprechenden gegenüberliegenden Seiten gleich zueinander sind:
Selbstverständlich gilt der Satz auch für die Kehrwerte:
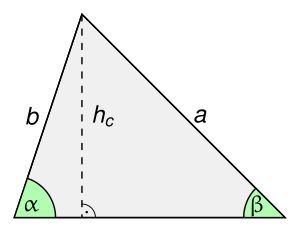
Um den Satz für zwei zufällige Winkel des Dreiecks zu beweisen, reicht es eine Höhe (im Bild die Höhe ) des Dreiecks einzuzeichnen.[1] Diese Höhe zerlegt das Dreieck in zwei rechtwinklige Teildreiecke, in denen man den Sinus von und jeweils als Quotient von Gegenkathete und Hypotenuse ausdrücken kann, nach der Definition von Sinus:
Auflösen nach ergibt:
Durch Gleichsetzen erhält man demnach
Dividiert man nun durch , so erhält man den ersten Teil der Behauptung:
Die Gleichheit mit ergibt sich entsprechend durch Benutzung der Höhe oder .
Beweis des Kosinussatzes
[Bearbeiten]Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras auf alle Dreiecke. Der besagt, dass das Quadrat von jeder Seite eines zufälligen Dreiecks gleich die Differenz der Summe der Quadrate der anderen zwei Seiten minus das zweifache des Produktes dieser Seiten und des Kosinus der dazwischen liegenden Winkel ist:
Da die Seite c zufällig ausgewählt wird, gilt der Satz auch für die anderen zwei Seiten:
Im folgenden Beweis wird vorausgesetzt.

In den Teildreiecken soll der Satz des Pythagoras angewandt werden, um einen Rechenausdruck für zu finden. Wir zeichnen wieder die Höhe ein. Für das rechte (rechtwinkelige) Dreieck gilt laut Satz von Pythagoras:
Die Seite wird allerdings in der Figur in zwei Teile zerlegt, es gilt daher
Für das linke (auch rechtwinkelige) Dreieck gilt daher:
(nach der binomischen Formel)
Kombinieren wir diese drei Gleichungen, ergibt sich für :
Zusätzlich gilt laut Definition des Kosinus:
Wenn wir dieses Ergebnis in die letzten Gleichung für einsetzten, ergibt sich der Kosinussatz:
Für muss der Beweis geringfügig modifiziert werden. Für ergibt sich der Kosinussatz direkt aus dem Satz des Pythagoras.
Direkte Anwendung des Sinus und des Kosinussatzes
[Bearbeiten]
- Berechnen sie die Diagonalen des abgebildeten Deltoids, wenn die Seite 4,3 cm, die Seite 7,6 cm und der dazwischen liegende Winkel 134° sind.
Mit direkter Anwendung des Kosinussatzes können wir die Diagonale sofort berechnen:
Mit Hilfe des Sinussatzes können wir dann den Winkel berechnen:
Dann können wir auch die andere Diagonale mit Hilfe der Definition von Sinus berechnen:
Vermessungsaufgaben
[Bearbeiten]- Lisa beobachtet die Antenne auf dem Dach eines Gebäudes. Ihre Augen sind 1,73 m hoch, die Antenne selber ist 2,8 m hoch. Den unteren Rand der Antenne sieht Lisa unter einem Höhenwinkel von 67°, den oberen unter 74°. Wie weit vom Gebäude (genauer: vom "Fuß" der Antenne) befindet sich Lisa und wie hoch ist das Gebäude? Machen Sie eine saubere Skizze für die Berechnung!

Der Winkel ist , der Winkel . Da ein rechtwinkeliges Dreieck ist, ist der Winkel . Mit Hilfe des Sinussatzes können wir dann die Seite berechnen:
.
Mit Hilfe der Definition von Sinus und Kosinus können wir dann die Fragen beantworten:
Höhe des Gebäudes:
Abstand:
- Vom Gipfel eines 1563 m hohen Berges wird der Abstand zwischen zwei Türmen in einem Tal gemessen, die sich beide auf einer Höhe von 548 m befinden. Zum ersten Turm wird der Tiefenwinkel gemessen und nach Schwenken des Messgerätes um den Horizontalwinkel zum anderen Turm wird dieser unter dem Tiefenwinkel gesehen. Wie viel ist der Abstand zwischen den Türmen? Machen Sie eine saubere Skizze für die Berechnung!

Die Strecke ist der Höhenunterschied, also . Mit Hilfe der Definition von Tangens können wir leicht die Strecken messen:
.
.
Mit Hilfe des Kosinussatzes können wir dann den Abstand zwischen den beiden Türmen berechnen:
Vektoren
[Bearbeiten]Vektorielle und skalare Größen
[Bearbeiten]Die Größen, die bei ihrer vollständigen Beschreibung auch die Angabe einer Richtung brauchen, nennt man Vektoren. Solche vektrorielle Größen sind die Strecke, die Geschwindigkeit, die Beschleunigung und die Kraft.
Die Größen ohne Richtung im Raum, wie die Zeit, die Masse, die Energie, die Arbeit, die Leistung und den Wirkungsgrad, nennt man Skalare.
Vektor und Punkt
[Bearbeiten]

Ein Punkt ist zwar eine Konstruktion der Phantasie, man kann ihn aber doch in einem Koordinatensystem darstellen. Die Schreibweise eines Punktes mit den Koordinaten und ist oder auch , wobei immer erst die x- und dann die y-Koordinate geschrieben wird. Oft schreibt man auch Strichpunkte (Semikolons) anstelle der Kommata, um Missverständnisse mit Dezimalzahlen zu vermeiden. Um die Position des Punktes im Koordinatensystem zu finden, geht man aus dem Koordinatenursprung rechts so oft wie der x-Wert (links, wenn der x-Wert negativ ist) und nach oben so oft wie der y-Wert (nach unten, wenn der y-Wert negativ ist) angibt. Im Bild 1 z. B. sieht man den Punkt , also 5 Einheiten rechts vom und 3 Einheiten oberhalb des Ursprungs und den Punkt , also 4 Einheiten links (weil der x-Wert negativ ist, also -4) und 2 Einheiten oberhalb. Den idealen dimensionslosen Punkt stellt man im Koordinatensystem eben mit einem Punkt, der doch Dimensionen hat, also mit einem kleinen Kreis oder manchmal auch mit einem kleinen Rhobus usw. dar. Für Punkte im Raum (drei Dimensionen) schreibt man drei Zahlen nebeneinander, die der Reihe nach die x-, y- und z-Koordinate angeben: oder auch .


Ein Vektor ist ein Pfeil im Raum. Einen Vektor schreibt man als Zahlen nebeneinander oder untereinander , wobei wieder erst (links bzw. oben) die x- und dann (rechts bzw. unten) die y-Koordinate geschrieben wird. Der Unterschied in der Schreibweise zum Punkt ist, dass man in der Regel für Punkte einen großen und für Vektoren einen kleinen Buchstabe mit einem Pfeil darüber benutzt, das ist aber nicht immer so.
Im Bild 2 fängt der Vektor am Punkt an. Man geht 3 Einheiten rechts und 4 nach oben (wie bei einem Punkt) und man gelangt an den Punkt . Der Pfeil fängt also am Punkt an und endet am Punkt . Wenn wir vom Punkt P2 den Punkt P1 subtrahieren, wenn wir also die x-Koordinate des Punkts P1 (1) aus der x-Koordinate des Punkts P2 (4) subtrahieren (4-1=3) bekommen wir die x-Koordinate des Vektors zwischen P1 und P2. Wenn wir die y-Koordinate des Punkts P1 (2) aus der y-Koordinate des Punkts P2 (6) subtrahieren (6-2=4) bekommen wir die y-Koordinate des Vektors zwischen P1 und P2 (4). Dieser Vektor ist tatsächlich der Vektor .

Ein Vektor ist aber in der Regel nicht an einem Punkt gebunden. Im Bild 3 wurde der Vektor v verschoben, er fängt am Punkt an und endet am Punkt . Wenn wir hier wieder die entsprechenden Koordinaten der Punkte P4 und P3 subtrahieren, also 2-(-1)=3 für die x-Koordinate und 3-(-1)=4 für die y-Koordinate, bekommen wieder den Vektor .

Im Bild 4 sieht man, dass tatsächlich zwischen den Punkten P1 und P2 einerseits und den Punkten P3 und P4 andererseits der gleiche Vektor v liegt.
Einen Punkt kann man auch mit sogenannten Ortsvektoren darstellen. Diese sind zwar als Vektoren dargestellt sind aber doch an einem Punkt, nämlich den Koordinatenursprung, gebunden, wie im Bild 5.
Der Unterschied also zwischen Punkt und Vektor ist:
Ein Punkt ist an den Koordinatenursprung gebunden, ein Vektor ist nicht unbedingt an einen Punkt gebunden.
Vektoraddition
[Bearbeiten]
Wenn wir zwei Vektoren addieren wollen, addieren wir die x-Koordinate des ersten Vektors zur x-Koordinate des zweiten. So bekommen wir die x-Koordinate der Summe der beiden Vektoren. Dann addieren wir die y-Koordinate des ersten Vektors zur y-Koordinate des zweiten. So bekommen wir die y-Koordinate der Summe der beiden Vektoren.
Im Bild 1 fängt der Vektor u beim Koordinatenursprung und endet 4 Einheiten rechts (x-Koordinate) und 6 nach oben (y-Koordinate) also ist . Der Vektor v fängt am Punkt (4|6) und endet 1 Einheit nach rechts und drei nach unten, am Punkt (5|3), also ist . Wenn wir einerseits die x-Koordinate des Vektors u zur x-Koordinate des Vektors v addieren (4+1=5) und andererseits die y-Koordinate des Vektors u zur y-Koordinate des Vektors v (6-3=3), bekommen wir die entsprechenden Koordinaten der Summe der Vektoren u+v, also ist .


Wenn jemand jetzt aus dem Vektor u den Vektor v subtrahieren will, dann soll man zum Vektor u den Gegenvektor von nämlich den Vektor addieren. Dass der Vektor tatsächlich der Gegenvektor von v ist, kann man im Bild 2 klar sehen (gleicher Vektor in die Gegenrichtung). Das Ergebnis w von u-v sieht man im Bild 3. Tatsächlich ist die x-Koordinate von w die x-Koordinate von u minus die x-Koordinate von v (4-1=3) und die y-Koordinate von w die x-Koordinate von u minus die y-Koordinate von v (6-(-3)=9).


Rein theoretisch könnte man Vektoren ohne Koordinatensystem darstellen und subtrahieren (Bild 4,5: ) oder addieren (Bild 6), in diesem Fall ist es aber nicht klar, welche die x und welche die y Richtung ist und vor allem, welche die Einheit ist! Daher ist es immer notwendig ein Koordinatensystem anzugeben.


Um Vektoren zu addieren, kann man auch ein Parallelogramm benutzen, wie im Bild 7. Dieser Vorgang ist aber aufwendiger, wenn man mehrere Vektoren addieren bzw. subtrahieren will (wie im Bild 6).
Vektor mit Zahl multiplizieren
[Bearbeiten]



Man kann einen Vektor mit einer Zahl multiplizieren. In den Bildern 1 und 2 sieht man das Doppelte bzw. das Dreifache eines Vektors, obwohl hier keine Einheiten oder Achsen gegeben sind. Im Bild 3 sieht man sowohl das Doppelte als auch den Gegenvektor .
Wie multipliziert man eine Zahl mit einem Vektor rechnerisch? Man multipliziert jede Koordinate des Vektors mit der Zahl. Wie man im Bild 4 ablesen kann, ist der Vektor durch die Koordinaten des Vektors je multipliziert mit -1:
Für den Vektor multipliziert man jede Koordinate des Vektors mit 2:
Entsprechend ist es bei den anderen Vektoren:
In der Physik gibt es zwei Arten von Größen: Skalare (z.B. Masse, Zeit, Energie) und Vektoren (z.B. Strecke, Geschwindigkeit, Beschleunigung, Kraft). Wenn man ein Skalar mit einem Vektor multipliziert (z.B. Masse mal Beschleunigung) ist das Ergebnis ein Vektor (in diesem Fall Kraft), dessen Koordinaten wie in diesem Absatz berechnet werden (also Zahl mal jede Koordinate des Vektors).
Betrag eines Vektors
[Bearbeiten]
Der Betrag eines Vektors ist nichts mehr und nichts weniger als seine Länge. Wie man aus dem Bild ablesen kann, kann man die Länge mit Hilfe des Satzes von Pythagoras berechnen. Die Seite a des Rechtwinkeligen Dreiecks ABC ist die y-Koordinate a = uy = 4 des Vektors (die untere Zahl) und die Seite b die x-Koordinate b=ux=3 (die obere Zahl). Daher ist die Länge des Vektors .
Der Gegenvektor hat genau die gleiche Länge, also den gleichen Betrag: .
Richtung eines Vektors und Steigung
[Bearbeiten]

Die Richtung eines zweidimensionalen Vektors hat stark mit der Steigung einer linearen Funktion zu tun. Wenn man von einem Punkt ausgeht und wissen will, in welcher Richtung der Vektor gezeichnet werden muss, kann man einen Schritt nach rechts parallel zur x-Achse machen und dann genau so viel auf der y-Achse, wie die y-Koordinate (untere Zahl) durch die x-Koordinate (obere Zahl).
Eine Darstellung einer Gerade ist auch die „Punkt-Vektor“ Darstellung. In dieser Darstellung der Gerade ist ihre Steigung genau die y-Koordinate (untere Zahl) durch die x-Koordinate (obere Zahl) des Vektors. In so einem Fall wäre die Steigung der entsprechenden Gerade für den Vektor im Bild 1 gleich und im Bild 2 gleich
Orts- und Richtungsvektoren
[Bearbeiten]Wie im Abschnitt über Vektor und Punkt erklärt, kann man einen Punkt auch durch einen vom Koordinatenursprung ausgehenden Vektor darstellen. So einen Vektor nennt man „Ortsvektor“. Um einen Ortsvektor von den anderen Vektoren zu unterscheiden, benutzt man für die anderen, nicht am Koordinatenursprung gebundenen Vektoren den Name „Richtungsvektor“. Wenn man aber das Wort „Vektor“ ohne weitere Bezeichnungen benutzt, ist ein Richtungsvektor gemeint.
Orts- und Richtungsvektoren
[Bearbeiten]Zerlegung eines Vektors zu seinen Komponenten
[Bearbeiten]Einen Vektor kann man zu sogenannten Komponenten zerlegen. Das ist quasi das Gegenteil von Vektoren addieren. Man wählt ein Koordinatensystem (zwei Richtungen auf der Ebene, in der Regel senkrecht zueinander) und findet zwei Vektoren, einen auf jede Achse des Koordinatensystems, dessen Summe der Anfangsvektor ist.



Das Bezugssystem muss aber nicht unbedingt Achsen, die normal aufeinander stehen sein. Das ist der Fall im Bild 3. Hier gelten aber vorherigen Gleichung nicht mehr.
Skalarprodukt von Vektoren
[Bearbeiten]Von den vier Grundrechenarten sind zwischen Vektoren nur drei möglich, die Strichrechnungen (Addition, Subtraktion) und die Multiplikation. Dafür gibt es allerdings zwei Arten von Multiplikation zwischen Vektoren, die sogenannten Skalar- und Kreuzprodukt. Hier werden wir uns mit dem Skalarprodukt beschäftigen, das durch den Punkt der gewöhnlichen Multiplikation dargestellt wird[1]. Es kann zwischen nur zwei Vektoren stattfinden und wird durch die Summe der Produkte der einzelnen Koordinaten der Vektoren berechnet. Das bedeutet: Wenn wir das Skalarprodukt der Vektoren und berechnen wollen, müssen wir die x-Koordinate des Vektors mit der x-Koordinate des Vektors multiplizieren, die y-Koordinate des Vektors mit der y-Koordinate des Vektors auch multiplizieren und die Ergebnisse zusammenrechnen:
Hier ein konkretes Beispiel:
Wir sehen klar: Das Ergebnis eines Skalarproduktes zwischen Vektoren ist kein Vektor mehr, sondern eine Zahl.[2]
- ↑ für das Kreuzprodukt hingegen wird das Symbol benutzt
- ↑ Beim Kreuzprodukt hingegen ist das Ergebnis ein neuer Vektor
Winkelmaß zwischen zwei Vektoren
[Bearbeiten]Der Kosinus des Winkels zwischen zwei Vektoren lässt sich durch folgende Formel berechnen:
Im Zähler steht das Skalarprodukt der beiden Vektoren, im Nenner das Produkt ihrer Beträge. Diese Formel kann man mit Hilfe des Satzes von Pythagoras und der Definition des Kosinus in einem rechtwinkeligen Dreieck zeigen. Der Winkel lässt sich dann leicht mit Hilfe der Umkehrfunktion von Kosinus berechnen:
Hier ein konkretes Beispiel:


































































































































![{\displaystyle \textstyle a^{1 \over m}={\sqrt[{m}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fea6f5273a124a9040ac9a26a48c1b641b2fee32)
![{\displaystyle {\begin{aligned}{\sqrt {a}}&=b&&\rightarrow \quad a=b^{2}\\{\sqrt[{-5}]{m}}&=n&&\rightarrow \quad m=n^{-5}\\{\sqrt[{4,3}]{m}}&=n&&\rightarrow \quad m=n^{4,3}\\{\sqrt[{\sqrt {6}}]{x}}&=z&&\rightarrow \quad x=z^{\sqrt {6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e817daca16798c8dce8f4260b45ac53419d7b8f)
![{\displaystyle {\sqrt[{m}]{a}}=b\quad \rightarrow \quad a=b^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5e730a5129a881eaff79b220dc1a6ea326ed54)



![{\displaystyle ({\sqrt[{n}]{a}})^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84e72f3f41f93d141f4e8df331367846c1b3c856)









![{\displaystyle ({\sqrt[{n}]{a}})^{n}={(a^{1 \over n})}^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98f416c685cc71862c3aad3f9e3d909444904823)
![{\displaystyle {\sqrt[{n}]{a}}=a^{1 \over n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb00d02a7cdd73d845e32f7a648aa75e297e93d)
![{\displaystyle {\sqrt[{m}]{a^{n}}}=({\sqrt[{m}]{a}})^{n}=a^{n \over m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6419cb1b8600ea98519e7c274a6a091d06c5b22)
![{\displaystyle {\sqrt[{n}]{a^{n}}}=({\sqrt[{n}]{a}})^{n}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af274240c4278adde49b27adf3aec8844f4fadbb)
![{\displaystyle a^{1 \over m}={\sqrt[{m}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81b4d6953524a07958bc266d9659c2af38fa4730)
![{\displaystyle {\left({\sqrt[{35}]{w^{-5}}}\right)}^{-14}={\left[{(w^{-5})}^{1 \over 35}\right]}^{-14}=w^{(-5)\cdot {1 \over 35}\cdot {(-14)}}=w^{70 \over 35}=w^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09d003e6edb8db67f9b6539e446c9c7052c0f7dc)
![{\displaystyle {\left({\sqrt[{35}]{w^{-5}}}\right)}^{-14}={\left[{(w^{-5})}^{1 \over 35}\right]}^{-14}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/946b53d72917eb518fc6703a71c3b1d40f11a248)

![{\displaystyle {\left[{(w^{-5})}^{1 \over 35}\right]}^{-14}=w^{(-5)\cdot {1 \over 35}\cdot {(-14)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/984f233022bc759bf4fcec545b6c3a0276e22463)


![{\displaystyle {\left(b^{3 \over 7}\right)}^{28 \over 9}=b^{{\frac {3}{7}}\cdot {\frac {28}{9}}}=b^{\frac {4}{3}}\left(={\sqrt[{3}]{b^{4}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b78068f1ad9bc755f945b02959c02dd1a14c7476)
![{\displaystyle \left(\left(b^{3 \over 5}\right)^{3}\cdot {\sqrt[{5}]{b^{6}}}\cdot b^{-2}\right)^{29}=\left(b^{{\frac {3}{5}}\cdot 3}\cdot {b^{6 \over 5}}\cdot b^{-2}\right)^{29}=\left(b^{{\frac {9}{5}}+{\frac {6}{5}}-2}\right)^{29}=\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/97585b67800a1cf4001bdbd1740e03a7676001a4)

![{\displaystyle \left(\left(b^{3 \over 5}\right)^{3}\cdot {\sqrt[{5}]{b^{6}}}\cdot b^{-2}\right)^{29}=\left(b^{{\frac {3}{5}}\cdot 3}\cdot {b^{6 \over 5}}\cdot b^{-2}\right)^{29}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dda6c22b695620816cd53096fdee0a6f60554e1)



![{\displaystyle {\dfrac {\sqrt[{3}]{{\Bigl (}b^{15 \over 7}{\Bigr )}^{28}}}{b^{3} \over b^{-8}}}={\frac {\left(b^{\frac {15}{7}}\right)^{28 \over 3}}{b^{3-(-8)}}}={\frac {b^{{\frac {15}{7}}\cdot {\frac {28}{3}}}}{b^{3+8}}}={\frac {b^{20}}{b^{11}}}=b^{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ad337a347bc7a74f1ca8e8f230490838fd06c34)
![{\displaystyle {\sqrt[{3}]{{\Bigl (}b^{15 \over 7}{\Bigr )}^{28}}}={\left(b^{\frac {15}{7}}\right)^{28 \over 3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0da10f6a4e890d81881d5b5bfc7b7fa0d9893311)




























































































![{\displaystyle {\boldsymbol {m}}={\frac {2\cdot c_{L}\cdot k_{B}\cdot T\cdot d}{[d\cdot (2{,}2-a)+l]\cdot v^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8df884a41b99e6f4f04586aa26a1e15fafc78d86)