Ing Mathematik: Flächen

Zurück zu Raumkurven | Hoch zu Gesamtinhaltsverzeichnis | Vor zu Linienintegrale

Allgemeines

• implizite Form: $F(x,y,z)={\text{konst.}}$
• explizite Form: $z=f(x,y)$
• Parameterdarstellung: $x=x(u,v);\;y=y(u,v);\;z=z(u,v)$

Flächen sind hier 2-dimensionale Elemente im 3-dimensionalen Raum.

Grundformen der Flächentheorie

1. Grundform

Es gilt $\mathrm {d} s=|\mathrm {d} \mathbf {r} |$.

$\mathrm {d} s^{2}=(\mathrm {d} \mathbf {r} )^{2}=\left({\frac {\partial \mathbf {r} }{\partial u}}\mathrm {d} u+{\frac {\partial \mathbf {r} }{\partial v}}\mathrm {d} v\right)^{2}=\underbrace {\left({\frac {\partial \mathbf {r} }{\partial u}}\right)^{2}} _{E}\mathrm {d} u^{2}+2\underbrace {{\frac {\partial \mathbf {r} }{\partial u}}{\frac {\partial \mathbf {r} }{\partial v}}} _{F}\mathrm {d} u\mathrm {d} v+\underbrace {\left({\frac {\partial \mathbf {r} }{\partial v}}\right)^{2}} _{G}\mathrm {d} v^{2}$

Die erste Grundform der Flächentheorie lautet ($E,F,G$ sind die metrischen Koeffizienten, oder auch gaußsche Fundamentalgrößen):

$\mathrm {d} s^{2}=E\mathrm {d} u^{2}+2F\mathrm {d} u\mathrm {d} v+G\mathrm {d} v^{2}$

Es gilt auch:

$\mathrm {\dot {s}} ^{2}=E\mathrm {\dot {u}} ^{2}+2F{\dot {u}}{\dot {v}}+G{\dot {v}}^{2}$ und

$\mathrm {s} '^{2}=\left({\frac {\mathrm {d} s}{\mathrm {d} s}}\right)^{2}=Eu'^{2}+2Fu'v'+Gv'^{2}=1$.

Siehe auch  Erste Fundamentalform

2. Grundform

Die zweite Grundform beschäftigt sich mit den Krümmungsmaßen einer Fläche. Wir werden hier nicht näher darauf eingehen.

Siehe ggf. auch  Zweite Fundamentalform.

Tangentialebene

Totales Differenzial: $\mathrm {d} \mathbf {r} ={\frac {\partial \mathbf {r} }{\partial u}}\mathrm {d} u+{\frac {\partial \mathbf {r} }{\partial v}}\mathrm {d} v$

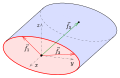
Tangentenvektor: $\mathrm {\mathbf {\dot {r}} } ={\frac {\partial \mathbf {r} }{\partial u}}{\dot {u}}+{\frac {\partial \mathbf {r} }{\partial v}}{\dot {v}}$

Dabei müssen ${\frac {\partial \mathbf {r} }{\partial u}}$ und ${\frac {\partial \mathbf {r} }{\partial v}}$ linear unabhängig voneinander sein, d.h. sie dürfen nicht parallel sein. Nur dann spannen sie eine Ebene (die Tangentialebene) auf.

Flächennormale

$\mathbf {N} ={\frac {{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}}{\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|}}$

Diese Einheitsnormale steht also immer senkrecht auf ${\frac {\partial \mathbf {r} }{\partial u}}$ und ${\frac {\partial \mathbf {r} }{\partial v}}$.

Flächenelement

Hier sei abgekürzt geschrieben $\mathbf {r} _{u}={\frac {\partial \mathbf {r} }{\partial u}}$ etc.

Das durch die Punkte ABCD aufgespannte Flächenelement lässt sich angenähert so schreiben

$\mathrm {d} \sigma =|\mathbf {r} _{u}\mathrm {d} u\times \mathbf {r} _{v}\mathrm {d} v|=|\mathbf {r} _{u}\mathrm {\times } \mathbf {r} _{v}\mathrm {|} \mathrm {d} u\mathrm {d} v$

Es gilt auch $|\mathbf {r} _{u}\times \mathbf {r} _{v}|^{2}=\mathbf {r} _{u}^{2}\mathbf {r} _{v}^{2}-(\mathbf {r} _{u}\mathbf {r} _{v})^{2}$

Für die Herleitung dieser Formel siehe die elementare Vektorrechnung (z.B.  Kreuzprodukt#Lagrange-Identität).

Somit ist $\mathrm {d} \sigma ={\sqrt {\mathbf {r} _{u}^{2}\mathbf {r} _{v}^{2}-(\mathbf {r} _{u}\mathbf {r} _{v})^{2}}}\mathrm {d} u\mathrm {d} v={\sqrt {EG-F^{2}}}\mathrm {d} u\mathrm {d} v$

Mit diesem Flächenelement lässt sich jetzt natürlich auch der Flächeninhalt berechnen:

$A=\iint _{F}\mathrm {d} \sigma =\int _{u=a}^{b}\int _{v=g(u)}^{h(u)}|\mathbf {r} _{u}\mathrm {\times } \mathbf {r} _{v}\mathrm {|} \mathrm {d} u\mathrm {d} v=\int _{u=a}^{b}\int _{v=g(u)}^{h(u)}{\sqrt {EG-F^{2}}}\mathrm {d} u\mathrm {d} v$

Beispiel: Berechnen wir einfach mal die Oberfläche einer Kugel. Es gilt (siehe Kugelkoordinaten)

$\mathbf {r} ={\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}\rho \cdot \sin \theta \cdot \cos \varphi \\\rho \cdot \sin \theta \cdot \sin \varphi \\\rho \cdot \cos \theta \end{bmatrix}}$

$\mathbf {r} _{\theta }={\begin{bmatrix}\rho \cdot \cos \theta \cdot \cos \varphi \\\rho \cdot \cos \theta \cdot \sin \varphi \\-\rho \cdot \sin \theta \end{bmatrix}}$

$\mathbf {r} _{\varphi }={\begin{bmatrix}-\rho \cdot \sin \theta \cdot \sin \varphi \\\rho \cdot \sin \theta \cdot \cos \varphi \\0\end{bmatrix}}$

$E=\mathbf {r} _{\theta }^{2}=\rho ^{2};\quad G=\mathbf {r} _{\varphi }^{2}=\rho ^{2}\sin ^{2}\theta ;\quad F=\mathbf {r} _{\theta }\mathbf {r} _{\varphi }=0$

$A=\int _{\varphi =0}^{2\pi }\int _{\theta =0}^{\pi }{\sqrt {EG-F^{2}}}\mathrm {d} \theta \mathrm {d} \varphi =\int _{\varphi =0}^{2\pi }\int _{\theta =0}^{\pi }\rho ^{2}\sin \theta \mathrm {d} \theta \mathrm {d} \varphi =-\rho ^{2}\int _{\varphi =0}^{2\pi }\cos \theta |_{0}^{\pi }\mathrm {d} \varphi =2\rho ^{2}\underbrace {\int _{\varphi =0}^{2\pi }\mathrm {d} \varphi } _{2\pi }=4\rho ^{2}\pi$

Übung: Berechnen Sie die Oberfläche eines Torus (siehe dazu auch Toruskoordinaten).

Nachdem wir das Flächenelement nun mit der Parameterdarstellung ausführlich behandelt haben, wollen wir das Ganze mit kartesischen Koordinaten durchführen. Und zwar zuerst in expliziter und danach in impliziter Form.

$\mathbf {r} ={\begin{bmatrix}x\\y\\f(x,y)\end{bmatrix}}$

$\mathbf {r} _{x}={\begin{bmatrix}1\\0\\f_{x}(x,y)\end{bmatrix}}$

$\mathbf {r} _{y}={\begin{bmatrix}0\\1\\f_{y}(x,y)\end{bmatrix}}$

$\mathbf {r} _{x}\times \mathbf {r} _{y}={\begin{bmatrix}-f_{x}\\-f_{y}\\1\end{bmatrix}}$

$|\mathbf {r} _{x}\times \mathbf {r} _{y}|={\sqrt {f_{x}^{2}+f_{y}^{2}+1}}$

$\mathrm {d} \sigma ={\sqrt {f_{x}^{2}+f_{y}^{2}+1}}\;\mathrm {d} x\mathrm {d} y$

Und nun in der impliziten Form $F(x,y,z)=0$.

$\mathrm {d} F=F_{x}\mathrm {d} x+F_{y}\mathrm {d} y+F_{z}\mathrm {d} z=0$

Lösen wir z.B. $F(x,y,z)$ nach $z$ auf (vorausgesetzt, das ist möglich).

$\mathbf {r} ={\begin{bmatrix}x\\y\\f(x,y)\end{bmatrix}}$

Dafür haben wir die Ableitungen und das Vektorprodukt schon berechnet.

Es gilt: $dz=f_{x}\mathrm {d} x+f_{y}\mathrm {d} y$

Damit folgt: $\mathrm {d} F=F_{x}\mathrm {d} x+F_{y}\mathrm {d} y+F_{z}(f_{x}\mathrm {d} x+f_{y}\mathrm {d} y)=0$

$\mathrm {d} F=\underbrace {(F_{x}+F_{z}f_{x})} _{=0}\mathrm {d} x+\underbrace {(F_{y}+F_{z}f_{y})} _{=0}\mathrm {d} y=0\Rightarrow$

$f_{x}=-{\frac {F_{x}}{F_{z}}};\quad f_{y}=-{\frac {F_{y}}{F_{z}}}$

$|\mathbf {r} _{x}\times \mathbf {r} _{y}|={\sqrt {f_{x}^{2}+f_{y}^{2}+1}}={\frac {\sqrt {F_{x}^{2}+F_{y}^{2}+F_{z}^{2}}}{|F_{z}|}}$

Und somit:

$\mathrm {d} \sigma ={\frac {\sqrt {F_{x}^{2}+F_{y}^{2}+F_{z}^{2}}}{|F_{z}|}}\mathrm {d} x\mathrm {d} y$

Flächentypen

Orientierbare Flächen

Das sind alle Flächen, die eine Außen- und Innenseite aufweisen, z.B. eine Kugel-, Zylinder- oder Torusfläche.

• 
• 
• 

Nicht orientierbare Flächen

Es gibt auch Flächen, die keine eindeutigen Innen- und Außenseiten aufweisen, sogenannte einseitige Flächen. Dazu zählt das Möbiusband.

• 
• 
  August Ferdinand Möbius (1790 - 1868) deutscher Mathematiker

Siehe dazu auch  Möbiusband. Das ist nicht nur theoretisch interessant, sondern hat auch praktische Anwendungen, siehe z.B.  Möbiusband#In_der_Technik

Geschlossene Flächen

Z. B. die Kugelfläche.

Offene Flächen

Z.B. der Zylindermantel.

Zurück zu Raumkurven | Hoch zu Gesamtinhaltsverzeichnis | Vor zu Linienintegrale