MathemaTriX ⋅ Theorie. Lineare Gleichungssysteme
| ||||||||||||||||||
|
Inhalt
Ein-Aus- klappen |
| AUFGABEN |
Lineare Gleichungssysteme mit 2 Variablen
[Bearbeiten]Einsetzungsverfahren
[Bearbeiten]Wie löst man so eine Aufgabe? Man benutzt ein sogenanntes lineares Gleichungssystem. Wir werden uns hier mit der einfachste Form eines Gleichungssystems beschäftigen, einem Gleichungssystem mit zwei unbekannten und zwei Gleichungen. Es gibt verschiedene Wege so ein System zu lösen, wir werden hier zunächst einmal einen Weg zeigen.
Hier gibt es zwei unbekannte, die Anzahl der Tische für 3 Personen und die Anzahl der Tische für 5 Personen. Wenn man in Mathematik etwas nicht kennt, benutzt man ein Symbol dafür, in der Regel (kann aber a, b, z, A1, oder irgendwas sein). Lass uns dann mit die Anzahl der Tische für 3 Personen bezeichnen. Wir wissen nicht, ob die Anzahl der Tische für 5 Personen gleich so groß wie die Anzahl der Tische für 3 Personen ist. Daher müssen wir für die Anzahl der Tische für 5 Personen ein anderes Symbol benutzen, z.B. . Also:
: die Anzahl der Tische für 3 Personen
: die Anzahl der Tische für 5 Personen
Wie schon gesagt, wir wissen nicht, wie viele Tische es für 3 oder für 5 Personen gibt. Wir wissen aber schon, dass es insgesamt 8 Tische gibt. Also die x Tische und die y Tische zusammen sind 8 Tische:
Die Tische sind für 3 Personen. Wir wissen zwar nicht, wie viel ist, aber wir können sagen, dass
| 1 Tisch → | (3 · 1 =) | 3 | Personen |
| 2 Tische → | (3 · 2 =) | 6 | Personen |
| 5 Tische → | (3 · 5 =) | 15 | Personen |
| 8 Tische → | (3 · 8 =) | 24 | Personen also |
| x Tische → | (3 · x =) | Personen |
da wir x Tische haben, anstatt eine bestimmte Zahl, wie 1, 2, 5 oder 8 Tische.
In der gleichen Weise kann man sagen, dass die Tische (für 5 Personen) Gäste bedienen können.
Wir haben also Personen an den Tischen und Personen an den Tischen.
Wir wissen jetzt nicht, wie viel 3x oder 5y ist (das sind Personen), wir wissen aber, dass insgesamt 36 Personen bedient werden können, also:
Wir schreiben jetzt beide Gleichungen zusammen:
Mit einer Gleichung können wir weder x noch y finden, wir können aber hier die erste Gleichung (am einfachsten) umformen:
Da wir es wissen, dass x=8−y ist, können wir dann in der zweiten Gleichung statt x, 8−y schreiben:
(x wird also durch 8-y ersetzt)
Jetzt haben wir eine Gleichung mit einem Unbekannten. So was können wir schon lösen, wie wir beim Kapitel Umformen gelernt haben:
| |Klammer auflösen | |
| |-24 (und y zusammenrechnen) | |
| | :2 | |
y sind die Tische mit 5 Personen. Es gibt also 6 Tische für 5 Personen. Wie viele sind die restlichen? Wir benutzen unsere Gleichung:
Es gibt also x=2 Tische für 3 Personen und y=6 Tische für 5 Personen. Somit haben wir die Aufgabe gelöst!
Lineare Gleichungssysteme Begriffe
[Bearbeiten]Lass uns jetzt ein paar Begriffe erklären.
Eine Gleichung ist ein mathematischer Ausdruck, der das Symbol „=“ („ist“, „gleich“ oder „ist gleich“ ausgedrückt) zumindest einmal beinhaltet und bei dem auf beide Seiten des Symbols „=“ andere mathematische Ausdrücke stehen. „6+3=“ ist noch keine Gleichung, „6+3=9“ oder „6+3=x“ oder „6+y=x“ schon.
Wenn alle Variablen in der Gleichung ohne Hochzahl oder sonst was vorkommen, dann spricht man von einer linearen Gleichung(1). oder oder sind lineare Gleichungen. , oder hingegen nicht (letztere weil im Nenner ist).
Eine Gleichung kann keine, eine oder mehrere Variablen beinhalten. hat keine Variable (und ist allerdings eine wahre Aussage: 6+3 ist tatsächlich 9). , , haben eine Variable. , und haben zwei Variablen.
Wenn man zwei oder mehrere Gleichungen irgendwie verbindet, dann hat man ein Gleichungssystem. In diesem Kapitel haben wir 2 Gleichungen je mit 2 unbekannten gehabt:
Da beide Gleichungen hier linear sind, spricht man von einem linearen Gleichungssystem. So ein System kann man in verschiedenen Wege lösen. Der Weg, den wir hier benutzt haben, nennt man Einsetzungsverfahren. Es gibt dann noch das Gleichsetzungsverfahren und das Additionsverfahren (wir werden sie gleich lernen). Das Einsetzungsverfahren ist sehr wichtig (auch in anderen Wissenschaften, wie in der Physik), da man es leicht auch bei nicht lineare Gleichungssysteme anwenden kann. Dieses Thema ist von einem höheren Niveau und daher nicht in diesem Buch behandelt.
Die Zahlen (manchmal aber auch Symbole), die vor den Variablen stehen und mit diesen multipliziert werden, nennt man Koeffizienten. In der zweiten Gleichung () ist der Koeffizient von 3 und von 5. In der ersten Gleichung () steht keine Zahl vor den Variablen. Trotzdem sagt man dann, dass der Koeffizient 1 ist (es gilt ja, dass und ist). Bei ist der x-Koeffizient , der y-Koeffizient und der z-Koeffizient . Die Symbole c und d sind in dieser Gleichung nicht Variablen (das ist aber nicht immer klar, man soll in solchen Fällen immer die Vorgaben lesen). Wenn ein Symbol benutzt wird, der eine feste Zahl (und daher keine Variable) darstellt, dann nennt man diese Symbol eine Konstante. Die Konstante c ist hier gleichzeitig der Koeffizient der Variablen v. Die Konstante d hingegen ist keiner Koeffizient.
Ein Gleichungssystem kann keine, zwei oder unendlich viele Lösungen haben. Das ist allerdings Thema eines anderen Kapitels.
Gleichsetzungsverfahren
[Bearbeiten]
Formen wir beide Gleichungen auf um:
- Die erste Gleichung geht leicht:
daher
- Die zweite Gleichung ist etwas schwerer:
| |-5y | |
| |:3 | |
Das Gleichungssystem sieht jetzt wie in Folgendem aus:
Da beide Ausdrücke rechts der beiden Gleichungen gleich mit sind, sind sie auch zueinander gleich:
Jetzt haben wir eine Gleichung mit einer Unbekannte, was man mit Umformen lösen kann:
| |⋅3 | |
| |(Klammer auflösen) | |
| |−36+3y | |
| |:(−2) | |
und daher
Die Antwort ist:
und
also genau wie vorher, wie es zu erwarten war.
Additionsverfahren
[Bearbeiten]
Nehmen wir hier die Variable (man kann aber genauso die Variable benutzen). Der y-Koeffizient in der ersten Gleichung ist 3 und in der zweiten 2. Wenn wir den ersten Koeffizient mit 2 multiplizieren und den zweiten mit -3 bekommen wir 6 und ihre Gegenzahl -6. Wenn wir beide Seiten der ersten Gleichung mit 2 multiplizieren, dann haben wir auf beiden Seiten das Gleiche gemacht und beide Seiten werden weiter gleich bleiben (siehe Gegenrechnungen). Ebenfalls wenn wir beide Seiten der zweiten Gleichung mit -3 multiplizieren, bleiben beide Seiten dieser Gleichung gleich:
Wenn wir jetzt die Summe der linken Seiten und die Summe der rechten Seiten beider Gleichungen berechnen, werden die Ergebnisse gleich sein:
Zauberei! Jetzt haben wir nur eine Gleichung mit einem Unbekannten, die wir sofort lösen können!
Wenn wir jetzt eine der beiden Anfangsgleichungen nehmen, können wir auch y berechnen. Nehmen wir die erste:
(x ist -2, wie wir gerade berechnet haben)
|+4
|:3
Die Lösung des Gleichungssystems lautet daher:
und
Tatsächlich kann man diese Werte in beiden Gleichungen einsetzen und feststellen, dass das Ergebnis stimmt. Ersetzen wir in beiden Gleichungen x durch -2 und y durch 5, dann bekommen wir eine wahre Aussage:
Es gibt kein anderes Zahlenpaar, der beide Gleichungen richtig löst, also die Lösung ist eindeutig! Ist es aber immer so? Das ist das Thema des nächsten Unterkapitels.
Graphische Lösung eines linearen Gleichungssystems
[Bearbeiten]Im Kapitel über lineare Funktionen wird erklärt, wie man in einem Koordinatensystem eine lineare Funktion mit Hilfe von zwei Punkten zeichnen kann (zwei Punkte sind eine hinreichende und notwendige Voraussetzung, um eine lineare Funktion zu definieren; daher reichen zwei Punkte um die Funktion zu zeichnen). Nehmen wir die erste Funktion vom folgendem Gleichungssystem:
| (Funktion A) | |
| (Funktion B) |
-
Funktion A
-
Funktion B
-
Funktion A und B
Man kann zwei Punkte für die Funktion finden, indem man willkürlich Werte für x angibt und die entsprechenden Werte für y findet. Für ist:
→ → → .
Für ist:
→ → → .
Wir haben also zwei Punkte der Funktion A: und . Diese Punkte können wir dann im Koordinatensystem zeichnen und auch die Gerade, die der Funktion entspricht, wie im Bild „Funktion A“.
Entsprechend kann man Punkte für die Funktion B finden. Für ist:
→ → → → .
Für ist :
→ → → → .
Wir haben also zwei Punkte der Funktion B: und . Diese Punkte können wir dann im Koordinatensystem zeichnen und auch die Gerade, die der Funktion entspricht, wie im Bild „Funktion B“.
Wenn wir jetzt beide Funktionen in einem Koordinatensystem zeichnen, dann bekommen wir das Bild „Funktion A und B“. Da kann man klar sehen, dass die Funktionen einander an einem einzigen Punkt schneiden, den Punkt . Dieser Punkt ist die Lösung des Gleichungssystems der Funktionen A und B. Leider kann man i.d.R. den - und den -Wert nicht genau ablesen, daher ist diese Methode nicht so genau, wie die drei Verfahren der vorherigen Absätzen.
Lösungsmenge eines linearen Gleichungssystems
[Bearbeiten]| Gleichungssystem A | Gleichungssystem B | |
|---|---|---|
Die Lösung des ersten linearen Gleichungssystems war und , des zweitens und . Geht es aber immer, dass ein Gleichungssystem eine Lösung hat? Die Antwort ist nein. Probieren wir das folgendes Gleichungssystem mit dem Einsetzungsverfahren zu lösen:
| Gleichungssystem C |
|---|
Lösung
→
→ → → !
Man sagt, dass die Aussage am Ende falsch ist. ist doch nicht gleich ! Das bedeutet, dass die beiden Gleichungen, die wir im Gleichungssystem haben ( und ), nicht gleichzeitig erfüllt werden können. Man sagt, dass das Gleichungssystem keine Lösung hat.
Es gibt allerdings noch eine Möglichkeit. Das Gleichungssystem kann unendlich viele Lösungen haben, wie im folgenden Beispiel:
| Gleichungssystem D |
|---|
Lösung
→
→ → →
Man sagt, dass die Aussage am Ende immer wahr ist. Egal wie viel ist, die beiden Gleichungen werden immer gelten. Man soll doch etwas vorsichtig sein. Wenn ist, dann ist (erste Gleichung → → → ). Wenn ist, dann ist (erste Gleichung → → → ). Für jedes gibt es ein bestimmtes und umgekehrt.
Allerdings gilt genau das Gleiche in der zweiten Gleichung: Wenn ist, ist ( → → → ). Wenn ist, dann ist ( → → → ). Egal welchen Wert man für benutzt, wird es für beide Gleichungen der gleiche Wert für als Lösung gelten (und umgekehrt). Es gilt nicht, dass alle Wertepaare (alle Punkte auf der Ebene) Lösungen des Gleichungssystems sind, sondern dass alle Lösungen der einen Gleichung auch Lösungen der anderen Gleichung sind.
Das war allerdings nicht der Fall, als wir eine Lösung des Gleichungssystems hatten (und auf gar keinen Fall, als wir keine Lösung hatten). Nehmen wir beispielsweise das Gleichungssystem A:
6
Da haben wir als Lösung und gefunden. Diese Lösung gilt gleichzeitig für beide Gleichungen. Tatsächlich wenn ist, dann gilt für die erste Gleichung ( → → →) aber auch für die zweite Gleichung ( → → →) . Wenn aber , dann gilt für die erste Gleichung ( → → →) . Für die zweite Gleichung hingegen gilt in diesem Fall: ( → → →) . Die beiden Gleichungen haben den gleichen Wert für y(den Wert 6), nur wenn ist. Man sagt, dass Gleichungssystem A und B eine Lösung haben, Gleichungssystem C keine und Gleichungssystem D unendlich viele Lösungen haben.
Ein lineares Gleichungssystem kann keine, eine oder unendlich viele Lösungen haben.
Viel besser kann man das Ganze verstehen, wenn man die graphischen Lösungen betrachtet.
-
Gleichungssystem A
-
Gleichungssystem B
-
Gleichungssystem C
-
Gleichungssystem D
Im Gleichungssystem A gibt es nur ein Wertepaar, das für beide Funktionen stimmt: . Wenn ist, dann ist für beide Funktionen. Für jeden anderen Wert von x stimmt der Wert von y nicht mehr überein. Beispielsweise für ist für die Funktion und für die Funktion . Es gibt nur ein Wertepaar, das für beide Funktionen eine Lösung ist, und dieses Wertepaar (also der Punkt ) ist die Lösung des Gleichungssystems.
Entsprechend hat auch das Gleichungssystem B nur eine Lösung, den Punkt (Wertepaar) , wie man eindeutig im entsprechenden Bild auch sehen kann. Das ist allerdings nicht der Fall für das Gleichungssystem C. Da laufen die Darstellungen der Funktionen im Koordinatensystem (die Geraden sind) parallel zueinander, sie treffen einander nie. Sie haben daher keinen gemeinsamen Punkt und das Gleichungssystem hat daher keine Lösung (man sagt, dass die Lösung die leere Menge ist). Im Gleichungssystem D hingegen sind alle Punkte der einen Funktion auch Punkte der anderen. Alle Wertepaare, die zu diesen Funktionen gehören, sind daher auch Lösungen des Gleichungssystems D. Das System hat somit unendlich viele Lösungen. Beide Funktionen sind in diesem Fall unterschiedliche Darstellungen der gleichen Funktion. Tatsächlich, wenn man beide Seiten der zweiten Funktion (des Systems D) durch 3 dividiert, bekommt man die erste Funktion:
.
Lösbarkeit eines linearen Gleichungssystems mit 2 Variablen
[Bearbeiten]Man soll zuerst beide Gleichungen in die sogenannte explizite Form umformen, also in der Form, in der y allein auf der linken Seite steht. Nehmen wir die Gleichungssysteme A, C und D des vorherigen Absatzes:
| Gleichungssystem A | Gleichungssystem C | Gleichungssystem D | ||
|---|---|---|---|---|
In der expliziten Form sehen diese Systeme wie im Folgenden aus:
| Gleichungssystem A | Gleichungssystem C | Gleichungssystem D | ||
|---|---|---|---|---|
Bei System A ist die Steigung unterschiedlich (-1 in der ersten Gleichung und -0,6 in der zweiten).
Wenn die Steigung der beiden linearen Funktionen unterschiedlich ist, dann hat das System mit Sicherheit genau eine Lösung.
Bei den Systemen C und D ist die Steigung überall die Gleiche (). Im System C haben die Gleichungen einen anderen y-Achsenabschnitt (+4 und +2). Im System D ist hingegen auch der y-Achsenabschnitt der beiden Gleichungen der gleiche (+4)
Wenn die Steigung der beiden linearen Funktionen die gleiche ist, gibt es zwei Möglichkeiten:
- Ist der y-Achsenabschnitt unterschiedlich, dann gibt es keine Lösung.
- Ist der y-Achsenabschnitt der gleiche, dann gibt es unendlich viele Lösungen.
Textaufgaben linearer Gleichungssysteme mit 2 Variablen
[Bearbeiten]In einem Café gibt es 8 Tische. Manche sind für 3 Personen und der Rest für 5 Personen. Insgesamt kann das Café 36 Personen bedienen. Wie viele 3 bzw. 5 Personen-Tische gibt es im Café?
Schauen wir die Denkweise genauer an. Die Anzahl der Tische ist bekannt, als auch die der Personen insgesamt. Was ist hier unbekannt (und letztendlich auch gefragt)? Wie viele Tische für 5 Personen und wie viele für 3 Personen es gibt. Für die Unbekannten in jedem mathematischem Problem benutzt man irgendwelche Symbole. Wir haben x und y benutzt, dass könnte aber genauso a und b, oder m und n, oder f und d oder irgendwas anders sein. Wichtig: Es gibt zwei Unbekannte, wir müssen also zwei verschiedenen Symbole dafür benutzen. Wenn es drei Unbekannte gibt, dann soll mal drei unterschiedlichen Symbole benutzen usw. (wie werden uns aber hier nur mit Gleichungssystemen mit zwei Unbekannten beschäftigen).
Am Anfang muss man definieren, was jedes Symbol darstellt. In dieser Aufgabe haben wir gesagt, dass die Tische für 3 Personen und y die Tische für 5 Personen sind:
x: die Tische für 3 Personen
y: die Tische für 5 Personen
Dieser Schritt sollte nicht so schwer sein. Man gibt einfach Namen (Symbole) für die unbekannten Sachen. Beim nächsten Schritt haben viele Menschen die größten Schwierigkeiten. Dabei ist die Sache nicht wirklich so schwer. Man soll das Problem vorsichtig lesen und den Text in die mathematische Sprache umsetzen. Dafür muss man nicht den ganzen Text verstehen, sondern auf Schlüsselworte beachten. In dieser Aufgabe steht, dass es 8 Tische gibt. Auch wenn man nicht wüsste, was ein Tisch ist, kann man schon schreiben, dass die Tische zusammen 8 sind. Welche Rechenart steht in Mathematik für zusammen? Die Addition. Also:
x+y=8
Wir haben zwei Unbekannte, also wir brauchen zwei Gleichungen, um die Aufgabe eindeutig zu lösen. Die zweite Gleichung zu erzeugen war in dieser Aufgabe nicht so leicht. Wir haben gesagt: Wenn es 2 Tische für 3 Personen gibt, dann sitzen an diesen Tischen 2⋅3=6 Personen, es 5 Tische für 3 Personen gibt, dann sitzen an diesen Tischen 5⋅3=15 Personen usw. Man merkt, dass damit wir die Personen berechnen, die Anzahl der Tische mit der Anzahl der Personen pro Tisch (hier 3 Personen pro Tisch) multiplizieren müssen. Wir wissen aber nicht, wie viele Tische für drei Personen es gibt. Wir haben aber doch ein Symbol dafür benutzt: das sind x Tische. Dieses Symbol muss man also mit der Anzahl der Personen pro Tisch (hier 3) multiplizieren, um durch einen Term zu zeigen, wie viele Personen an diesen Tischen sitzen können: 3x! Dass ist (noch) nicht eine bestimmte Zahl, das sind aber doch die Personen die an diesen x Tischen sitzen können. Entsprechend können an den y Tischen für 5 Personen insgesamt 5y Personen sitzen (Anzahl der Tische y mal Personen pro Tisch, hier 5). In der Aufgabe steht, dass das Café insgesamt 36 Personen bedienen kann. Also die Anzahl der Personen, die an den zwei Tischkategorien (eine Kategorie die 3-Personen Tische, zweite Kategorie die 5-Personen Tische) sitzen können ist insgesamt 36 Personen. Welche Rechenart wird hier angedeutet? Wieder Addition. Die Personen der beiden Kategorien zusammen (also plus) sind 36:
3x+5y=36
Wir haben also zwei Gleichungen und zwei Unbekannte.
x+y=8
3x+5y=36
Jetzt kann man eine der dargestellten Wege benutzen, um x und y herauszufinden. In unserem Beispiel haben wir das Ersetzungsverfahren benutzt.
Erzeugen wir das Gleichungssystem für noch ein paar Textaufgaben:
Iris ist 2,5 mal älter als ihr Bruder Andreas. Zusammengezählt sind ihre Altersjahren 14. Wie viele Jahren alt sind die beiden Geschwister?
Gefragt sind die Lebensalter der beiden Geschwister. Wir schreiben mit i das Lebensalter von Iris und mit a von Andreas. Iris ist 2,5 mal älter und zusammen sind die Jahre 18:
i=2,5⋅a und i+a=14
Dieses System lässt sich sehr leicht durch das Ersetzungsverfahren lösen. Wir ersetzen i in der zweiten Gleichung durch 2,5a (da i=2,5a, wie es schon in der ersten Gleichung steht):
i+a=18 → 2,5a+a=14 → 3,5a=14 (:3,5) → a=4 und sofort i=2,5a=2,5⋅4 → i=10 (also tatsächlich i+a=14)
Die Summe des Fünffachen einer Zahl und 4 ist so viel wie eine andere Zahl um 1 reduziert. Die Differenz des dreifachen der zweiten Zahl und 43 ist so viel wie die erste Zahl um 14 erhöht. Berechnen sie die Zahlen.
Viele finden solche Aufgaben extrem schwer. Dabei muss man einfach Schritt für Schritt vorgehen. Erst gibt man Symbole für die zwei unbekannten Zahlen.
e ist die erste Zahl
z ist die zweite Zahl
Gehen wir Schritt für Schritt vor:
Die Summe des Fünffachen einer Zahl.... Die erste Zahl haben wir e genannt. Das fünffache bedeutet 5e. Über die Summe wissen wir noch nichts, außer dass der erste Summand 5e sein wird.
Die Summe des Fünffachen einer Zahl und 4.... Hier erkennen wir den zweiten Summand: 4. Also bisher haben wir: 5e+4
Die Summe des Fünffachen einer Zahl und 4 ist so viel wie.... ...ist so viel wie in der mathematische Sprache umgesetzt ist nichts mehr und nichts mehr als das Symbol für gleich (=). Also bisher haben wir: 5e+4=
Die Summe des Fünffachen einer Zahl und 4 ist so viel wie eine andere Zahl um 1 reduziert. Die zweite (die "andere") Zahl haben wir z genannt und sie wird um 1 reduziert also z−1. Bisher haben wir: 5e+4=z−1 Hier endet der erster Satz. Wir haben also schon unsere erste Gleichung!
5e+4=z-1
Fangen wir jetzt mit dem zweiten Satz an: Die Differenz des dreifachen der zweiten Zahl.... Über die Differenz kenne wir nur den Minuend. Er ist das dreifache der zweiten Zahl. Die zweite Zahl haben wir z genannt, also ist ihr Dreifaches 3z. Bisher haben wir daher: 3z−...
Die Differenz des dreifachen der zweiten Zahl und 43 Jetzt haben wir auch den Subtrahend der Differenz: 3z−43
Die Differenz des dreifachen der zweiten Zahl und 43 ist so viel wie ...ist so viel wie bedeutet ist gleich: 3z−43=
Die Differenz des dreifachen der zweiten Zahl und 43 ist so viel wie die erste Zahl um 14 erhöht Die erste Zahl ist e und sie wird um 14 erhöht (also plus 14): 3z−43=e+14. Wir haben jetzt auch die zweite Gleichung! Das Gleichungssystem lautet:
5e+4=z−1
3z−43=e+14
Dieses System kann man dann mit einem der präsentierten Verfahren lösen. Die Antwort ist e=3 und z=20, wie man überprüfen kann:
5⋅3+4=20−1 ✔ und
3⋅20−43=3+14 ✔
Viele Menschen denken, dass solche Aufgaben schwer wären. Wie man hier sieht, wenn man die Aufgabe Schritt für Schritt löst, ist es nicht so schwer. Das braucht einfach etwas Konzentration, ist aber durchaus fast für jeden möglich.
In einer Flups gibt es 37 Tröpats. Manch davon haben 4 Hupals, die restlichen 7 Hupals. Die Flups beihaltet damit 190 Hupals. Wie viele Tröpats mit 4 bzw. 7 Hupals gibt es?
Man mag hier fragen, was zum Teufel Flups, Tröpats und Hupals sind. Meine Antwort ist dann eine weitere Frage: Ist diese Kenntnis für die Lösung der Aufgabe notwendig? Die Antwort ist ganz einfach NEIN! Wenn in einer Prüfungssituation jemand eine unbekanntes Wort trifft, soll man erst entscheiden, ob dieses Wort für die Lösung wichtig ist, sonst verliert man Zeit, die für eine Prüfung i.d.R. sehr wichtig ist. Ziel dieser Aufgabe ist darauf aufmerksam zu machen. In der Aufgabe wird NICHT gefragt, was Flups usw sind. Ḿan braucht es daher auch nicht wissen. Wichtig sind nur Schlüsselworte und -phrasen, wie z.B. In... gibt es, was darauf hinweist, dass die Tröpats insgesamt 37 sind. Der erste Schritt ist für jede Unbekannte ein Symbol einzusetzen. Wenn v die Tröpats mit 4 Hupals sind und s die Tröpats mit 7 Hupals, dann haben wir die erste und die zweite Gleichung, genau wie im ersten Beispiel in diesem Teilkapitel:
v+s=37
4v+7s=190
Das System kann man dann in einer beliebige Weise lösen. Die Antwort ist 23 Tröpats mit 4 Hupals und 14 Tröpats mit 7 Hupals (was das auch immer sein könnte ![]() ).
).
Lineare Gleichungssysteme mehrerer Variablen
[Bearbeiten]Das gaußsche Eliminationsverfahren
[Bearbeiten]Als linear wird eine Gleichung bezeichnet, wenn alle in ihr vorkommenden Variablen nur mit der Hochzahl 1 vorkommen. Beispielsweise ist eine lineare Gleichung, da alle Variablen (x, d und m) ohne Hochzahl, also mit der Hochzahl 1 vorkommen. Die Gleichung ist linear, was die Variablen x und m betrifft, nicht aber was die Variablen d und c betrifft. Die Gleichung ist nicht linear.
Ein lineares Gleichungssystem besteht aus mehreren linearen Gleichungen mit mehreren Variablen. Eine, eindeutige Lösung für so ein System, gibt es, wenn es möglich ist, jede Variable durch jeweils eins Zahl zu ersetzen, so dass alle Gleichungen stimmen. In der Regel wird es in den Aufgaben so viele Gleichungen wie Variablen geben, das muss aber nicht sein. Betrachten wir zunächst einmal ein Beispiel mit 2 Variablen und 2 Gleichungen:
Es gibt zumindest 4 Wege, dieses System zu lösen: graphisch (was ohne Computer ungenau ist) und mit dem Gleichsetzungs-, Einsetzungs- und Additionsverfahren.
- Graphisch
Beide lineare Funktionen mit Hilfe von jeweils 2 Punkten abzeichnen:
|
Der Schnittpunkt L:(2|6) der beiden Geraden ist die Lösung
- Mit dem Gleichsetzungsverfahren
- Mit dem Einsetzungsverfahren
- Mit dem Additionsverfahren
Wenn am Anfang neben der zweiten Gleichung geschrieben wird, ist damit gemeint, das von jeder Seite in der zweiten Gleichung 3 mal die entsprechende Seite der ersten Gleichung subtrahiert wird. Dadurch wird in der zweiten Gleichung die x Variable wegfallen ().
Das Gleichsetzungsverfahren benutzen wir oft, wenn wir die Schnittpunkte zweier Funktionen finden wollen (also die Lösung des entsprechenden oft nicht linearen Gleichungssystems). Des Ersetzungsverfahren wird oft in Physik und anderen Wissenschaften benutzt, wenn mehrere Formel nacheinander benutzt werden müssen. Für die Lösung allerdings von linearen Gleichungssystemen mit 3 oder mehreren Variablen wird fast ausschließlich ein das gaußsche Verfahren benutzt, das dem Additionsverfahren sehr ähnelt. Nehmen wir folgendes Beispiel eines LGS mit 3 Variablen und 3 Gleichungen:
Es ist übersichtlicher, nur die Koeffizienten der Variablen a, b und c in einer sogenannten "Matrix" zu schreiben. Jede Spalte der Matrix entspricht einer Variable: in der ersten Spalte sind die Koeffizienten von a, in der zweiten von b und in der dritten von c. Separat in einer Spalte rechts werden die rechten Seiten der Gleichungen geschrieben (die keine Koeffizienten sind).
Die Matrix kann mit elektronischen Hilfsmitteln
oder mit dem gaußschen Verfahren gelöst werden.
Ziel des Verfahrens ist, durch Addition und Subtraktion
von Vielfachen der verschiedenen Zeilen folgende
("diagonale") Form der Matrix zu erreichen:
Die erste Spalte ist für die Variable a, die zweite für
die Variable b und die dritte für die Variable c. Als
lineares Gleichungssystem wird daher die letzte
Matrize wie im Folgenden dargestellt:
was gleichbedeutend ist, wie:
Das bedeutet wiederum, dass wir die Lösung
des LGS in der diagonalen Matrize sofort ablesen können.
Schauen wir den ganzen Prozess mit Hilfe des Beispiels. Bei
jedem Schritt soll noch eine Koeffizient null werden, bis wir
die Diagonale Form erreichen.
|
|
|
|
|
|
|
|
|
|
Wir haben vereinbart, dass die dritte Spalte die c-Koeffizienten beinhaltet. Die erste Zeile in der letzten Matrize zeigt uns dann:
Entsprechend für die zweite und dritte Spalte:
Somit haben wir eine eindeutige Lösung für dieses LGS gefunden. Wenn wir die Lösungen für a, b und c in den Anfangsgleichungen einsetzen, werden alle drei Gleichungen stimmen. Wenn wir andere Zahlen dafür benutzen, werden die drei Gleichungen nicht mehr (gleichzeitig) stimmen.
Dieses Verfahren ist das einfachste, wenn wir ein LGS mit 3 oder mehreren Variablen lösen wollen, daher wird es auch bei mehreren Variablen benutzt.
Textaufgaben zu linearen Gleichungssystemen
[Bearbeiten]|
Eine Bootverleihfirma hat insgesamt 43 Boote, |
Hier sind drei Sachen gefragt: die Anzahl der Tretboote, die Anzahl der Ruderboote und die Anzahl der Kanus. Schreiben wir t für die Anzahl der Tretboote, r für die Ruderboote und k für die Kanus (selbstverständlich können wir auch andere Symbole benutzen, z.B. a, b und c usw.). Versuchen wir jetzt die Angabe in die mathematische Sprache zu "übersetzten".
- Nach Angabe sind alle Boote zusammen 43. Wenn wir die Boote zusammenrechnen (addieren) wird daher das Ergebnis 43 sein. Wir müssen also die Symbole für die Anzahl der verschiedenen Bootarten addieren:
- Allerdings kann die Firma höchstens 159 Personen bedienen. Wenn alle Tretboote (t) unterwegs sind, dann sind in diesen Booten 5t Personen, für die Ruderboote sind es 3r Personen und für die Kanus 2k Personen. Allesamt gilt daher für die Personen, die die Firma höchstens bedienen kann:
- Die Firma verdient 8 €/h für jedes der t Tretboote, also für alle zusammen 8·t €/h. Entsprechend sind die Einnahmen pro Stunde für die Ruderboote 7r € und für die Kanus 4k €. Daher gilt für die maximalen Einnahmen der Firma (pro Stunde), die laut Angabe 271 € sind:
Schreiben wir die drei Gleichungen, die wir durch die "Übersetzung" des Textes erzeugt haben, als ein Gleichungssystem auf:
|
|
Dieses LGS können wir mit Hilfe eines elektronischen Mittels lösen. Wenn keines vorhanden ist, dann können wir am einfachsten das gaußsche Eliminationsverfahren benutzten:
|
|
Die dritte Spalte ist die Anzahl der Kanus, die zweite die Anzahl der Ruderboote und die erste die Anzahl der Tretboote.
Es gibt daher 24 Tretboote, 1 Ruderboot und 18 Kanus.
































































































































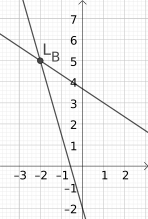


































![{\displaystyle \left[{\begin{matrix}9&3&1\\2{,}25&1{,}5&1\\4&2&0\end{matrix}}\left|{\begin{matrix}5\\4{,}5\\0\end{matrix}}\right.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e18390e2731f54e621fba0f9005555af0115614)
![{\displaystyle \left[{\begin{matrix}1&0&0\\0&1&0\\0&0&1\end{matrix}}\left|{\begin{matrix}\textstyle {L_{a}}\\\textstyle {L_{b}}\\\textstyle {L_{c}}\end{matrix}}\right.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0bb8f6580fd09bd0c2f745438fb0191be185e9)



![{\displaystyle \left[{\begin{matrix}9&3&1\\2{,}25&1{,}5&1\\4&2&0\end{matrix}}\left|{\begin{matrix}5\\4{,}5\\0\end{matrix}}\right.\right]{\begin{matrix}\textstyle {\frac {\qquad }{}}\\I-II\\\textstyle {\frac {\qquad }{}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5efec2cb32ec2cf47220af9b3fe24c2a1b83cf9)






![{\displaystyle \left[{\begin{matrix}9&3&1\\6{,}75&1{,}5&0\\4&2&0\end{matrix}}\left|{\begin{matrix}5\\0{,}5\\0\end{matrix}}\right.\right]{\begin{matrix}\textstyle {\frac {\qquad }{}}\\\textstyle {\frac {\qquad }{}}\\{4\,II-3\,III}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/555940a7b8a02e3e9335379a6e6f9b10db95ec5b)
![{\displaystyle \left[{\begin{matrix}9&3&1\\6{,}75&1{,}5&0\\15&0&0\end{matrix}}\left|{\begin{matrix}5\\0{,}5\\2\end{matrix}}\right.\right]{\begin{matrix}\textstyle {\frac {\qquad }{}}\\II\,-0{,}45\,III\\:15\qquad \qquad \end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c49c925d8595d992dc332be21c7987d739a5d1b7)
![{\displaystyle \left[{\begin{matrix}9&3&1\\0&1{,}5&0\\1&0&0\end{matrix}}\left|{\begin{matrix}5\\-0{,}4\\\textstyle {\frac {2}{15}}\end{matrix}}\right.\right]{\begin{matrix}-2\,II-9\,III\\:1{,}5\qquad \qquad \\\textstyle {\frac {\qquad }{}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46d71bfe49235220a236a90c2b1a762514a3dd5a)
![{\displaystyle \left[{\begin{matrix}0&0&1\\0&1&0\\1&0&0\end{matrix}}\left|{\begin{matrix}\textstyle {\frac {23}{5}}\\\textstyle {-{\frac {4}{15}}}\\\textstyle {\frac {2}{15}}\end{matrix}}\right.\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b22be5fe05d5281549c8d41e2e3f12b60707144)
















